
题目列表(包括答案和解析)
4.闭区间上的二次函数的最值
二次函数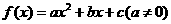 在闭区间
在闭区间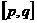 上的最值只能在
上的最值只能在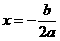 处及区间的两端点处取得,具体如下:
处及区间的两端点处取得,具体如下:
当a>0时,若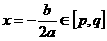 ,则
,则
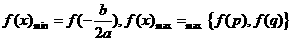 ;
;
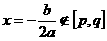 ,
,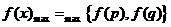 ,
,
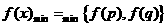 .
.
当a<0时,若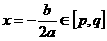 ,则
,则
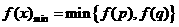 ,若
,若
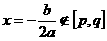 ,则
,则
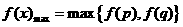 ,
,
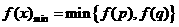 .
.
3.方程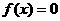 在
在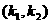 上有且只有一个实根,与
上有且只有一个实根,与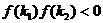 不等价,前者是后者的一个必要而不是充分条件.特别地,
方程
不等价,前者是后者的一个必要而不是充分条件.特别地,
方程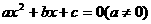 有且只有一个实根在
有且只有一个实根在
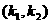 内,等价于
内,等价于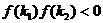
2..解连不等式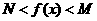
1.二次函数的解析式的三种形式
(1)一般式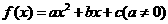 ;
;
(2)顶点式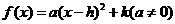 ;
;
(3)零点式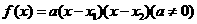 .
.
(1)了解映射的概念,理解函数的概念.
(2)了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法.
(3)了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数.
(4)理解分数指数幂的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图像和性质.
(5)理解对数的概念,掌握对数的运算性质.掌握对数函数的概念、图像和性质.
(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题.
3.解答题(有6小题,共80分)
(15) (12分)已知线段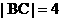 , BC的中点为M , 点A与B、C两点的距离之和为6, 设
, BC的中点为M , 点A与B、C两点的距离之和为6, 设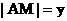 ,
, 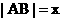 , 求
, 求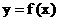 的函数表达式及其定义域.
的函数表达式及其定义域.
(16)(12分)已知二次函数f (x )的二次项系数是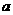 ,且不等式
,且不等式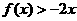 的解集为
的解集为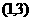 .(1)若方程
.(1)若方程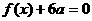 有两个相等的实根,求f
(x )的解析式;(2)若f (x )的最大值为正数,求
有两个相等的实根,求f
(x )的解析式;(2)若f (x )的最大值为正数,求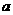 的取值范围.
的取值范围.
(17)(14分)设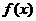 是
是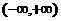 上的奇函数,对任意实数x,都有
上的奇函数,对任意实数x,都有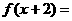
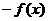 ,当
,当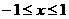 时,
时,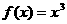 。(1)试证:
。(1)试证: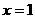 是函数
是函数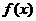 的一条对称轴;(2)证明函数
的一条对称轴;(2)证明函数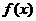 是以4为周期的函数,并求
是以4为周期的函数,并求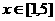 时,
时,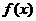 的解析式.
的解析式.
(18)(14分)预计某地区明年从年初开始的前x个月内,对某种商品的需求总量f(x)(万件)与月份x的近似关系为f(x)=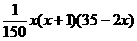 (x∈N
(x∈N 且x≤12).(1)写出明年第x个月的需求g(x)(万件)与月份x的函数关系式,并求出哪个月份的需求量超过1.4万件;(2)如果将该商品每月都投放市场P万件,要保证每月都满足供应,P应至少为多少万件?
且x≤12).(1)写出明年第x个月的需求g(x)(万件)与月份x的函数关系式,并求出哪个月份的需求量超过1.4万件;(2)如果将该商品每月都投放市场P万件,要保证每月都满足供应,P应至少为多少万件?
(19)(14分)(07宁夏)设函数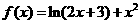 。(Ⅰ)讨论
。(Ⅰ)讨论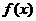 的单调性;
的单调性;
(Ⅱ)求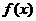 在区间
在区间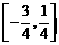 的最大值和最小值.
的最大值和最小值.
(20)(14分)现有一批货物由海上从A地运往B地,已知货船的最大航行速度
为35海里/小时,A地至B地之间的航行距离约为500海里,每小时的运输成本
由燃料费和其余费用组成,轮船每小时的燃料费用与轮船速度的平方成正比(比
例系数为0.6),其余费用为每小时960元. (1)把全程运输成本y(元)表示为
速度x(海里/小时)的函数; (2)为了使全程运输成本最小,轮船应以多大速
度行驶?
2.填空题(每小题5分,共20分)
(11)(07宁夏)设函数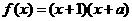 为偶函数,则
为偶函数,则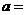 .
.
(12)(07广东)函数 的单调递增区间是 .
的单调递增区间是 .
(13)(07山东)设函数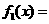
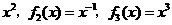 ,则
,则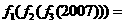 .
.
(14)(07山东)函数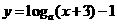
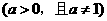 的图象恒过定点
的图象恒过定点 ,若点
,若点 在直线
在直线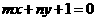 上,其中
上,其中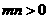 ,则
,则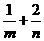 的最小值为
.
的最小值为
.
1.选择题(每小题5分,共50分)
(1)(07广东)已知集合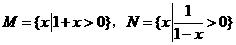 ,则
,则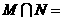 ( )
( )
A.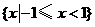 B.
B.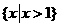 C.
C.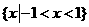 D.
D.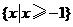
(2)(07广东)若函数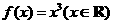 ,则函数
,则函数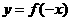 在其定义域上是( )
在其定义域上是( )
A.单调递减的偶函数 B.单调递减的奇函数
C.单调递增的偶函数 D.单调递增的奇函数
(3)(07山东)给出下列三个等式: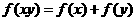 ,
,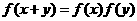 ,
, 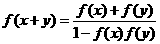 ,下列函数中不满足其中任何一个等式的是( )
,下列函数中不满足其中任何一个等式的是( )
A.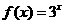 B.
B.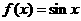 C.
C.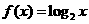 D.
D.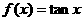
(4)已知函数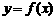 (
( )满足
)满足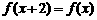 ,且当
,且当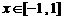 时,
时,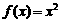 ,则
,则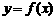 与
与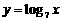 的图像的交点的个数为( )
的图像的交点的个数为( )
A.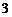 B.
B.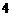 C.
C.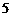 D.
D.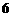
(5)设函数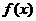 是定义在
是定义在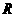 上的以3为周期的奇函数,若
上的以3为周期的奇函数,若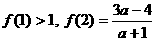 ,则a 的取值范围是
( )
,则a 的取值范围是
( )
A.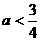 B.
B.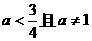 C.
C.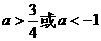 D.
D.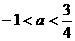
(6)设y=f (x)是定义在R上的奇函数, 当x≥0时, f (x)=x 2-2 x, 则在R上f (x)的表达式为 ( )
A. 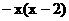 B.
B. 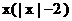 C.
C. 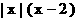 D.
D. 
(7) 二次函数f (x )满足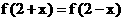 , 又f (x)在
, 又f (x)在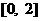 上是增函数, 且f(a)≥f(0), 那么实数a的取值范围是
( )
上是增函数, 且f(a)≥f(0), 那么实数a的取值范围是
( )
A. a≥0 B. a≤0 C. 0≤a≤4 D. a≤0或a≥4
(8) 函数y=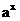 在
在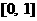 上的最大与最小值的和为3, 则a等于 ( )
上的最大与最小值的和为3, 则a等于 ( )
A. 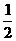 B.
2
C. 4 D.
B.
2
C. 4 D.
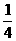
(9)若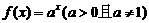 的反函数
的反函数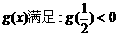 ,则函数
,则函数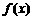 的图像向左平移一个单位后的图像大致是下图中的 ( )
的图像向左平移一个单位后的图像大致是下图中的 ( )
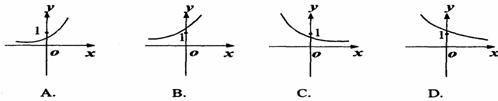
(10)若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法计算,其参考数据如下
|
f(1)=-2 |
f(1.5)=0.625 |
f(1.25)= -0.984 |
|
f(1.375)= -0.260 |
f(1.4375)=0.162 |
f(1.40625)= -0.054 |
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为
A.1.2 B.1.3 C.1.4 D.1.5
4.逐点落实,提高训练的有效性。要重视提高教育教学效率,重视训练的
有效性和质量,反对耗时费力的题海战术。按照课标要求,将知识点分为三个层面,精讲巧练,逐点落实,这三个方面是:一个是知识点的逐点落实,放在第一轮复习时解决,要求考点全部过关,另一个是题型的逐点落实,并确定各类题型(选择题、填空题、解答题)的过关标准;第三是数学方法的逐点落实,要把主要数学方法归纳总结,要求主要的数学方法要牢固掌握,熟练应用。
3.明确目标,增强训练的有效性。在巩固夯实基础的系统复习结束后,要重点进行解答题的解题训练,针对不同难度的试题,要求不同。数学考卷中有六道解答题,前两道是简单题,属于“送分”范畴,要求拿满分,教学中重点解决表述的规范性问题,力争得满分;中间两道题中等难度题,属于“拉分题”,要求尽力做完,力争每题得分在10分以上,教学中重点解决解题思路的分析和运算的准确性以及速度问题;最后两道题是把关题,难度较大,要求有扎实的基础和较强的分析、解决问题的能力,教学中,我们的策略是在消除学生的畏难心理的同时,学会分层转化的方法,使学生多得分步分,力争每题得5分以上。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com