
题目列表(包括答案和解析)
13.(1)已知二次函数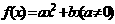 满足条件
满足条件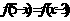 且方程
且方程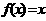 有等根,则
有等根,则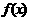 =____;
=____;
(2)已知二次函数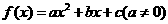 满足条件
满足条件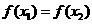 ,则
,则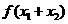 =____;
=____;
(3)己知函数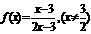 ,若
,若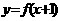 的图像是
的图像是 ,它关于直线
,它关于直线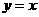 对称图像是
对称图像是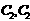 关于原点对称的图像为
关于原点对称的图像为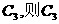 对应的函数解析式是___________;
对应的函数解析式是___________;
(4)若函数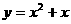 与
与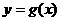 的图象关于点(-2,3)对称,则
的图象关于点(-2,3)对称,则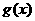 =______
=______
(5)已知函数图象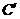 与
与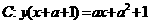 关于直线
关于直线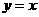 对称,且图象
对称,且图象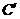 关于点(2,-3)对称,则a的值为______
关于点(2,-3)对称,则a的值为______
(6)已知函数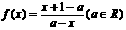 ,函数
,函数 的图像关于点
的图像关于点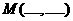 成中心对称图形;
成中心对称图形;
(7) 函数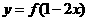 与函数
与函数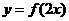 的图像的对称轴是______
的图像的对称轴是______
(8)已知函数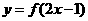 的图象和函数
的图象和函数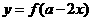 的图象关于直线
的图象关于直线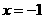 对称,则a=
对称,则a=
(9)若y=f(x)定义域R,则y=f(x-1)与y=f(1-x)图象关于 对称.
(10)在下列给出的四个命题中:①y=f(x+2)与y=f(2-x)的图象关于直线x=2对称 ②若f(x+2)=f(2-x),则f(x)的图象关于直线x=2对称 ③y=f(x-2)与y=f(2-x)的图象关于y轴对称 ④若f(x-2)=f(2-x),则f(x)的图象关于y轴对称。其中正确命题的个数有(B ) A、1个B、2个 C、3个D、4个
(11)设曲线C的方程是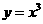 ,曲线C关于点 中心对称,函数
,曲线C关于点 中心对称,函数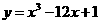 关于点 中心对称。
关于点 中心对称。
(12)函数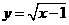 图像关于
图像关于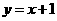 对称的函数是____________
对称的函数是____________
10.(1)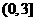 (2)
(2)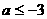 (3)
(3)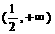 ;(4)(1,2)(5)
;(4)(1,2)(5)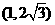 (6)
(6)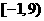 (7)
(7)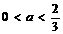 . (8)
. (8)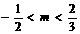 (9)(0,3)。(10)
D(11) A11。(1)
(9)(0,3)。(10)
D(11) A11。(1)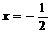 .(2)
.(2)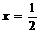 (3)2(4)
A (5)
A (6)B
12.(1)C(2)
(3)2(4)
A (5)
A (6)B
12.(1)C(2)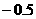 ;(3)
;(3)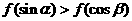 );(4)(B)(5)
);(4)(B)(5)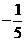
函数基本概念回归课本复习材料4
今天,我怕谁之六
12. 函数的周期性。
(1)类比“三角函数图像”得:
①若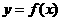 图像有两条对称轴
图像有两条对称轴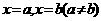 ,则
,则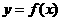 必是周期函数,且一周期为
必是周期函数,且一周期为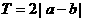 ;
;
②若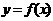 图像有两个对称中心
图像有两个对称中心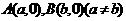 ,则
,则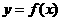 是周期函数,且一周期为
是周期函数,且一周期为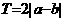 ;
;
③如果函数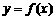 的图像有一个对称中心
的图像有一个对称中心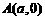 和一条对称轴
和一条对称轴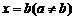 ,则函数
,则函数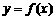 必是周期函数,且一周期为
必是周期函数,且一周期为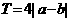 ;
;
(2)由周期函数的定义“函数 满足
满足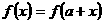
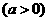 ,则
,则 是周期为
是周期为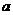 周期函数”得:①函数
周期函数”得:①函数 满足
满足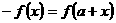 ,则
,则 是周期为2
是周期为2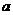 的周期函数;
的周期函数;
②若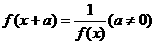 恒成立,则
恒成立,则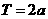 ;
;
③若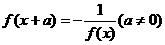 恒成立,则
恒成立,则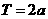 .
.
11. 常见的图象变换
①函数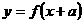
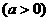 的图象是把函数
的图象是把函数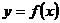 的图象沿
的图象沿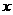 轴向左平移
轴向左平移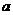 个单位得到的。
个单位得到的。
②函数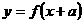 (
(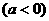 的图象是把函数
的图象是把函数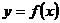 的图象沿
的图象沿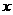 轴向右平移
轴向右平移 个单位得到的。、
个单位得到的。、
③函数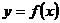 +
+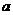
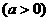 的图象是把函数
的图象是把函数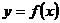 助图象沿
助图象沿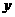 轴向上平移
轴向上平移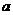 个单位得到的;
个单位得到的;
④函数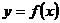 +
+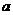
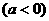 的图象是把函数
的图象是把函数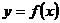 助图象沿
助图象沿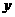 轴向下平移
轴向下平移 个单位得到的;
个单位得到的;
⑤函数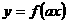
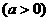 的图象是把函数
的图象是把函数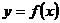 的图象沿
的图象沿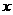 轴伸缩为原来的
轴伸缩为原来的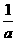 得到的。
得到的。
⑥函数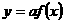
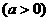 的图象是把函数
的图象是把函数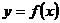 的图象沿
的图象沿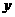 轴伸缩为原来的
轴伸缩为原来的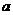 倍得到的.
倍得到的.
10.函数的单调性。
(1)确定函数的单调性或单调区间的常用方法:
①在解答题中常用:定义法(取值――作差――变形――定号)、导数法(在区间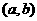 内,若总有
内,若总有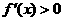 ,则
,则 为增函数;反之,若
为增函数;反之,若 在区间
在区间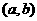 内为增函数,则
内为增函数,则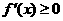 ,请注意两者的区别所在。
,请注意两者的区别所在。
②在选择填空题中还可用数形结合法、特殊值法等等,特别要注意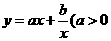
 型函数的图象和单调性在解题中的运用:增区间为
型函数的图象和单调性在解题中的运用:增区间为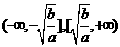 ,减区间为
,减区间为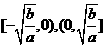 .
.
③复合函数法:复合函数单调性的特点是同增异减,
(2)特别提醒:求单调区间时,一是勿忘定义域;二是在多个单调区间之间不一定能添加符号“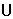 ”和“或”;三是单调区间应该用区间表示,不能用集合或不等式表示.
”和“或”;三是单调区间应该用区间表示,不能用集合或不等式表示.
(3)你注意到函数单调性与奇偶性的逆用了吗?(①比较大小;②解不等式;③求参数范围).
12.(1)若 是定义在R上的奇函数且
是定义在R上的奇函数且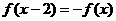 ,给出下列4个结论,不正确的是( )
,给出下列4个结论,不正确的是( )
A. 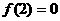 B.
B. 是以4为周期的函数 C.
是以4为周期的函数 C. 的图像关于直线
的图像关于直线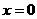 对称 D.
对称 D.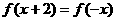
(2) 设 是
是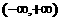 上的奇函数,
上的奇函数,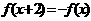 ,当
,当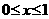 时,
时,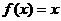 ,则
,则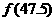 等于____;
等于____;
(3)定义在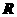 上的偶函数
上的偶函数 满足
满足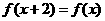 ,且在
,且在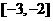 上是减函数,若
上是减函数,若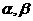 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则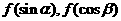 的大小关系为______
___ ;
的大小关系为______
___ ;
(4)已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则,f(6)的值为 ( )
(A)-1 (B) 0 (C) 1 (D)2
(5)函数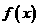 对于任意实数
对于任意实数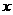 满足条件
满足条件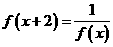 ,若
,若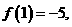 则
则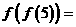 _______
_______
友情提示
11.(1)若函数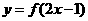 是偶函数,则函数
是偶函数,则函数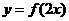 的对称轴方程是______.
的对称轴方程是______.
(2)直线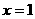 是函数
是函数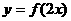 的图象的一条对称轴,那么
的图象的一条对称轴,那么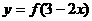 的图象关于
的图象关于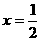 对称
对称
(3)函数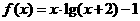 的图象与
的图象与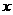 轴的交点个数有____个
轴的交点个数有____个
(4)若0<a<1,b<-1,则函数f(x)=ax+b的图象不经过( )
A.第一象限 B.第二象限C.第三象限 D.第四象限
(5)若0<a<1,则函数y=loga(x+5)的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(6)函数y=a|x|(a>1)的图象是( )

10.(1)已知函数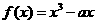 在区间
在区间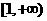 上是增函数,则
上是增函数,则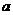 的取值范围是____;
的取值范围是____;
(2)若函数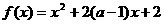 在区间(-∞,4] 上是减函数,那么实数
在区间(-∞,4] 上是减函数,那么实数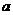 的取值范围是____;
的取值范围是____;
(3)已知函数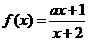 在区间
在区间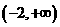 上为增函数,则实数
上为增函数,则实数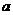 的取值范围_____;
的取值范围_____;
(4)函数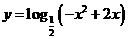 的单调递增区间是________。
的单调递增区间是________。
(5)若函数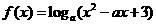 在区间
在区间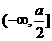 上为减函数,求
上为减函数,求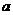 的取值范围
;
的取值范围
;
(6)函数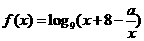 在
在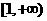 上是增函数,求
上是增函数,求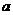 的取值范围
.
的取值范围
.
(7)已知函数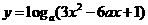 在
在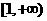 上是减函数,则实数
上是减函数,则实数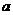 的取值范围是
.
的取值范围是
.
(8)已知奇函数 是定义在
是定义在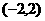 上的减函数,若
上的减函数,若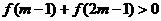 ,求实数
,求实数 的取值范围
的取值范围
(9)函数 在
在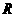 上增函数,图像过
上增函数,图像过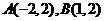 ,则不等式
,则不等式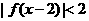 的解集
。
的解集
。
(10)下列函数既是奇函数,又在区间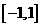 上单调递减的是( )
上单调递减的是( )
(A)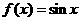 (B)
(B)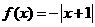 (C)
(C)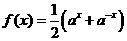 (D)
(D)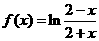
(11)若函数f(x)=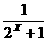 , 则该函数在(-∞,+∞)上是
( )
, 则该函数在(-∞,+∞)上是
( )
(A)单调递减无最小值 (B) 单调递减有最小值 (C)单调递增无最大值 (D) 单调递增有最大值
9.函数的奇偶性。
(1)具有奇偶性的函数的定义域的特征:定义域必须关于原点对称!为此确定函数的奇偶性时,务必先判定函数定义域是否关于原点对称。
(2)确定函数奇偶性的常用方法(若所给函数的解析式较为复杂,应先化简,再判断其奇偶性):
①定义法:②利用函数奇偶性定义的等价形式: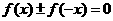 或
或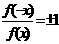 (
(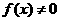 )。③图像法:奇函数的图象关于原点对称;偶函数的图象关于
)。③图像法:奇函数的图象关于原点对称;偶函数的图象关于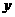 轴对称。
轴对称。
(3)函数奇偶性的性质:
①奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同;偶函数在关于原点对称的区间上若有单调性,则其单调性恰恰相反.
②如果奇函数有反函数,那么其反函数一定还是奇函数.
③若 为偶函数,则
为偶函数,则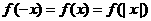 .
.
④奇函数 定义域中含有0,则必有
定义域中含有0,则必有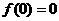 .故
.故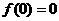 是
是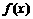 为奇函数的既不充分也不必要条件。
为奇函数的既不充分也不必要条件。
⑤定义在关于原点对称区间上的任意一个函数,都可表示成“一个奇函数与一个偶函数的和(或差)”。
⑥复合函数的奇偶性特点是:“内偶则偶,内奇同外”.⑦既奇又偶函数有无穷多个(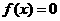 ,定义域是关于原点对称的任意一个数集).6.(1)
,定义域是关于原点对称的任意一个数集).6.(1)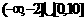 );(2)
);(2)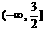 )(3)
)(3)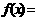
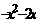 ,
,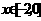 。(4)
。(4)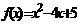 。(5)
。(5)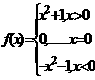 7. (1)
7. (1)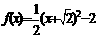 .(2)
.(2)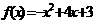 或
或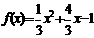 . (3)
. (3)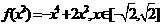 ;(4)
;(4)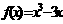 (
( 或
或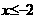 ).(5).
).(5).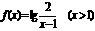 .(6)
.(6)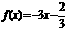 ;(7)
;(7)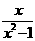 。8. (1)D;(2)
。8. (1)D;(2)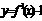 。(3)
。(3)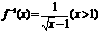 (4):(1,3);(5)
(4):(1,3);(5)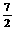 ; (6)1;(7)-2;(8)(1,2)。9.(1)
; (6)1;(7)-2;(8)(1,2)。9.(1) (2)奇。(3)偶(4)
(2)奇。(3)偶(4) )(5) 非奇非偶.(6)偶。(7)奇(8) 1.(9)
)(5) 非奇非偶.(6)偶。(7)奇(8) 1.(9) 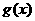 =
=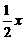
函数基本概念回归课本复习材料3
今天,我怕谁之五
8. 反函数:(1)存在反函数的条件是对于原来函数值域中的任一个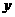 值,都有唯一
值,都有唯一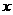 值与之对应,单调函数一定存在反函数,但反之不成立;偶函数只有
值与之对应,单调函数一定存在反函数,但反之不成立;偶函数只有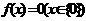 有反函数;周期函数一定不存在反函数。
有反函数;周期函数一定不存在反函数。
(2)求反函数的步骤:①反求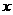 ;②互换
;②互换 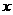 、
、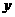 ;③注明反函数的定义域(原来函数的值域)。注意函数
;③注明反函数的定义域(原来函数的值域)。注意函数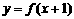 的反函数不是
的反函数不是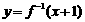 ,而是
,而是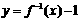 。
。
(3)反函数的性质:①反函数的定义域是原来函数的值域,反函数的值域是原来函数的定义域。②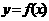 的图象与其反函数
的图象与其反函数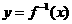 的图象关于直线
的图象关于直线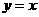 对称,注意函数
对称,注意函数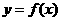 的图象与
的图象与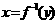 的图象相同。③
的图象相同。③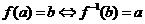 。④互为反函数的两个函数具有相同的单调性和奇函数性。
。④互为反函数的两个函数具有相同的单调性和奇函数性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com