
题目列表(包括答案和解析)
2.向量的数量积的运算律:
(1) a·b= b·a (交换律);
(2)(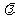 a)·b=
a)·b= 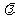 (a·b)=
(a·b)=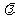 a·b= a·(
a·b= a·(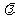 b);
b);
(3)(a+b)·c= a ·c +b·c.
切记:两向量不能相除(相约);向量的“乘法”不满足结合律,
1.实数与向量的积的运算律:设λ、μ为实数,那么(1) 结合律:λ(μa)=(λμ)a;
(2)第一分配律:(λ+μ)a=λa+μa;
(3)第二分配律:λ(a+b)=λa+λb.
(1)理解向量的概念,掌握向量的几何表示,了解共线向量的概念.
(2)掌握向量的加法和减法.
(3)掌握实数与向量的积,理解两个向量共线的充要条件.
(4)了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算.
(5)掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件.
(6)掌握平面两点间的距离公式,以及线段的定比分点和中点坐标公式,并且能熟练运用.掌握平移公式.
[注意]向量是数学的重要概念之一,它给平面解析几何奠定了必要的基础,同时也为物理学提供了工具,这部分内容与实际结合比较密切.在高考中的考查主要集中在两个方面:①向量的基本概念和基本运算;②向量作为工具的应用.
向量.向量的加法与减法.实数与向量的积.平面向量的坐标表示.线段的定比分点.平面向量的数量积.平面两点间的距离.平移.
20.如图,已知三棱锥P-ABC在某个
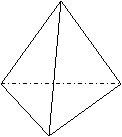 空间直角坐标系中,
空间直角坐标系中,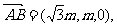 P
P
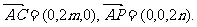
⑴画出这个空间直角坐标系,并指 A C
出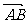 与
与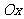 轴的正方向的夹角.
轴的正方向的夹角.
⑵求证: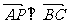 ;
B
;
B
⑶若M为BC的中点,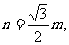
求直线AM与平面PBC所成角的大小.
19.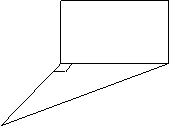 如图,正方形
如图,正方形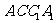 与等腰直角
G
与等腰直角
G
△
|
 ACB互相垂直,∠ACB=
ACB互相垂直,∠ACB=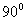 ,E、F
C
A
,E、F
C
A
分别是AB、BC的中点,G是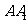 上的点. F E
上的点. F E
⑴如果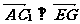 试确定点
试确定点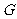 的位置; B
的位置; B
⑵在满足条件⑴的情况下,试求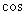 <
<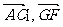 >的值.
>的值.
18.已知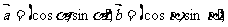 且
且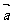 与
与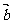 之间满足关系:
之间满足关系: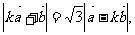 其中k>0.
其中k>0.
⑴用k表示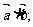
|
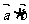 的最小值,并求此时
的最小值,并求此时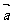 与
与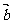 夹角
夹角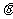 的大小. C
的大小. C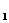 A
A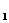
17.在平行四边形ABCD中,A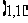 ,
,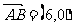 ,点M是线段AB的中点,线段CM与BD交于点P.
,点M是线段AB的中点,线段CM与BD交于点P.
⑴若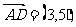 求点C的坐标;
求点C的坐标;
⑵当|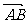 |=|
|=|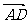 |时,求点P的轨迹.
|时,求点P的轨迹.
16.已知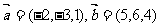 ,则以
,则以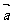 、
、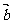 为边的平行四边形的两条高的长 .
为边的平行四边形的两条高的长 .
15.已知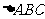 中,
中,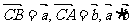 <0,
<0,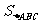 =
=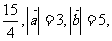
则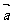 与
与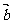 的夹角为 .
的夹角为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com