
题目列表(包括答案和解析)
7.某公司生产一种产品,固定成本为2000元,每生产一单位产品,成本增加100元,已知总收入R
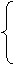 -
-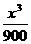 +400x,
0≤x≤390
+400x,
0≤x≤390
与年产量x的关系是R(x)= 则总利润最大时,每年生产的产品单
90090, x>390
位数是( )
A.150 B.200 C.250 D.300
联想:(1)设函数y=f (x)是一次函数,若f (1)=-1,且f′(-2)=-4,则f (x)为( )
A.y=-4x+3 B.y=4x-3 C.y=-4x D.y=-x
(2)如果函数y=x4-8x2+c在[-1,3]上的最小值是-14,那么c=( )
A.1 B.2 C.-1 D.-2
(3)设函数f (x)=x3+ax2+bx+c,且f (0)=0,若f (0)是函数的极值,则( )
A.b≠0 B.当a>0时,f (0)为极大值 C.b=0 D.当a<0时,f (0)为极小值
(4)已知函数f (x)=-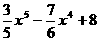 ,则
,则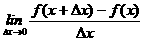 =
。
=
。
(5)设函数f (x)=x3+ax2+bx-1,若当x=1时,有极值为1,则函数g(x)=x3+ax2+bx的单调递减区间为 。
6.等比数列{an}公比为q,则“a1>0,且q>1”是“对于任意自然数n,都有an+1>an”的( )
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件
联想(1)数列满足条件:①任意连续二项的和大于零;②任意连续三项的和小于零;则这样的数列最多有 项。
(2)a、b为不相等的正实数,且a,x,y,b成A·P,a,m,n,b成G·P,则下列关系成立是( )
A.x+y>m+n B.x+y=m+n C.x+y<m+n D.x+y与m+n的大小关系不定
(3)数列{an}是公差不为零的等差数列,并且a5,a8,a13是等比数列{bn}的相邻三项。若b2=5,则b2等于( )
A.5·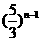 B.5·
B.5·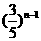 C.3·
C.3·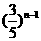 D.3·
D.3·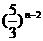
5.若不等式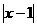 <a成立的充分条件是0<x<4,则a的取值范围是( )
<a成立的充分条件是0<x<4,则a的取值范围是( )
A.a≥1 B.a≥3 C.a≤1 D.a≤3
联想:(1)若关于x的不等式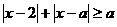 在R上恒成立,则实数a的取值范围是( )
在R上恒成立,则实数a的取值范围是( )
A.a≥1 B.a≤1 C.a≥-1 D.a≤0
(2)f (x)的图象是如图两条线段,它的定义域是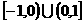 ,
,
则不等式f (x)-f (-x)>-1的解集是 。
(3)若对实数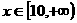 恒有
恒有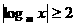 ,则实数m的取值范围是 。
,则实数m的取值范围是 。
4.已知△ABC中,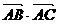 ≤0,sinA+cosA≥1,则∠A为( )
≤0,sinA+cosA≥1,则∠A为( )
A.=90° B.≠90° C.>90° D.<90°
联想:(1)若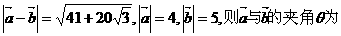 ( )
( )
A.30° B.60° C.120° D.150°
(2)已知点A(2,1),B(1,2),且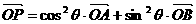 ,则点P(x,y)的轨迹方程是
。
,则点P(x,y)的轨迹方程是
。
(3)已知向量 关于y轴对称,且
关于y轴对称,且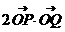 =1,则点P(x,y)的轨迹方程是
。
=1,则点P(x,y)的轨迹方程是
。
(4)在△ABC中,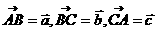 ,且
,且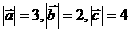 ,则
,则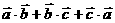 的值为
。
的值为
。
(5)已知向量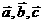 两两所成的角相等,且不共线,
两两所成的角相等,且不共线,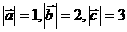 ,则向量
,则向量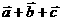 的长度为
,向量
的长度为
,向量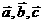 的夹角为
。
的夹角为
。
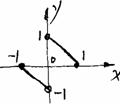 (6)若
(6)若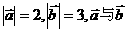 的夹角为120°,则
的夹角为120°,则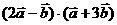 = 。
= 。
3.已知sinα=-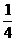 ,α∈
,α∈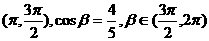 ,则α+β是( )
,则α+β是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
联想:(1)若2sin2α+sin2β-2sinα=0,则cos2α+cos2β的取值范围是( )
A.[1,5]
B.[1,2]
C.[1,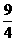 ] D.[-1,2]
] D.[-1,2]
(2)若f (x)=sin(x+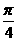 ),x∈
),x∈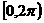 ,且关于x的方程f (x)=m有两个不等实根x1,x2,则x1+x2为( )
,且关于x的方程f (x)=m有两个不等实根x1,x2,则x1+x2为( )
A.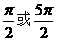 B.
B.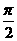 C.
C.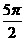 D.不确定
D.不确定
(3)计算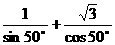 =
。
=
。
(4)已知tanα=2,tan(α-β)=-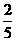 ,那么tanβ= 。
,那么tanβ= 。
2.已知a>0且a≠1,f (x)=x2-ax,当x∈(-1,1)时,均有f (x)<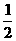 ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.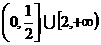 B.
B.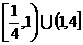 C.
C.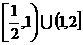 D.
D.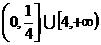
联想:(1)设函数f (x)=x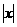 +bx+c,给出四个命题:①c=0时,y=f (x)是奇函数;②b=0,c>0时,方程f (x)=0只有一个实数根;③y=f (x)的图象关于点(o,c)对称;④方程f (x)=0至多有两个实根。上述命题中所有正确的命题的序号是
。
+bx+c,给出四个命题:①c=0时,y=f (x)是奇函数;②b=0,c>0时,方程f (x)=0只有一个实数根;③y=f (x)的图象关于点(o,c)对称;④方程f (x)=0至多有两个实根。上述命题中所有正确的命题的序号是
。
(2)若不等式(关于x)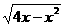 >2ax的解集为(0,2),则实数a的取值范围是
。
>2ax的解集为(0,2),则实数a的取值范围是
。
(3)函数f (x)=logax在x∈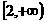 时,
时,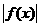 >1恒成立,则实数a的取值范围为( )
>1恒成立,则实数a的取值范围为( )
A.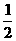 <a<2且a≠1 B.1<a<2 C.0<a<1或1<a<2 D.a>2或0<a<
<a<2且a≠1 B.1<a<2 C.0<a<1或1<a<2 D.a>2或0<a<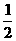
(4)方程sinx+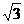 cosx=a在
cosx=a在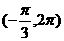 上有两个相异实根α,β,则实数a的取值范围是
,tan(α+β)= 。
上有两个相异实根α,β,则实数a的取值范围是
,tan(α+β)= 。
1.函数f (x)满足f (x+3)=x,若f-1(x)的定义域为[1,4],则f (x)的定义域为( )
A.[1,4] B.[2,8] C.[4,7] D.[3,7]
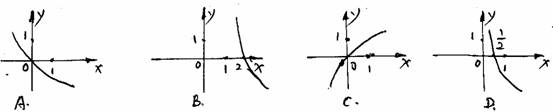 联想:(1)函数f (x)=ax(a>0且a≠1),f-1(2)<0,则f-1(x+1)的图象是( )
联想:(1)函数f (x)=ax(a>0且a≠1),f-1(2)<0,则f-1(x+1)的图象是( )
(2)函数y=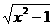 (x≤-1)的反函数是
。
(x≤-1)的反函数是
。
(3)函数f (x)与g (x)的图象关于直线y=x对称,函数h (x)的反函数是g (x-2),若f (3)=7,则h (3)=
。
(4)若函数y=x2-4tx+5在x∈(1,+∞)上存在反函数,则t的取值范围是 。
(5)点(2,2)既在函数f (x)=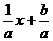 的图象上,又在其反函数的图象上,则适合条件的数组(a,b)有( )
的图象上,又在其反函数的图象上,则适合条件的数组(a,b)有( )
A.1组 B.2组 C.3组 D.无数组
(6)若函数f (x)=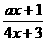 的反函数是f-1(x)=
的反函数是f-1(x)=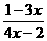 ,则a=( )
,则a=( )
A.1 B.-2 C.2 D.1或-2
例8、如图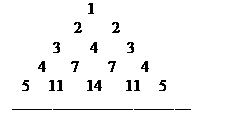 是一个类似“杨辉三角”的图形,第n行共有n个数,且该行的第一个数和最后一个数都是n,中间任意一个数都等于第n-1行与之相邻的两个数的和,
是一个类似“杨辉三角”的图形,第n行共有n个数,且该行的第一个数和最后一个数都是n,中间任意一个数都等于第n-1行与之相邻的两个数的和, 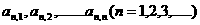 分别表示第n行的第一个数,第二个数,…….第n
个数。
分别表示第n行的第一个数,第二个数,…….第n
个数。
求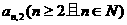 的通项式。
的通项式。
解:(1)由图易知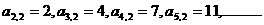 从而知
从而知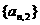 是一阶等差数列,即
是一阶等差数列,即
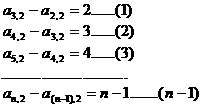
以上n-1个式相加即可得到:
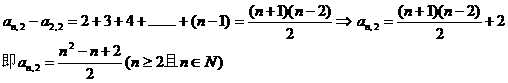
评析:“杨辉三角”型数列创新题是近年高考创新题的热点问题。求解这类题目的关键是仔细观察各行项与行列式的对应关系,通常需转化成一阶(或二阶)等差数列结合求和方法来求解。有兴趣的同学不妨求出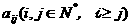 的通项式。
的通项式。
例7、如图,第n个图形由第n+2边形“扩展”而来的。记第n个图形的顶点数为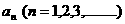 ,则
,则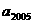 = 。
= 。
解:由图易知: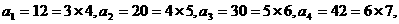 从而易知
从而易知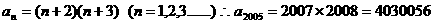
评析:求解几何计数问题通常采用“归纳-猜想-证明”解题思路。本题也可直接求解。第n个图形由第n+2边形“扩展”而来的,这个图形共由n+3个n+2边形组成,而每个n+2边形共有n+2个顶点,故第n个图形的顶点数为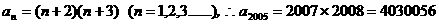 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com