4、圆锥曲线中参数取值范围问题通常从两个途径思考，一是建立函数，用求值域的方法求范围；二是建立不等式，通过解不等式求范围。

3、直线和圆锥曲线位置关系

(1)位置关系判断：△法(△适用对象是二次方程，二次项系数不为0)。

其中直线和曲线只有一个公共点，包括直线和双曲线相切及直线与双曲线渐近线平行两种情形；后一种情形下，消元后关于x或y方程的二次项系数为0。

直线和抛物线只有一个公共点包括直线和抛物线相切及直线与抛物线对称轴平行等两种情况；后一种情形下，消元后关于x或y方程的二次项系数为0。

(2)直线和圆锥曲线相交时，交点坐标就是方程组的解。

　当涉及到弦的中点时，通常有两种处理方法：一是韦达定理；二是点差法。

2、三种圆锥曲线的研究

　 (1)统一定义，三种圆锥曲线均可看成是这样的点集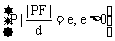：，其中F为定点，d为P到定直线的l距离，F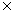l，如图。

因为三者有统一定义，所以，它们的一些性质，研究它们的一些方法都具有规律性。

当0<e<1时，点P轨迹是椭圆；当e>1时，点P轨迹是双曲线；当e=1时，点P轨迹是抛物线。

　 (2)椭圆及双曲线几何定义：椭圆：{P||PF₁|+|PF₂|=2a，2a>|F₁F₂|>0，F₁、F₂为定点}，双曲线{P|||PF₁|-|PF₂||=2a，|F₁F₂|>2a>0，F₁，F₂为定点}。

　 (3)圆锥曲线的几何性质：几何性质是圆锥曲线内在的，固有的性质，不因为位置的改变而改变。

①定性：焦点在与准线垂直的对称轴上

椭圆及双曲线中：中心为两焦点中点，两准线关于中心对称；椭圆及双曲线关于长轴、短轴或实轴、虚轴成轴对称，关于中心成中心对称。

②定量：

	椭　　 圆	双 曲 线	抛 物 线
焦　 距	2c
长轴长	2a	--
实轴长	--	2a
短轴长	2b
焦点到对应 准线距离	P=2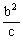	p
通径长	2·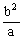	2p
离心率		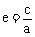1
基本量关系	a2=b2+c2	C2=a2+b2

　 (4)圆锥曲线的标准方程及解析量(随坐标改变而变)

举焦点在x轴上的方程如下：

	椭　　 圆	双 曲 线	抛 物 线
标准方程	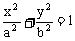(a>b>0)	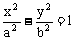(a>0，b>0)	y2=2px(p>0)
顶　 点	(±a，0) (0，±b)	(±a，0)	(0，0)
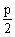焦　 点	(±c，0)	(，0)
准　 线	X=±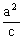	x=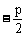
中　 心	(0，0)
有界性	|x|≤a |y|≤b	|x|≥a	x≥0
焦半径	P(x0，y0)为圆锥曲线上一点，F1、F2分别为左、右焦点
|PF1|=a+ex0 　|PF2|=a-ex0	P在右支时： 　|PF1|=a+ex0 　 |PF2|=-a+ex0 P在左支时： 　|PF1|=-a-ex0 　 |PF2|=a-ex0	|PF|=x0+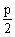

总之研究圆锥曲线，一要重视定义，这是学好圆锥曲线最重要的思想方法，二要数形结合，既熟练掌握方程组理论，又关注图形的几何性质，以简化运算。

1、上一章已经复习过解析几何的基本问题之一：如何求曲线(点的轨迹)方程。它一般分为两类基本题型：一是已知轨迹类型求其方程，常用待定系数法，如求直线及圆的方程就是典型例题；二是未知轨迹类型，此时除了用代入法、交轨法、参数法等求轨迹的方法外，通常设法利用已知轨迹的定义解题，化归为求已知轨迹类型的轨迹方程。因此在求动点轨迹方程的过程中，一是寻找与动点坐标有关的方程(等量关系)，侧重于数的运算，一是寻找与动点有关的几何条件，侧重于形，重视图形几何性质的运用。

在基本轨迹中，除了直线、圆外，还有三种圆锥曲线：椭圆、双曲线、抛物线。

3、求轨迹方程的常规方法。

2、直线和圆锥曲线位置关系。

1、三种圆锥曲线：椭圆、双曲线、抛物线的定义、标准方程、几何性质等。

6．在学习中含有指数、对数的复合函数问题大多数都是以综合形式出现，如与其它函数(特别是二次函数)形成的复合函数问题，与方程、不等式、数列等内容形成的各类综合问题等等，因此要努力提高综合能力。

5．含有参数的指数、对数函数的讨论问题是重点题型，解决这类问题的最基本的分类方案是以“底”大于1或小于1分类；