
题目列表(包括答案和解析)
4、设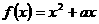 ,
,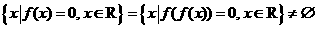 ,
,
则满足条件的所有实数a的取值范围为( )
A.0<a<4 B.a=0 C.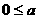 <4 D.0<a
<4 D.0<a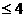
解:
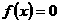 的根为x=0或x=-a
的根为x=0或x=-a
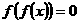 可化为
可化为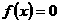 或
或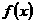 +a=0
+a=0
由题意可得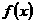 +a=0无解或
+a=0无解或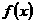 +a=0的根为x=0或x=-a
+a=0的根为x=0或x=-a
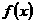 +a=0 即x2+ax+a=0
+a=0 即x2+ax+a=0

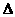 =a2-4a<0或a=0
=a2-4a<0或a=0

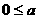 <4。故选C。
<4。故选C。
3、设x,y均为正实数,且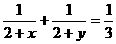 ,则xy的最小值为( )
,则xy的最小值为( )
A.4 B.16 C.8 D.24
解:由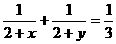 可化为xy =8+x+y
可化为xy =8+x+y
 x,y均为正实数
x,y均为正实数
 xy =8+x+y
xy =8+x+y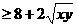 (当且仅当x=y等号成立)
(当且仅当x=y等号成立)
即xy-2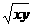 -8
-8
可解得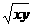

即xy 16故xy的最小值为16。故选B。
16故xy的最小值为16。故选B。
2、若对一切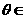 R,向量
R,向量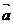 =(a+cos
=(a+cos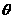 ,2a-sin
,2a-sin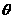 )的长度不超过2,则实数
)的长度不超过2,则实数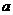 的取值范围为
的取值范围为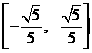 .
.
解:依题意,得 <2
<2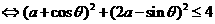
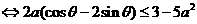
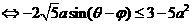 (
(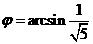 )(对任意实数
)(对任意实数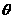 成立)
成立)
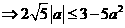
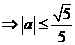 . 故
. 故 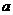 的取值范围为
的取值范围为 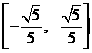 。
。
1、已知动点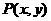 满足x2+y2-
满足x2+y2-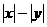 =0,
=0, 为坐标原点,则
为坐标原点,则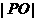 的取值范围是_______
的取值范围是_______
 解:方程x2+y2-
解:方程x2+y2-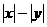 =0可化为:
=0可化为:
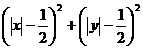 =
=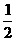
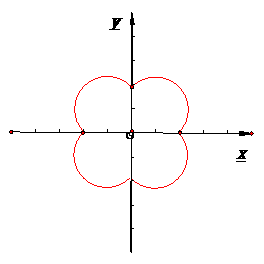
所以动点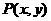 的轨迹如图:为原点和四段圆弧
的轨迹如图:为原点和四段圆弧
故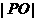 的取值范围是{0}
的取值范围是{0}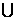
13.两个数列{an}和{bn}满足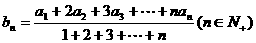
(1)若数列{bn}是等差数列,求证:数列{an}也是等差数列。
(2)试问(1)的逆命题是否成立?若成立,给出证明;若不成立,说明理由。
12.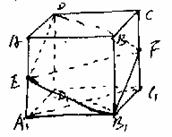 正四棱柱ABCD-A1B1C1D1中,底面边长为
正四棱柱ABCD-A1B1C1D1中,底面边长为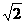 ,侧棱长为
,侧棱长为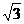 ,E、F分别是AB1、CB1的中点,求证:平面D1EF⊥平面AB1C。
,E、F分别是AB1、CB1的中点,求证:平面D1EF⊥平面AB1C。
联想:直四棱柱ABCD-A1B1C1D1的底面是菱形,AD=AA1=a,∠DAB=600,E,F为AA1,CC1的中点。
(Ⅰ)证明:面B1EF⊥平面BDD1;(Ⅱ)求直四棱
柱被面DEB1F所截得的下半部分的体积;
(Ⅲ)求面DEB1F与底面A1B1C1D1所成的二面角。
11.已知函数f(x)=x4 + (a-2) x2 +(5-a)对任意实数x恒为正值,求实数a的取值范围。
联想:(1)设f ( x) = x2-2ax+2,当x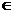
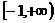 时,f ( x )≥a恒成立,求实数a的取值范围。
时,f ( x )≥a恒成立,求实数a的取值范围。
(2)设函数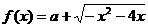 与
与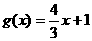 ,若恒有f ( x )≤g ( x )成立,试求实数a的取值范围。
,若恒有f ( x )≤g ( x )成立,试求实数a的取值范围。
(3)已知函数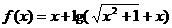 ,若不等式f ( m · 3x ) + f ( 3x-9x-2 ) < 0,对任意
,若不等式f ( m · 3x ) + f ( 3x-9x-2 ) < 0,对任意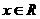 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
10.设圆x2
+ y2 = 4和直线y = x + a相交于A,B两点,这时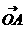 ·
·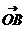 = 其中O是坐标原点,又当两个向量的夹角为300时,a的值为
。
= 其中O是坐标原点,又当两个向量的夹角为300时,a的值为
。
联想:(1)在原点为O的直角坐标平面上,有以点A(4,-3)为直角顶点的Rt△AOB,已知AB的长为OA长的2倍,且点B的纵坐标为正,则
①向量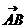 为
。
为
。
②A点关于直线OB的对称点的坐标为 。
(2)已知: = (cosα,sinα),
= (cosα,sinα), 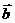 = (cosβ,sinβ),且
= (cosβ,sinβ),且 与
与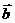 不共线,
不共线,
(Ⅰ)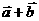 与
与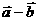 的夹角为
。
的夹角为
。
(Ⅱ)若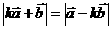 ,且0<α<β<π,k
,且0<α<β<π,k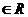 且k ≠0,则β-α的值为 。
且k ≠0,则β-α的值为 。
(3)若将向量 =(2,1)围绕原点按逆时针方向旋转
=(2,1)围绕原点按逆时针方向旋转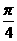 得到向量
得到向量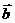 ,则向量
,则向量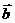 =
=
。
9.已知某企业的总收入函数为R=26x-2x2-4x3,总成本函数C = 8x+x2,其中x表示产品的产量,求企业获得最大利润时的产量为 ,最大利润为 。
联想:用边长为48cm的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒,所做的铁盒容积最大时,在四角截去的正方形的边长为 ( )
A.6 B.8 C.10 D.12
8.数11100-1的末尾连续的零的个数是 ( )
A.0 B.3 C.5 D.7
联想:(1)①2300除以9的余数为 ,②8788+8被88除所得余数为 。
(2)计算某项税率,需用公式y = ( 1- 5x)n(n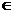 N+)。现已知y的展开式中各项的二项式系数之和为64,用四舍五入的方法计算x =
N+)。现已知y的展开式中各项的二项式系数之和为64,用四舍五入的方法计算x =
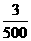 时,y的值,若精确到0.001,其千分位上的数字应是
( )
时,y的值,若精确到0.001,其千分位上的数字应是
( )
A.5 B.4 C.3 D.2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com