
题目列表(包括答案和解析)
6.(搬中)若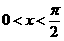 ,求函数
,求函数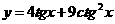 的最大值。
的最大值。
解: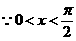
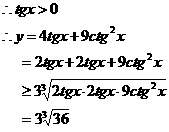
当且仅当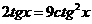
即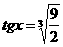 时,等号成立
时,等号成立
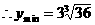
说明:此题容易这样做: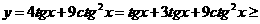
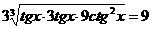 ,但此时等号成立的条件是
,但此时等号成立的条件是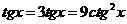 ,这样的
,这样的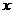 是不存在的。这是忽略了利用不等式求极值时要平均分析的原则。
是不存在的。这是忽略了利用不等式求极值时要平均分析的原则。
5.(搬中)已知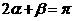 ,求
,求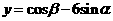 的最小值及最大值。
的最小值及最大值。
解: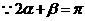
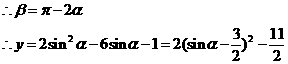
令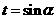
则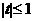
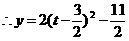
而对称轴为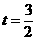
 当
当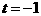 时,
时,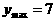 ;
;
当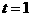 时,
时,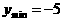
说明:此题易认为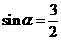 时,
时,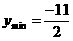 ,最大值不存在,这是忽略了条件
,最大值不存在,这是忽略了条件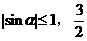 不在正弦函数的值域之内。
不在正弦函数的值域之内。
4.(搬中)求函数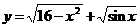 的定义域。
的定义域。
解:由题意有
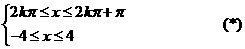
当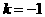 时,
时,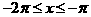 ;
;
当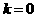 时,
时,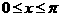 ;
;
当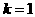 时,
时,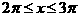
 函数的定义域是
函数的定义域是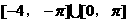
说明:可能会有部分同学认为不等式组(*)两者没有公共部分,所以定义域为空集,原因是没有正确理解弧度与实数的关系,总认为二者格格不入,事实上弧度也是实数。
3.(搬中) 若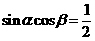 ,求
,求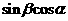 的取值范围。
的取值范围。
解:令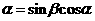 ,则有
,则有
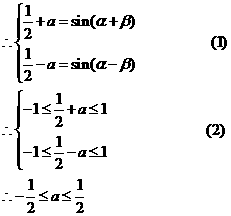
说明:此题极易只用方程组(1)中的一个条件,从而得出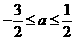 或
或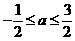 。原因是忽视了正弦函数的有界性。另外不等式组(2)的求解中,容易让两式相减,这样做也是错误的,因为两式中的等号成立的条件不一定相同。这两点应引起我们的重视。
。原因是忽视了正弦函数的有界性。另外不等式组(2)的求解中,容易让两式相减,这样做也是错误的,因为两式中的等号成立的条件不一定相同。这两点应引起我们的重视。
2.(搬中) 求函数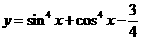 的相位和初相。
的相位和初相。
解: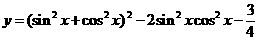
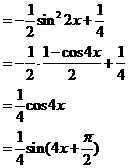
 原函数的相位为
原函数的相位为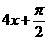 ,初相为
,初相为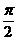
说明:部分同学可能看不懂题目的意思,不知道什么是相位,而无从下手。应将所给函数式变形为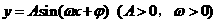 的形式(注意必须是正弦)。
的形式(注意必须是正弦)。
1.(石庄中学)已知定义在区间[-p,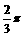 ] 上的函数y=f(x)的图象关于直线x= -
] 上的函数y=f(x)的图象关于直线x= -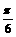 对称,当xÎ[-
对称,当xÎ[-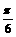 ,
,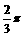 ]时,函数f(x)=Asin(wx+j)(A>0, w>0,-
]时,函数f(x)=Asin(wx+j)(A>0, w>0,-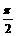 <j<
<j<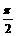 ),其图象如图所示。
),其图象如图所示。
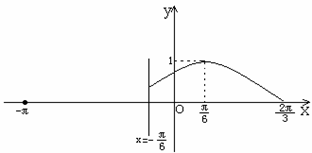 (1)求函数y=f(x)在[-p,
(1)求函数y=f(x)在[-p,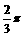 ]的表达式;
]的表达式;
(2)求方程f(x)=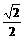 的解。
的解。
解:(1)由图象知A=1,T=4(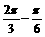 )=2p,w=
)=2p,w=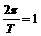
在xÎ[-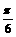 ,
,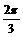 ]时
]时
将(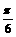 ,1)代入f(x)得
,1)代入f(x)得
f(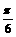 )=sin(
)=sin(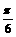 +j)=1
+j)=1
∵-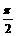 <j<
<j<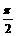
∴j=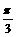
∴在[-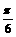 ,
,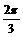 ]时
]时
f(x)=sin(x+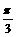 )
)
∴y=f(x)关于直线x=-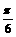 对称
对称
∴在[-p,-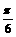 ]时
]时
f(x)=-sinx
综上f(x)=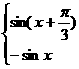
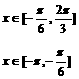
(2)f(x)=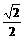
在区间[-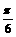 ,
,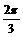 ]内
]内
可得x1=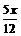 x2=
-
x2=
-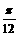
∵y=f(x)关于x= - 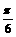 对称
对称
∴x3=-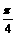 x4= -
x4= -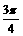
∴f(x)=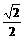 的解为xÎ{-
的解为xÎ{-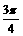 ,-
,-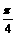 ,-
,-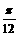 ,
,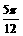 }
}
24.(案中)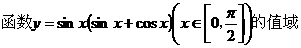 是
。
是
。
正确答案: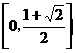
错误原因:如何求三角函数的值域,方向性不明确
23.(案中)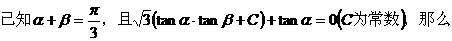
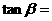 。
。
正确答案: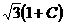
错误原因:两角和的正切公式使用比较呆板。
22.(薛中)函数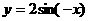 的单调递增区间是
。
的单调递增区间是
。
答案: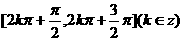
错解: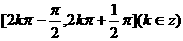
错因:忽视这是一个复合函数。
21.(薛中)关于函数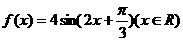 有下列命题,1y=f(x)图象关于直线
有下列命题,1y=f(x)图象关于直线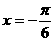 对称 2 y=f(x)的表达式可改写为
对称 2 y=f(x)的表达式可改写为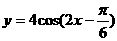 3 y=f(x)的图象关于点
3 y=f(x)的图象关于点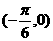 对称 4由
对称 4由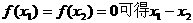 必是
必是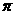 的整数倍。其中正确命题的序号是
。
的整数倍。其中正确命题的序号是
。
答案:23
错解:234
错因:忽视f(x) 的周期是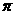 ,相邻两零点的距离为
,相邻两零点的距离为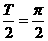 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com