
题目列表(包括答案和解析)
5.将图形F按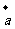 =(h,k)(其中h>0,k>0)平移,就是将图形F( )
=(h,k)(其中h>0,k>0)平移,就是将图形F( )
(A) 向x轴正方向平移h个单位,同时向y轴正方向平移k个单位。
(B) 向x轴负方向平移h个单位,同时向y轴正方向平移k个单位。
(C) 向x轴负方向平移h个单位,同时向y轴负方向平移k个单位。
(D) 向x轴正方向平移h个单位,同时向y轴负方向平移k个单位。
4.设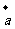 ,
,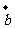 为不共线向量,
为不共线向量,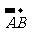 =
=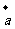 +2
+2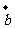 ,
, =-4
=-4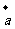 -
-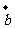 ,
, =
=
-5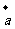 -3
-3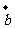 ,则下列关系式中正确的是 ( )
,则下列关系式中正确的是 ( )
(A)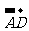 =
=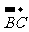 (B)
(B)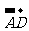 =2
=2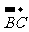
(C)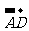 =-
=-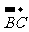 (D)
(D)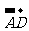 =-2
=-2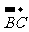
3.已知ABCDEF是正六边形,且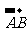 =
=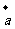 ,
,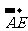 =
=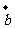 ,则
,则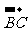 =( )
=( )
(A)
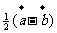 (B)
(B) 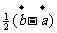 (C)
(C) 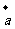 +
+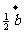 (D)
(D) 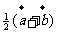
2.已知B是线段AC的中点,则下列各式正确的是( )
(A)
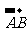 =-
=-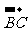 (B)
(B) 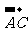 =
=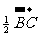 (C)
(C) 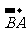 =
=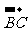 (D)
(D) 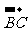 =
=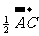
1。已知ABCD为矩形,E是DC的中点,且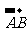 =
=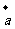 ,
,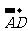 =
=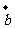 ,则
,则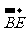 =( )
=( )
(A)
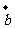 +
+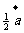 (B)
(B)
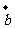 -
-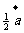 (C)
(C)
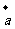 +
+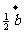 (D)
(D)
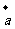 -
-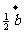
例7.点P在平面上作匀速直线运动,速度是每秒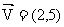 ,当t=0时,P在(-6,-2)处,则t=5时,点P的坐标为________
,当t=0时,P在(-6,-2)处,则t=5时,点P的坐标为________
略解:设所求点P的坐标为(x ,y) 则(x+6 ,y+2)=(10 ,25)
∴x=4 ,y=23 ∴点P的坐标(4 ,23)
例8.已知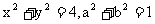 ,试求
,试求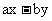 的取值范围。
的取值范围。
解:设有向量p=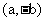 , q
, q , p与q的交角为θ
, p与q的交角为θ
∵p、q都不是零向量(若p=0,则a=b=0,与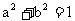 矛盾。同理q≠0)
矛盾。同理q≠0)
∴p•q=ax―by 又p•q=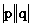 cosθ=
cosθ=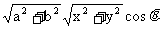 =2 cosθ
=2 cosθ
∴ax―by=2 cosθ ∵-1≤cosθ≤1 ∴-2≤ax―by≤2
高考复习是教师与学生共同创造、共同进步的一个系统工程。随着高考命题的进一步改革,对能力的要求会进一步提高,对教材中新增能力的要求越来越高,在知识交汇点上的命题也不再停留在“戴帽子,穿靴子”的水平上了。因而在复习中应当加强知识点与点之间的渗透与拓宽,构建好知识结构的网络,激活学生的创新思维,增强学生的实践意识与探究能力,真正提高复习的实效,切实提高学生的能力。
教材中利用向量推导出了正弦定理、余弦定理,其实用向量推导其它三角公式也很方便,同时说明向量与三角是有密切联系的。
如: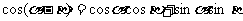
证明:如图:在单位圆上任取两点A、B,设OX为始边,OA、OB为终边的角分别为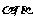
∴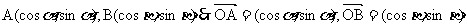
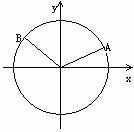 ∴
∴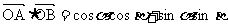
又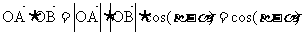
∴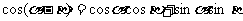
例5.△ABC中,若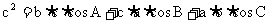
 试判断此三角形的形状。
试判断此三角形的形状。
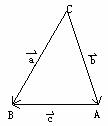
解:设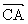 =b ,
=b ,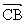 =a ,
=a ,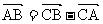 =a-b=c
=a-b=c
∵a与b的夹角为C,b与c的夹角为 ,
,
a与c的夹角为B
∴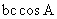 =-
=-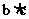 ,
, 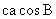 =
=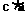 ,
, 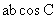 =
=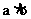
∴ 从而
从而
即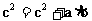 ∴
∴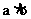 =0 ∴
=0 ∴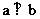
∴△ABC为直角三角形
例6.设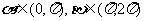 ,向量a=
,向量a=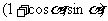 ,b=
,b=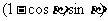
c=(1,0),若a与c的夹角为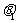 ,b与c的夹角为
,b与c的夹角为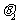 ,且
,且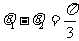 ,
,
求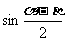 的值
的值
解: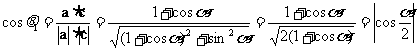
∵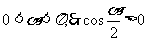 ∴
∴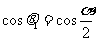
又∵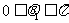 于是
于是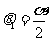
同理可得: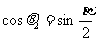 , 因而
, 因而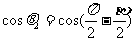
由于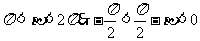 ,而
,而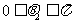 于是
于是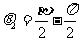
因而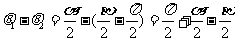
∴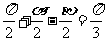 ∴
∴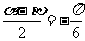 ∴
∴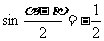
在高中数学里,解析几何的运算等问题是比较繁杂的,而有些问题如果应用向量作形与数的转化,则会大大简化过程。而且向量的坐标是代数与几何联系的纽带,是平面向量的重点内容,它与解析几何联系比较紧密,许多解析几何问题(如长度、角度、点的坐标、轨迹等)都可以用平面向量的知识来解决。
例3. 椭圆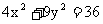 的焦点为
的焦点为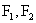 ,点P为其上的动点,当
,点P为其上的动点,当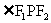 为钝角时,点P横坐标的取值范围是
为钝角时,点P横坐标的取值范围是
解:设点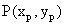 ,则
,则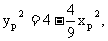
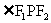 为钝角,则
为钝角,则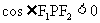 从而
从而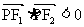
∴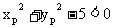 即
即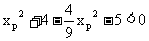
∴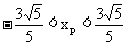
∴点P横坐标的取值范围是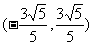
例4.已知椭圆C: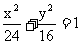 ,直线L:
,直线L: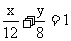 ,P是L上的点,射线OP交C于点
,P是L上的点,射线OP交C于点
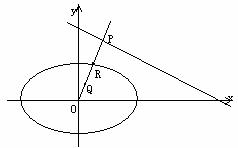 R,又点Q在OP上,且满足
R,又点Q在OP上,且满足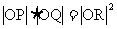 ,当点P在L上移动时,求点Q的方程。(95年全国高考题)
,当点P在L上移动时,求点Q的方程。(95年全国高考题)
解:设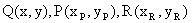
则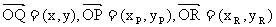
∵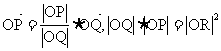
∴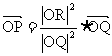
∴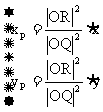 代入L方程得
代入L方程得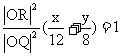
同理可得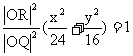 ∴
∴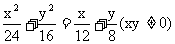
即点Q的轨迹方程为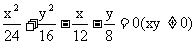
说明:用向量作为工具解决解几问题时,解法简洁明快,而且易理解、易操作。
例1.如图,P是正方形ABCD的对角线BD上一点,PECF是矩形,
证明:①PA=EF ②PA⊥EF
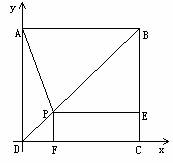 分析:如果用平面几何的常规证法来处理这两个结论,
分析:如果用平面几何的常规证法来处理这两个结论,
由于P点的不确定性,显然对大部分学生来讲很困难,
而如果抓住向量,那么可以把几何关系快速转化为数量
关系,从而通过定量分析得出定性的结果
证明:①以DC所在直线为x轴,以DA所在直线为y轴建
立如图所示的直角坐标系。
设正方形边长为1,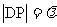 ,
,
则A(0,1),C(1,0),P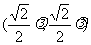 ,E
,E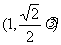 ,F
,F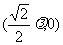
∴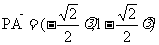
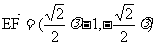
∴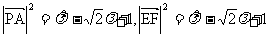 ∴
∴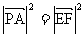 ∴PA=EF
∴PA=EF
②∵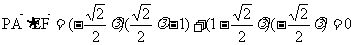
∴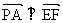 ∴PA⊥EF
∴PA⊥EF
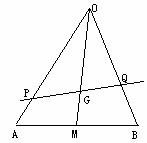
例2.如图,设G是△OAB的重心,过G的直线与OA、OB分别交于P和Q,已知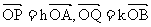 ,△OAB和△OPQ的面积分别为S和T。
,△OAB和△OPQ的面积分别为S和T。
求证:(1)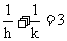 (2)
(2)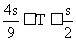
证明:(1)连结OG并延长交AB于M
则M为AB的中点,设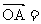 a,
a,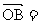 b
b
 ∴
∴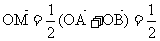 (a+ b)
(a+ b)
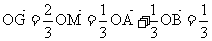 (a+ b)
(a+ b)
又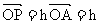 a ,
a ,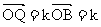 b
b
∴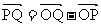 =kb-h a
=kb-h a
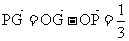 (a+ b)―h a=
(a+ b)―h a=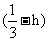 a+
a+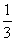 b
b
∵P、G、Q三点共线,∴存在实数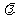 使得
使得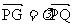
即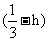 a+
a+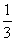 b=
b=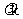 b-
b-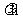 a
a
由平面向量基本定理知: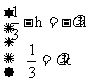 消去
消去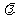 得
得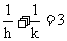
(2)∵∠POQ=∠AOB ∴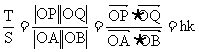
由(1)知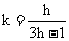 由于
由于
∴ ∴
∴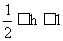
从而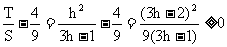 ∴
∴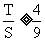
又∵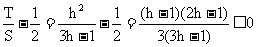 ∴
∴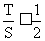
综上所述:∴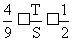 即
即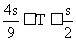
说明:解本题的关键是理解向量的各种运算的定义,并能熟练应用运算法则。利用向量解平面几何问题有时特别方便,但要注意一点,不宜搞得过难过深,因为高考在这方面要求不高,只是在数学竞赛中有较高要求。
25、已知双曲线C的两条渐近线都过原点,且都以点A(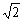 ,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称. (1)求双曲线C的方程.
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称. (1)求双曲线C的方程.
(2)设直线l过点A,斜率为k,当0<k<1时,双曲线C的上支上有且仅有一点B到直线l的距离为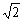 ,试求k的值及此时B点的坐标.
,试求k的值及此时B点的坐标.
解:(1)设双曲线的渐近线为y=kx,由d= =1,解得k=±1.
=1,解得k=±1.
即渐近线为y=±x,又点A关于y=x对称点的坐标为(0,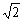 ).
).
∴a=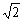 =b,所求双曲线C的方程为x2-y2=2.
=b,所求双曲线C的方程为x2-y2=2.
(2)设直线l:y=k(x-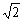 )(0<k<1
)(0<k<1 ,依题意B点在平行的直线l′上,
,依题意B点在平行的直线l′上,
且l与l′间的距离为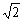 .
.
设直线l′:y=kx+m,应有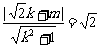 ,化简得m2+2
,化简得m2+2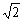 km=2. ②
km=2. ②
把l′代入双曲线方程得(k2-1)x2+2mkx+m2-2=0,
由Δ=4m2k2-4(k2-1)(m2-2)=0.可得m2+2k2=2 ③
②、③两式相减得k=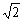 m,代入③得m2=
m,代入③得m2= ,解设m=
,解设m= ,k=
,k=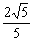 ,此时x=
,此时x= ,y=
,y=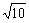 .故B(2
.故B(2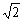 ,
,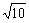 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com