
题目列表(包括答案和解析)
11.(人教版65页第8题)
已知下列等式,比较 ,
,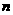 的大小
的大小
(1)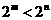 (2)
(2)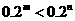
变式1:设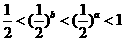 ,那么 ( )
,那么 ( )
A.a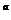 <a
<a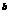 <b
<b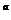 B.a
B.a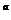 < b
< b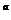 <a
<a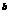
C.a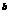 <a
<a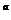 <b
<b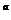 D.a
D.a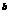 <b
<b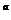 <a
<a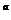
解:由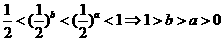 ,在A和B中,
,在A和B中,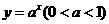 在定义域内是单调递减的,∴
在定义域内是单调递减的,∴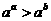 ,所以结论不成立.在C中,
,所以结论不成立.在C中,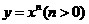 在
在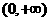 内是单调递增的,又
内是单调递增的,又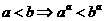 ,所以答案为C.
,所以答案为C.
变式2:已知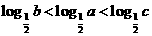 ,则 ( )
,则 ( )
A.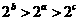 B.
B.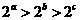
B.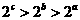 D.
D.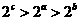
解:由已知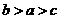 ,因为
,因为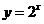 在定义域内是单调递增的,所以
在定义域内是单调递增的,所以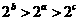
答案为A.
变式3:已知函数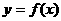 的图象与函数
的图象与函数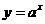 (
(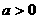 且
且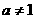 )的图象关于直线
)的图象关于直线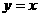 对称,记
对称,记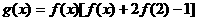 .若
.若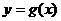 在区间
在区间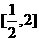 上是增函数,则实数
上是增函数,则实数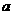 的取值范围是( )
的取值范围是( )
A.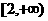 B.
B. C.
C.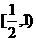 D.
D.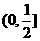
分析:本题根据反函数的定义求出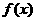 的解析式,再用换元法判断
的解析式,再用换元法判断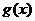 的单调性,结合条件
的单调性,结合条件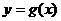 在区间
在区间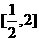 上是增函数,求出实数
上是增函数,求出实数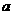 的取值范围是,答案为D
的取值范围是,答案为D
设计意图:考察指、对数函数的单调性
10.(北师大版54页A组第5题)
对于下列函数,试求它们在指定区间上的最大值或最小值,并指出这时的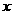 值
值
(2)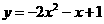 ,
,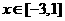
变式1:函数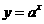 在[0,1]上的最大值与最小值的和为3,则
在[0,1]上的最大值与最小值的和为3,则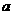 的值为( )
的值为( )
A.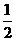 B.2 C.4
D.
B.2 C.4
D.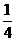
解:当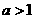 或
或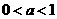 时,函数
时,函数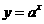 都是定义域上的单调函数,
都是定义域上的单调函数,
∴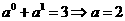 ,故选C.
,故选C.
变式2:若函数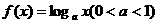 在区间
在区间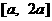 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则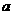 的值为( )
的值为( )
A.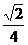 B.
B.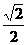 C.
C.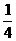 D.
D.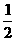
解:∵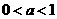 ,∴
,∴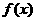 是定义域上的减函数,所以
是定义域上的减函数,所以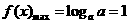 ,
,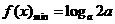 ,∴
,∴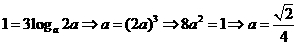 ,故选A
,故选A
设计意图:考察函数的最值
9.(人教版第49页B组第4题)
已知函数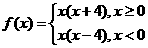 ,求
,求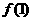 ,
,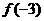 ,
,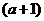 的值
的值
变式1:设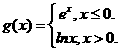 则
则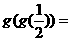 __________
__________
解: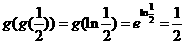 .
.
变式2:已知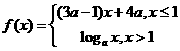 是
是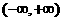 上的减函数,那么
上的减函数,那么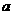 的取值范围是
的取值范围是
A.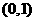 B.
B.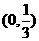
C.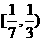 D.
D.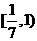
解:分段函数的单调性需分段处理.答案选C
变式3:设函数f(x)=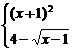
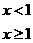 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为
A.(-∞,-2]∪[0,10] B.(-∞,-2]∪[0,1]
C.(-∞,-2]∪[1,10] D.[-2,0]∪[1,10]
解:当x<1时,f(x)≥1 (x+1)2≥1
(x+1)2≥1 x≤-2或x≥0,∴x≤-2或0≤x<1.
x≤-2或x≥0,∴x≤-2或0≤x<1.
当x≥1时,f(x)≥1 4-
4-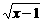 ≥1
≥1
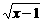 ≤3
≤3 1≤x≤10.
1≤x≤10.
综上,知x≤-2或0≤x≤10.
答案:A
设计意图:考察分段函数的概念和性质
8.(人教版43页B组第3题)
已知函数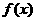 是偶函数,而且在
是偶函数,而且在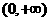 上是减函数,判断
上是减函数,判断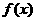 在
在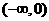 上是增函数还是减函数,并证明你的判断.
上是增函数还是减函数,并证明你的判断.
变式1:下列函数中,在其定义域内既是奇函数又是减函数的是
A. 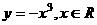 B.
B.
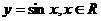
C. 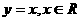 D.
D.
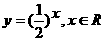
解:B在其定义域内是奇函数但不是减函数;C在其定义域内既是奇函数又是增函数;D在其定义域内不是奇函数,是减函数;故选A.
变式2:函数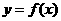 是R上的偶函数,且在
是R上的偶函数,且在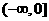 上是增函数,若
上是增函数,若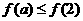 ,则实数
,则实数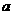 的取值范围是 ( )
的取值范围是 ( )
A.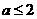 B.
B.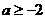 C.
C.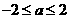 D.
D.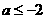 或
或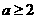
解:当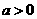 时,∵函数
时,∵函数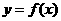 是R上的偶函数,且在
是R上的偶函数,且在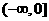 上是增函数,∴
上是增函数,∴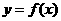 在
在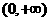 上是减函数,所以若
上是减函数,所以若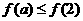 ,则
,则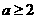 ,当
,当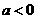 时,函数
时,函数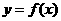 是R上的偶函数,且在
是R上的偶函数,且在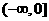 上是增函数,且
上是增函数,且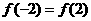 ,∴
,∴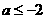 ,故选D
,故选D
设计意图:考察函数奇偶性与单调性的关系
7.(人教A版126页B组第1题)
经济学家在研究供求关系时,一般用纵轴表示产品价格(自变量),而用横轴来表示产品数量(因变量),下列供求曲线,哪条表示厂商希望的供应曲线,哪条表示客户希望的需求曲线?为什么?(图略)
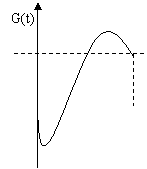
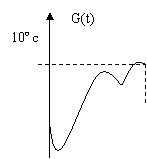
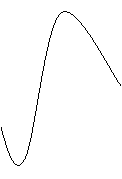
变式1:某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图(1)所示,已知该年的平均气温为10℃,令G(t)表示时间段(0,t)的平均气温,G(t)与t之间的函数关系用下列图象表示,则正确的应该是 ( )
|
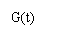
|
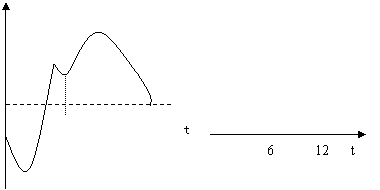

|
|

|
|
|
|
|
|
|||
|
|||
|
|

|
|
|
|
|
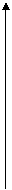

|
|
|
|

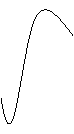
|

|

|
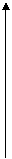


答案:A
变式2:为了稳定市场,确保农民增收,某农产品的市场收购价格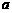 与其前三个月的市场收购价格有关,且使
与其前三个月的市场收购价格有关,且使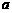 与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
|
月份 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
价格(元/担) |
68 |
78 |
67 |
71 |
72 |
70 |
|
则7月份该产品的市场收购价格应为 ( )
A.69元 B.70元 C.71元 D.72元
答案:C
设计意图:考察学生读图、读表的能力
6.(人教版83页B组第2题)
若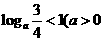 ,且
,且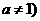 ,求实数
,求实数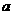 的取值范围.
的取值范围.
变式1:若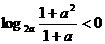 ,则
,则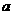 的取值范围是 ( ) A.
的取值范围是 ( ) A.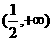 B.
B.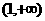 C.
C.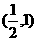 D.
D.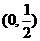
解:当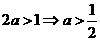 时,若
时,若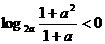 ,则
,则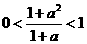
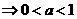 ,∴
,∴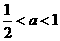
当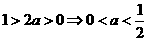 时,若
时,若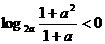 ,则
,则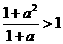
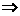
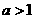 ,此时无解!
,此时无解!
所以选C
变式2:设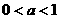 ,函数
,函数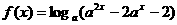 ,则使
,则使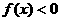 的
的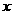 的取值范围是
的取值范围是
(A)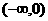 (B)
(B)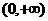 (C)
(C)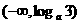 (D)
(D)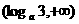
解:要使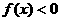 ,且
,且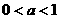 ,所以
,所以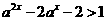
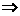
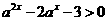
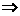
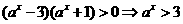 ,又
,又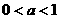 ,∴
,∴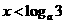 ,故选C.
,故选C.
设计意图:考察对数函数的单调性
5.(人教版第84页B组第4题)
已知函数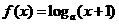 ,
,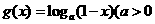 ,且
,且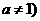
(1) 求函数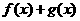 定义域
定义域
(2) 判断函数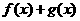 的奇偶性,并说明理由.
的奇偶性,并说明理由.
变式1:已知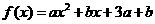 是偶函数,定义域为
是偶函数,定义域为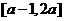 .则
.则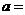 ,
,
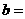
解:函数是偶函数,所以定义域关于原点对称.∴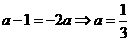 ,
,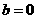
变式2:函数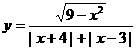 的图象关于
( )
的图象关于
( )
A.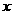 轴对称
B.
轴对称
B.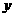 轴对称 C.原点对称 D.直线
轴对称 C.原点对称 D.直线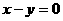 对称
对称
解:函数定义域为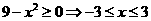 ,所以
,所以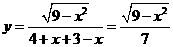 ,所以函数为偶函数,图像关于
,所以函数为偶函数,图像关于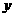 轴对称.
轴对称.
变式3:若函数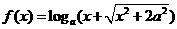 是奇函数,则
是奇函数,则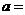
解:由于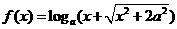 是奇函数,∴
是奇函数,∴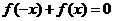 ,
,
即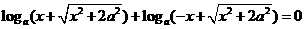 ,
,
∴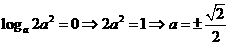 ,又
,又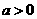 ,∴
,∴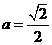
设计意图:考察定义域与奇偶性
4.(北师大版第38页B组第1题)设函数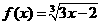 ,
,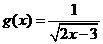 ,求函数
,求函数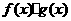 的定义域.
的定义域.
变式1: 函数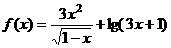 的定义域是
的定义域是
A.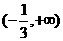 B.
B. 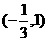 C.
C. 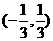 D.
D.
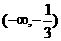
解:由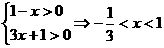 ,故选B.
,故选B.
变式2:设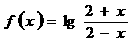 ,则
,则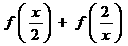 的定义域为
的定义域为
A. 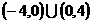 B.
B.
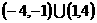
C. 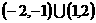 D.
D. 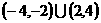
解:选C.由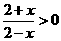 得,
得,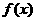 的定义域为
的定义域为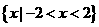 。故
。故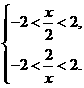 ,解得
,解得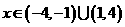 。故
。故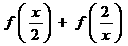 的定义域为
的定义域为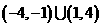
设计意图:考察函数的定义域
3.(北师大版第21页B组第2题)已知集合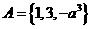 ,
,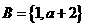 ,是否存在实数
,是否存在实数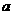 ,使得
,使得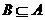 ,若存在,求集合
,若存在,求集合 和
和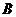 ,若不存在,请说明理由.
,若不存在,请说明理由.
变式1:已知集合A=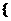 -1,3,2
-1,3,2 -1
-1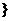 ,集合B=
,集合B=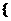 3,
3,
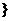 .若
.若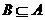 ,则实数
,则实数 = .
= .
解:由已知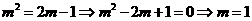
变式2: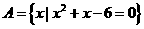 ,
,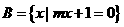 ,且
,且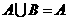 ,则
,则 的取值范围是______ .
的取值范围是______ .
解: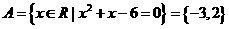 ,当
,当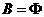 时,
时,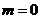 ,当
,当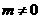 时,
时,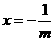 ,所以
,所以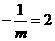 或
或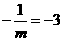 ,所以
,所以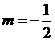 或
或 ,所以
,所以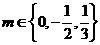
变式3:设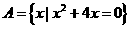 ,
,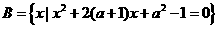 且
且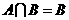 ,求实数
,求实数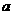 的值.
的值.
解: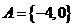 ,因为
,因为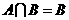 ,所以
,所以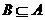 ,所以
,所以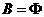 或
或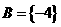 或
或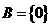 或
或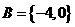 ,当
,当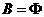 时,
时,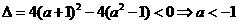 ,当
,当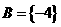 或
或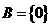 时,
时, 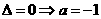 ,
,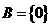 符合题意,当
符合题意,当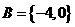 时,
时,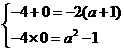
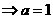
所以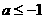 或
或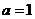
设计意图:结合参数讨论考察集合运算
2.(人教版第14页A组第10题)
已知集合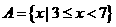 ,
,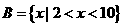 ,求
,求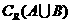 ,
,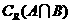 ,
,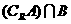 ,
,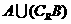
变式1:已知全集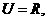 且
且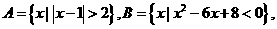 则
则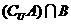 等于 A.
等于 A.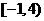 B
B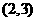 C
C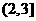 D
D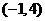
解:答案为C,集合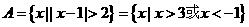 ,
,
所以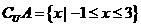 ,集合
,集合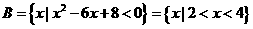 ,
,
所以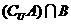 为
为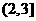
变式2:设集合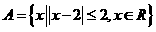 ,
,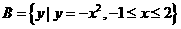 ,则
,则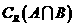 等于( )
等于( )
A.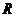 B.
B.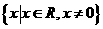 C.
C.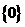 D.
D.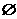
解: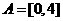 ,
,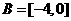 ,所以
,所以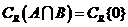 ,故选B。
,故选B。
变式3.已知集合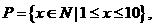 集合
集合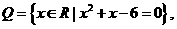 则
则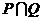 等于
等于
(A)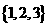 (B)
(B)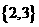 (C)
(C)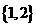 (D)
(D)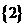
解:集合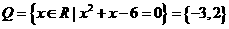 ,所以答案为D.
,所以答案为D.
设计意图:结合不等式考察集合的运算
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com