
题目列表(包括答案和解析)
13.独立事件A,B同时发生的概率
P(A·B)= P(A)·P(B).
12.互斥事件A,B分别发生的概率的和
P(A+B)=P(A)+P(B).
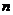 个互斥事件分别发生的概率的和
个互斥事件分别发生的概率的和
P(A1+A2…An)=P(A1)+P(A2)+…+P(An).
11.等可能性事件的概率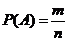 .
.
11.F(x)=(ax+b)n展开式的各项系数和为f(1);
奇数项系数和为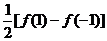 ;
;
偶数项的系数和为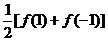 ;
;
10.二项式定理 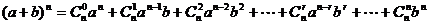 二项展开式的通项公式
二项展开式的通项公式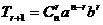
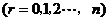 .
.
.二项式系数具有下列性质:
(1) 与首末两端等距离的二项式系数相等;
(2)
若n为偶数,中间一项(第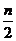 +1项)的二项式系数最大;若n为奇数,中间两项(第
+1项)的二项式系数最大;若n为奇数,中间两项(第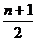 和
和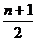 +1项)的二项式系数最大;
+1项)的二项式系数最大;
(3)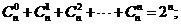
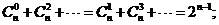
9.分配问题
(1)(平均分组有归属问题)将相异的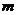 、
、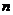 个物件等分给
个物件等分给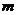 个人,各得
个人,各得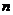 件,其分配方法数共有
件,其分配方法数共有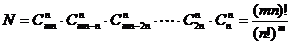 .
.
(2)(平均分组无归属问题)将相异的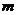 ·
·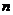 个物体等分为无记号或无顺序的
个物体等分为无记号或无顺序的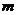 堆,其分配方法数共有
堆,其分配方法数共有
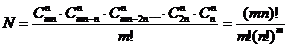 .
.
(3)(非平均分组有归属问题)将相异的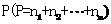 个物体分给
个物体分给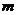 个人,物件必须被分完,分别得到
个人,物件必须被分完,分别得到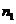 ,
,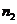 ,…,
,…,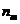 件,且
件,且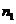 ,
,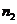 ,…,
,…,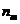 这
这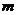 个数彼此不相等,则其分配方法数共有
个数彼此不相等,则其分配方法数共有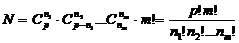 .
.
9.单条件排列
以下各条的大前提是从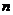 个元素中取
个元素中取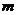 个元素的排列.
个元素的排列.
(1)“在位”与“不在位”
①某(特)元必在某位有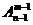 种;
种;
②某(特)元不在某位有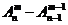 (补集思想)
(补集思想)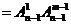 (着眼位置)
(着眼位置)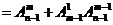 (着眼元素)种.
(着眼元素)种.
(2)紧贴与插空(即相邻与不相邻)
①定位紧贴: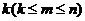 个元在固定位的排列有
个元在固定位的排列有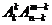 种.
种.
②浮动紧贴: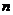 个元素的全排列把k个元排在一起的排法有
个元素的全排列把k个元排在一起的排法有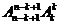 种.注:此类问题常用捆绑法;
种.注:此类问题常用捆绑法;
③插空:两组元素分别有k、h个(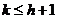 ),把它们合在一起来作全排列,k个的一组互不能挨近的所有排列数有
),把它们合在一起来作全排列,k个的一组互不能挨近的所有排列数有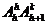 种.
种.
(3)两组元素各相同的插空
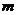 个大球
个大球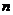 个小球排成一列,小球必分开,问有多少种排法?
个小球排成一列,小球必分开,问有多少种排法?
当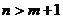 时,无解;当
时,无解;当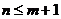 时,有
时,有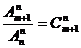 种排法.
种排法.
(4)两组相同元素的排列:两组元素有m个和n个,各组元素分别相同的排列数为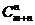 .
.
8.排列数与组合数的关系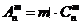 .
.
7.组合恒等式
(1)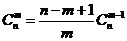 ;
;
(2)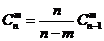 ;
;
(3)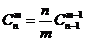 ;
(4)
;
(4)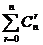 =
=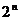 ;
;
(5)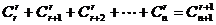 .
.
(6)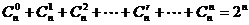 .
.
(7)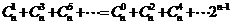 .
.
(8)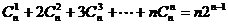 .
.
6.组合数的两个性质
(1)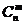 =
=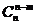 ;(2)
;(2) 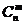 +
+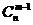 =
=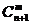 .
.
注:规定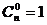 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com