
题目列表(包括答案和解析)
11.解:⑴由已知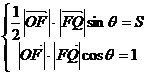 ∴tan
∴tan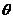 =2S,由
=2S,由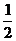 <S<2,得1<tan
<S<2,得1<tan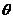 <4.又
<4.又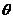 ∈(0,
∈(0,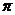 )∴
)∴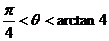 ⑵以O为原点,
⑵以O为原点,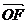 所在直线为X轴建立坐标系,设所求∵S△OFQ=
所在直线为X轴建立坐标系,设所求∵S△OFQ=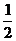 ︱
︱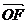 ︱•︱y0︱=
︱•︱y0︱=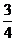 c,∴︱y0︱=
c,∴︱y0︱=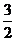 ,∵
,∵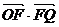 =1,∴(c,0)•(x0-c,y0)=1,解得x0=c+
=1,∴(c,0)•(x0-c,y0)=1,解得x0=c+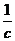 .∴︱
.∴︱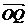 ︱=
︱=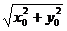 =
=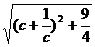 ,注意到当c≥2时,c+
,注意到当c≥2时,c+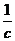 随c的增大而增大,因此当且仅当c=2时,︱
随c的增大而增大,因此当且仅当c=2时,︱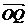 ︱有最小值,此时点Q坐标为(
︱有最小值,此时点Q坐标为( ,-
,-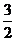 )或(
)或(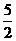 ,
,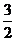 )∴
)∴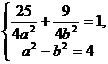 解得
解得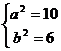 ,故所求椭圆方程为
,故所求椭圆方程为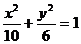
专题4 平面向量(2)答案
10. 解:(1)设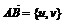 ,则由
,则由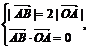 即
即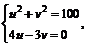 得
得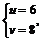 或
或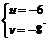
因为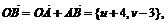 所以 v-3>0,得 v=8,故
所以 v-3>0,得 v=8,故 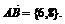
(2)由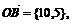 得B(10,5),于是直线OB方程:
得B(10,5),于是直线OB方程: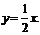 由条件可知圆的标准方程为:(x-3)2+(y+1)2=10,得圆心(3,-1),半径为
由条件可知圆的标准方程为:(x-3)2+(y+1)2=10,得圆心(3,-1),半径为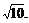 设圆心(3,-1)关于直线OB的对称点为(x,y),则
设圆心(3,-1)关于直线OB的对称点为(x,y),则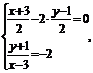 得
得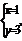 故所求圆的方程为(x-1)2+(y-3)2=10.
故所求圆的方程为(x-1)2+(y-3)2=10.
(3)设P(x1,y1),Q(x2,y2)为抛物线上关于直线OB对称的两点,则
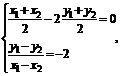 得
得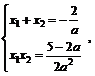 即x1、x2为方程
即x1、x2为方程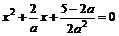 的两个相异实根,
的两个相异实根,
于是由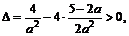 得
得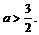 故当
故当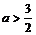 时,抛物线y =ax2-1上总有关于直线OB对称的两点.
时,抛物线y =ax2-1上总有关于直线OB对称的两点.
1.A
2.D 3.D 4.C 5.C 6.A 7.C 8. (5,4) 9.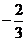
例1.解法一:
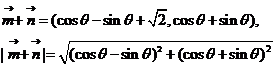
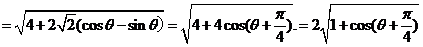
由已知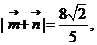 得
得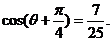 又
又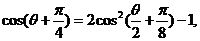
所以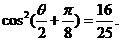
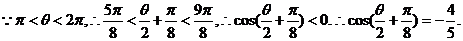
解法二: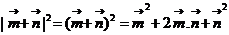
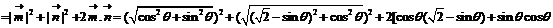
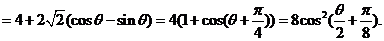 由已知
由已知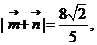
例2.本小题主要考查直线、椭圆及平面向量的基本知识,平面解析几何的基本方法和综合解题能力.
(I)解法一:直线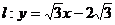 , ① 过原点垂直
, ① 过原点垂直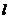 的直线方程为
的直线方程为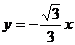 , ②
, ②
解①②得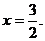 ∵椭圆中心(0,0)关于直线
∵椭圆中心(0,0)关于直线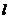 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
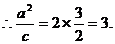 ∵直线
∵直线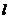 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).
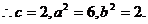 故椭圆C的方程为
故椭圆C的方程为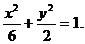 ③
③
解法二:直线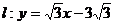 .设原点关于直线
.设原点关于直线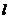 对称点为(p,q),则
对称点为(p,q),则
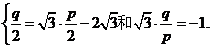 解得p=3.∵椭圆中心(0,0)关于直线
解得p=3.∵椭圆中心(0,0)关于直线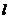 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,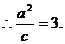 ∵直线
∵直线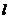 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).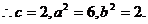 故椭圆C的方程为
故椭圆C的方程为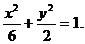 ③
③
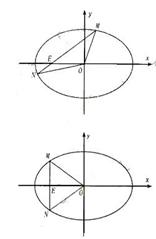
(II)解法一:设M(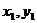 ),N(
),N(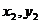 ).当直线m不垂直
).当直线m不垂直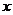 轴时,直线
轴时,直线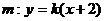 代入③,整理得
代入③,整理得
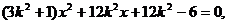
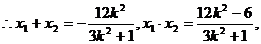
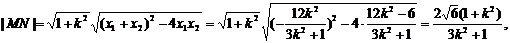
点O到直线MN的距离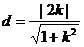
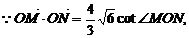
即 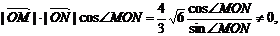
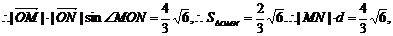 即
即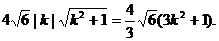 整理得
整理得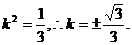 当直线m垂直x轴时,也满足
当直线m垂直x轴时,也满足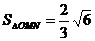 .故直线m的方程为
.故直线m的方程为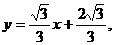 或
或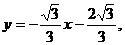 或
或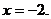
经检验上述直线均满足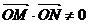 .
.
所以所求直线方程为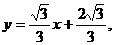 或
或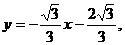
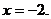
解法二:设M(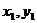 ),N(
),N(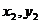 ).
).
当直线m不垂直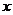 轴时,直线
轴时,直线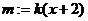 代入③,整理得
代入③,整理得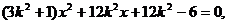
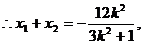 ∵E(-2,0)是椭圆C的左焦点,∴|MN|=|ME|+|NE|
∵E(-2,0)是椭圆C的左焦点,∴|MN|=|ME|+|NE|
=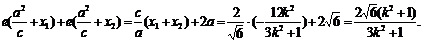 以下与解法一相同.
以下与解法一相同.
解法三:设M(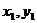 ),N(
),N(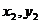 ).设直线
).设直线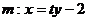 ,代入③,整理得
,代入③,整理得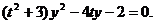
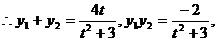
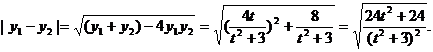
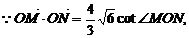 即
即 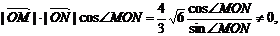
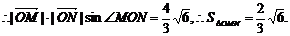
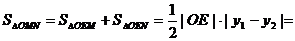
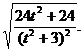 ∴
∴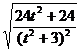 =
=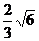 ,整理得
,整理得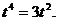 解得
解得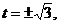 或
或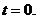 故直线m的方程为
故直线m的方程为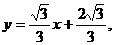 或
或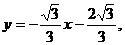 或
或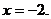 经检验上述直线方程为
经检验上述直线方程为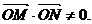
所以所求直线方程为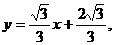 或
或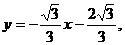 或
或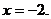
例3.本小题主要考查平面向量的概念和计算,求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程的关系等解析几何的基本思想和综合解题能力,
解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
∵ i=(1,0),c=(0,a),∴ c+li=(l,a),i-2lc=(1,-2la).因此,直线OP和AP的方程为ly=ax 和 y-a=-2lax.消去参数l,得点P(x,y)的坐标满足方程y(y-a)=-2a2x2,
整理得 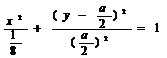 .
①
.
①
因为a>0,所以得:(ⅰ)当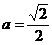 时,方程①是圆方程,故不存在合乎题意的定点E和F;(ⅱ)当
时,方程①是圆方程,故不存在合乎题意的定点E和F;(ⅱ)当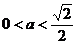 时,方程①表示椭圆,焦点
时,方程①表示椭圆,焦点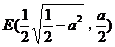 和
和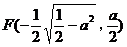 为合乎题意的两个定点:(ⅲ)当
为合乎题意的两个定点:(ⅲ)当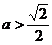 时,方程①也表示椭圆,焦点
时,方程①也表示椭圆,焦点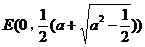 和
和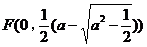 为合乎题意的两个定点.
为合乎题意的两个定点.
11.椭圆的两焦点分别为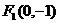 、
、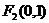 ,直线
,直线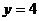 是椭圆的一条准线.
是椭圆的一条准线.
(1)求椭圆的方程;(2)设点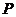 在椭圆上,且
在椭圆上,且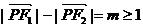 ,求
,求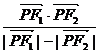 的最大值和最小值.
的最大值和最小值.
专题4 平面向量(1)答案
10.(05湖北)已知向量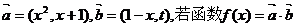 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
8.(04江苏卷)平面向量a,b中,已知a=(4,-3),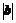 =1,且a·b=5,则向量b=__________.
=1,且a·b=5,则向量b=__________.
9设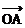 =(3,1),
=(3,1),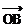 =(-1,2),
=(-1,2),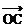 ⊥
⊥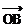 ,
,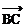 ∥
∥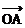 ,试求满足
,试求满足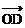 +
+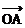 =
=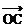 的
的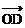 的坐标,其中O为坐标原点。
的坐标,其中O为坐标原点。
7.(02上海)已知向量 和
和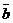 的夹角为120°,且
的夹角为120°,且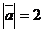 ,
,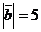 ,则
,则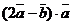 = 。
= 。
6.(04全国4)向量a、b满足(a-b)·(2a+b)=-4,且|a|=2,|b|=4,则a与b夹角的
余弦值等于
5.若向量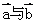 的夹角为
的夹角为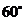 ,
,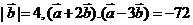 ,则向量
,则向量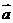 的模为( )
的模为( )
A. 2 B. 4 C. 6 D. 12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com