
题目列表(包括答案和解析)
3.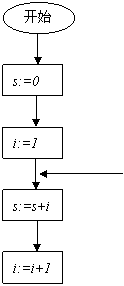 (北师大版第108页练习1 2)
(北师大版第108页练习1 2)
请观察给出的流程图,这是一个求和的算法的流程图,请运行几步看一看,指出该循环结构的循环体,循环变量和循环体的终止条件
|
|



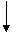

|

解:循环体是 s:=s+i
循环变量是 i
终止条件是 i>4
变式1: 观察给出的流程图,写出输出结果__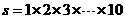 _____
_____
2.(北师大版第100页例3)
设计一个算法,从5个不同的数中找出最大数
变式1:写出“从5个不同数中找出最小数”的一个算法流程
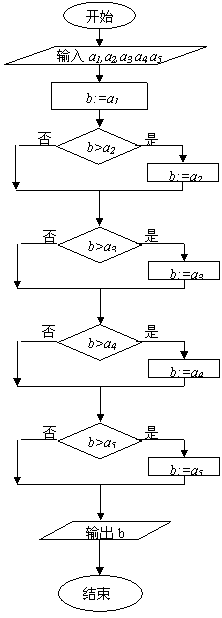 解:
解:
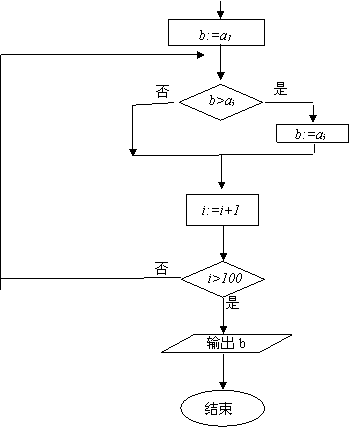
变式2:写出“从100个不同数中找出最小数”的一个算法流程
解:

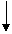
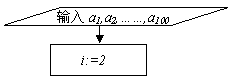
1.(北师大版第92页例6)
求方程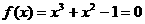 在[0,1]上的近似解,精度为0.01
在[0,1]上的近似解,精度为0.01
变式:用二分法求方程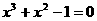 在[0,1]上的近似解,若f(0)=-1,f(0.5)=-0.125,f(1)=1则解可能在区间__[0.5,1]____
在[0,1]上的近似解,若f(0)=-1,f(0.5)=-0.125,f(1)=1则解可能在区间__[0.5,1]____
3.(人教A版选修2-3第36页例2)
(1)求 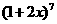 的展开式的第
4 项的系数 ;
的展开式的第
4 项的系数 ;
(2)求 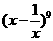 的展开式中
的展开式中 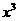 的系数 ?
的系数 ?
变式1:在二项式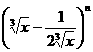 的展开式中,前三项系数的绝对值成等差数列.
的展开式中,前三项系数的绝对值成等差数列.
(1)求展开式的第四项;
(2)求展开式的常数项;
(3)求展开式的各项系数的和.
[分析]:本题旨在训练二项式定理通项公式的运用.
[解答]第一项系数的绝对值为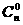 ,第二项系数的绝对值为
,第二项系数的绝对值为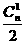 ,第三项系数的绝对值为
,第三项系数的绝对值为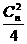 ,
,
依题意有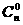 +
+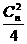 =
=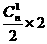 ,解得n=8,
,解得n=8,
(1)第四项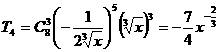 ;
;
(2)通项公式为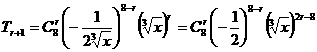 ,展开式的常数项有2r-8=0,即r=4,
,展开式的常数项有2r-8=0,即r=4,
常数项为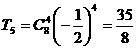 ;
;
(3)令x=1,得展开式的各项系数的和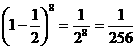 .
.
[点评]本题旨在训练二项式定理通项公式的运用,但要注意通项为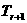 而不是
而不是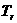 ,这是同学们最容易出错的地方.
,这是同学们最容易出错的地方.
变式2:设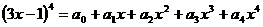 .
.
(1)求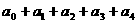 ;
;
(2)求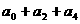 ;
;
(3)求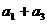 ;
;
(4)求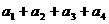 ;
;
(5)求各项二项式系数的和.
[分析]:本题旨在训练二项展开式各项的系数与二项式系数.
[解答](1)令x=1得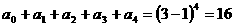 ;
;
(2)令x=-1得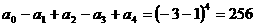 ,
,
而由(1)知: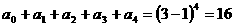 ,
,
两式相加得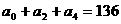 ;
;
(3)将(2)中的两式相减得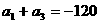 ;
;
(4)令x=0得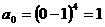 ,得
,得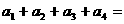
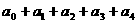 -
-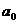 =16-1=15;
=16-1=15;
(5)各项二项式系数的和为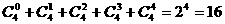 .
.
[点评]①要注意二项展开式各项的系数与二项式系数是不同的两个概念;②系数和与二项式系数和不一定相同,本题的(1)与(5)结果相同纯属巧合;③注意求系数和上述是最一般的方法,一定要理解.
变式3:二项展开式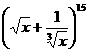 中,有理项的项数是(
)
中,有理项的项数是(
)
|
(A) 3 |
(B) 4 |
(C) 5 |
(D) 6 |
[解析]: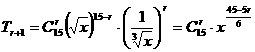 (r = 0,1,2,…,14 ),
(r = 0,1,2,…,14 ),
当r = 3,9,15时,为有理项.
[答案]:A
变式4: 若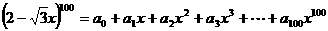 ,
,
求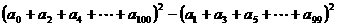 的值.
的值.
[解析]:令x=1得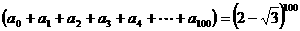 ,
,
令x=-1得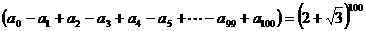
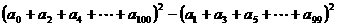
=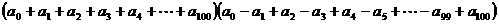
=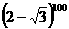
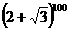
=1
[答案]:1
2.(人教A版选修2-3第29页例4)
在 100 件产品中,有 98 件合格品,2 件次品,从这 100 件产品中任意抽出 3 件。
(1)有多少种不同的抽法 ?
(2)抽出的 3 件中恰好有 1 件是次品的抽法有多少种 ?
(3)抽出的 3 件中至少有 1 件是次品的抽法有多少种 ?
变式1:某人手中有5张扑克牌,其中2张为不同花色的2,3张为不同花色的A,有5次出牌机会,每次只能出一种点数的牌但张数不限,此人有多少种不同的出牌方法?
[分析]:分类讨论,由于情况太多,要做到不重不漏.
[解答]出牌的方法可分为以下几类:
(1)5张牌全部分开出,有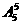 种方法;
种方法;
(2)2张2一起出,3张A一起出,有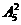 种方法;
种方法;
(3)2张2一起出,3张A分开出,有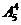 种方法;
种方法;
(4)2张2一起出,3张A分两次出,有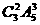 种方法;
种方法;
(5)2张2分开出,3张A一起出,有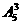 种方法;
种方法;
(6)2张2分开出,3张A分两次出,有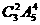 种方法;
种方法;
 因此,共有不同的出牌方法
因此,共有不同的出牌方法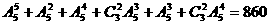 种.
种.
[点评]分类讨论一直是高中的难点,但更是高考的热点内容之一,所以同学们不能回避,应加强训练.
变式2:将7个小球任意放入四个不同的盒子中,每个盒子都不空,
(1)若7个小球相同,共有多少种不同的放法?
(2)若7个小球互不相同,共有多少种不同的放法?
[解析]:(1)解法1:∵7=1+1+1+4=1+1+2+3=1+2+2+2,
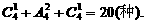 ∴分三类,共有分法
∴分三类,共有分法
解法2(隔板法):将7个小球排成一排,插入3块隔板,
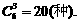 故共有分法
故共有分法
(2)∵7=1+1+1+4=1+1+2+3=1+2+2+2,
∴共有分法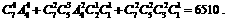
变式3:一个口袋内有4个不同的红球,6个不同的白球,
(1)从中任取4个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7分的
取法有多少种?
[解析]:(1)将取出4个球分成三类情况1)取4个红球,没有白球,有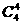 种 2)取3个红球1个白球,有
种 2)取3个红球1个白球,有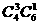 种;3)取2个红球2个白球,有
种;3)取2个红球2个白球,有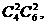

1.(人教A版选修2-3第22页例4)
用 0 到 9 这 10 个数字,可以组成多少个没有重复数字的三位数 ?
变式1: 由1,4,5,x可组成没有重复数字的四位数,若所有这些四位数的各位数字之和为288,则x= .
[解析]:(1+4+5+x)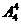 =288,解得10+x=12.
=288,解得10+x=12.
[答案]:x=2.
变式2:在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有 ( )
(A)56个 (B)57个 (C)58个 (D)60个
[解答]解法一:(直接法)
当首位排2,次位排3时,有A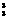 -1种;次位排4、5时有2 A
-1种;次位排4、5时有2 A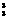 种,共计17种;
种,共计17种;
当首位排3,A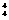 种,共计24种;
种,共计24种;
当首位排4,次位排3时,有A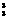 -1种;次位排1、2时有2 A
-1种;次位排1、2时有2 A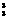 种,共计17种;
种,共计17种;
以上总计17+24+17=58种。
解法二:(间接法)
不作限定时有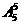 =120种;
=120种;
当首位排1或5时,各有A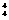 种,共计48种不满足要求;
种,共计48种不满足要求;
当首位排2,次位排1时,有A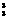 种;而次位排3时有1种,共计7种不满足要求;
种;而次位排3时有1种,共计7种不满足要求;
当首位排4,次位排5时,有A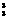 种;而次位排3时有1种,共计7种不满足要求;
种;而次位排3时有1种,共计7种不满足要求;
因此共有120-48-7-7=58种排法,即58个数.
变式3:给定数字0、1、2、3、5、9每个数字最多用一次
(1)可能组成多少个四位数?
(2)可能组成多少个四位奇数?
(3)可能组成多少个四位偶数?
(4)可能组成多少个自然数?
[分析]:注意0不能放在首位,还要注意个位数字,方法多种多样,利用特殊优先法,即特殊的元素,特殊的位置优先考虑.
[解答](1)解法一:从“位置”考虑,由于0不能放在首位,因此首位数字只能有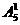 种取法,其余3个数位可以从余下的5个数字(包括0)中任取3个排列,所以可以组成
种取法,其余3个数位可以从余下的5个数字(包括0)中任取3个排列,所以可以组成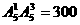 个四位数;
个四位数;
解法二:从“元素”考虑,组成的四位数可以按有无数字0分成两类,有数字0的有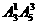 个,无数字0的有
个,无数字0的有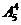 个,所以共组成
个,所以共组成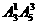 +
+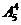 =300个四位数;
=300个四位数;
解法三:“排除法”从6个元素中取4个元素的所有排列中,减去0在首位上的排列数即为所求,所以共有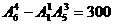 个四位数;
个四位数;
(2)从“位置”考虑,个位数字必须是奇数有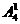 种排法,由于0不能放在首位,因此首位数字只能有
种排法,由于0不能放在首位,因此首位数字只能有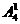 种取法,其余两个数位的排法有
种取法,其余两个数位的排法有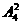 ,所以共有
,所以共有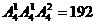 个四位奇数;
个四位奇数;
(3)解法一:由(1)(2)知共有300-192=108个四位偶数;
解法二:从“位置”考虑,按个位数字是否为0分成两种情况,0在个位时,有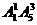 个四位偶数;2在个位时,有
个四位偶数;2在个位时,有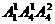 个四位偶数,所以共有
个四位偶数,所以共有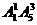 +
+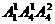 =108个四位偶数;
=108个四位偶数;
(4)一位数:有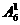 =6个;
=6个;
两位数:有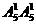 =25个;
=25个;
三位数:有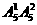 =100个;
=100个;
四位数:有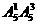 =300个;
=300个;
五位数:有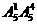 =600个;
=600个;
六位数:有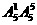 =600个;
=600个;
所以共有6+25+100+300+600+600=1631个自然数.
[点评]解有条件限制的排列问题思路:①正确选择原理;②处理好特殊元素和特殊位置,先让特殊元素占位,或特殊位置选元素;③再考虑其余元素或其余位置;④数字的排列问题,0不能排在首位.
16.(人教版84页B组第5题)
试着举几个满足“对定义域内任意实数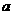 ,
,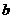 ,都有
,都有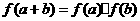 ”的函数例子.
”的函数例子.
变式1:设函数f(x)的定义域是N*,且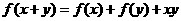 ,
,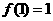 ,则f(25)= ___________________.
,则f(25)= ___________________.
解析:由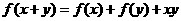
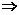
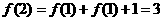
∴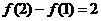
同理,f(3)-f(2)=3.
……
f(25)-f(24)=25.
∴f(25)=1+2+3+…+25=325.
答案:325
变式2:设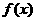 是定义在R上的偶函数,其图象关于直线
是定义在R上的偶函数,其图象关于直线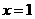 对称,对任意
对称,对任意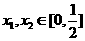 ,都有
,都有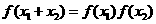
(1)设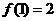 ,求
,求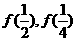
(2)证明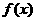 是周期函数.
是周期函数.
(1)解:由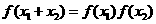 知
知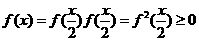 , x∈[0,1].
, x∈[0,1].
因为f(1)=f(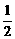 )·f(
)·f(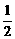 )=[f(
)=[f(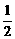 )]2,及f(1)=2,所以f(
)]2,及f(1)=2,所以f(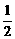 )=2
)=2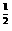 .
.
因为f(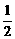 )=f(
)=f(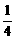 )·f(
)·f(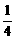 )=[f(
)=[f(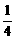 )]2,及f(
)]2,及f(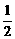 )=2
)=2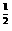 ,所以f(
,所以f(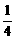 )=2
)=2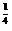 .
.
(2)证明:依题设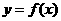 关于直线x=1对称,故f(x)=f(1+1-x)
关于直线x=1对称,故f(x)=f(1+1-x) f(x)=f(2-x),x∈R.
f(x)=f(2-x),x∈R.
又由f(x)是偶函数知f(-x)=f(x),x∈R,所以f(-x)=f(2-x),x∈R.将上式中-x以x代换,得f(x)=f(x+2),x∈R.
这表明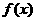 是R上的周期函数,且2是它的一个周期.
是R上的周期函数,且2是它的一个周期.
变式3:设函数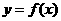 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有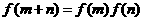 且当
且当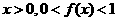
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减;
(3)设集合A={(x,y)|f(x2)·f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,
a∈R},若A∩B=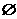 ,求a的取值范围.
,求a的取值范围.
(1)证明:在f(m+n)=f(m)f(n)中,
令m=1,n=0,得f(1)=f(1)f(0).
∵0<f(1)<1,∴f(0)=1.
设x<0,则-x>0.令m=x,n=-x,代入条件式有f(0)=f(x)·f(-x),而f(0)=1,
∴f(x)=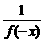 >1.
>1.
(2)证明:设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1.
令m=x1,m+n=x2,则n=x2-x1,代入条件式,得f(x2)=f(x1)·f(x2-x1),
即0<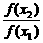 <1.∴f(x2)<f(x1).
<1.∴f(x2)<f(x1).
∴f(x)在R上单调递减.
(3)
解:由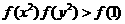
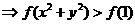
又由(2)知f(x)为R上的减函数,∴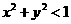
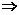 点集A表示圆
点集A表示圆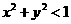 的内部.由f(ax-y+2)=1得ax-y+2=0
的内部.由f(ax-y+2)=1得ax-y+2=0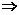 点集B表示直线ax-y+2=0.
点集B表示直线ax-y+2=0.
∵A∩B=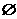 ,∴直线ax-y+2=0与圆
,∴直线ax-y+2=0与圆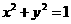 相离或相切。
相离或相切。
于是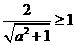
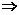
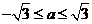
设计意图:考察抽象函数的性质及抽象运算的能力和数形结合的思想。
15.(北师大版第66页B组第3题)
求二次函数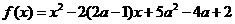 在区间[0,1]上的最小值
在区间[0,1]上的最小值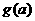 的表达式.
的表达式.
变式1:设a为实数,记函数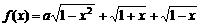 的最大值为g(a).
的最大值为g(a).
(Ⅰ)设t=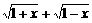 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足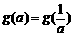 的所有实数a
的所有实数a
解:(I)∵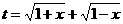 ,
,
∴要使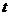 有意义,必须
有意义,必须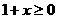 且
且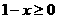 ,即
,即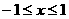
∵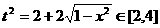 ,且
,且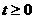 ……① ∴
……① ∴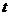 的取值范围是
的取值范围是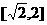 。
。
由①得: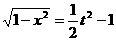 ,∴
,∴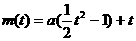
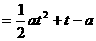 ,
,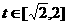 。
。
(II)由题意知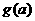 即为函数
即为函数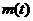
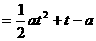 ,
,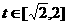 的最大值,
的最大值,
∵直线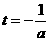 是抛物线
是抛物线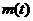
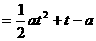 的对称轴,∴可分以下几种情况进行讨论:
的对称轴,∴可分以下几种情况进行讨论:
(1)当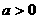 时,函数
时,函数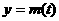 ,
,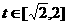 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由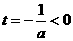 知
知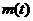 在
在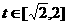 上单调递增,故
上单调递增,故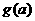
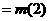
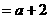 ;
;
(2)当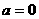 时,
时,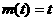 ,
,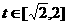 ,有
,有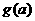 =2;
=2;
(3)当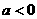 时,,函数
时,,函数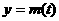 ,
,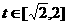 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若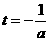
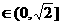 即
即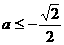 时,
时,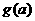
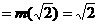 ,
,
若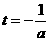
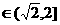 即
即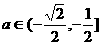 时,
时,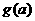
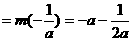 ,
,
若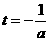
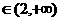 即
即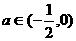 时,
时,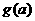
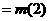
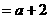 。
。
综上所述,有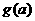 =
=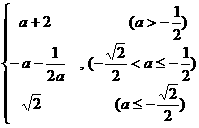 。
。
(III)当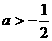 时,
时,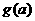
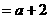
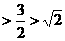 ;
;
当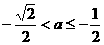 时,
时,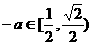 ,
,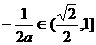 ,∴
,∴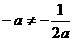 ,
,
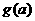
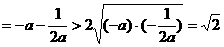 ,故当
,故当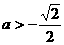 时,
时,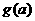
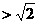 ;
;
当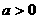 时,
时,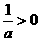 ,由
,由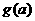
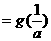 知:
知: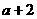
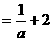 ,故
,故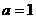 ;
;
当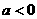 时,
时,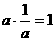 ,故
,故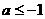 或
或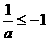 ,从而有
,从而有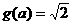 或
或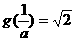 ,
,
要使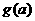
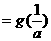 ,必须有
,必须有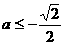 ,
,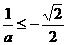 ,即
,即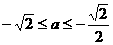 ,
,
此时,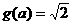
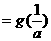 。
。
综上所述,满足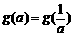 的所有实数a为:
的所有实数a为: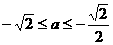 或
或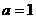 。
。
设计意图:考察二次函数的最值与分类讨论的思想
13.(人教版第49页B组第5题)
证明:
(1)若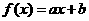 ,则
,则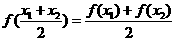
(2)若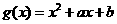 ,则
,则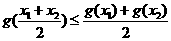
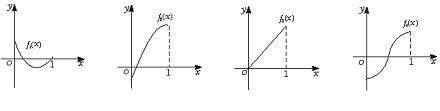
变式1:如图所示,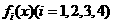 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的
是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的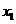 和
和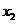 ,任意
,任意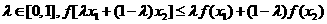 恒成立”的只有 ( )
恒成立”的只有 ( )
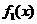
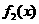
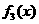
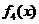
A.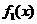 和
和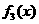 B.
B.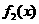 C.
C.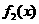 和
和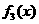 D.
D.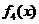
解:当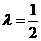 时,符合条件的函数是凹函数,从图像可看出有
时,符合条件的函数是凹函数,从图像可看出有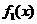 和
和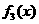 ,选择A.
,选择A.
变式2:.设函数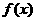 =
=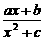 的图象如下图所示,则a、b、c的大小关系是
的图象如下图所示,则a、b、c的大小关系是
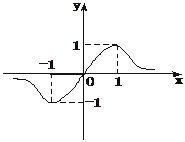
A.a>b>c B.a>c>b C.b>a>c D.c>a>b
解析:f(0)=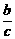 =0,∴b=0.f(1)=1,∴
=0,∴b=0.f(1)=1,∴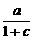 =1.
=1.
∴a=c+1.由图象看出x>0时,f(x)>0,即x>0时,有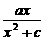 >0,
>0,
∴a>0.又f(x)= 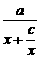 ,
,
当x>0时,要使f(x)在x=1时取最大值1,需x+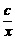 ≥2
≥2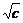 ,
,
当且仅当x=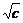 =1时.∴c=1,此时应有f(x)=
=1时.∴c=1,此时应有f(x)=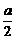 =1.∴a=2.
=1.∴a=2.
答案:B
变式3:如图所示,单位圆中弧AB的长为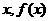 表示弧AB与弦AB
表示弧AB与弦AB
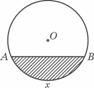 所围成的弓形面积的2倍,则函数
所围成的弓形面积的2倍,则函数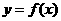 的图象是
的图象是
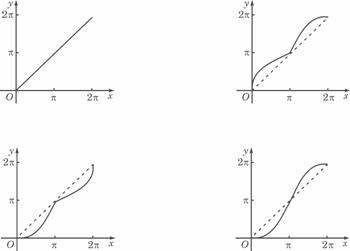
答案:( D )
设计意图:考察图象与式子运算的能力
14:(北师大版136页B组第1题)
判断下列方程在(0,10)内是否存在实数解,并说明理由.
(1)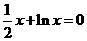 (2)
(2)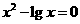
变式1:设二次函数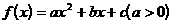 ,方程
,方程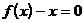 的两个根
的两个根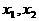 满足
满足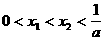 . 当
. 当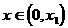 时,证明
时,证明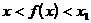 .
.
分析:在已知方程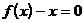 两根的情况下,根据函数与方程根的关系,可以写出函数
两根的情况下,根据函数与方程根的关系,可以写出函数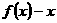 的表达式,从而得到函数
的表达式,从而得到函数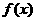 的表达式.
的表达式.
证明:由题意可知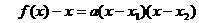 .
.
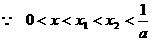 ,
,
∴ 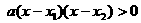 ,
,
∴
当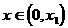 时,
时,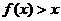 .
.
又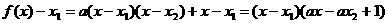 ,
,
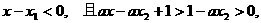
∴
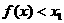 ,
,
综上可知,所给问题获证.
变式2:已知二次函数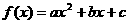 .
.
(1)若a>b>c, 且f(1)=0,证明f(x)的图象与x轴有2个交点;
(2)在(1)的条件下,是否存在m∈R,使得f(m)=- a成立时,f(m+3)为正数,若存在,证明你的结论,若不存在,说明理由;
(3)若对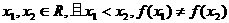 ,方程
,方程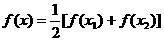 有2个不等实根,
有2个不等实根,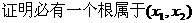
解: (1)
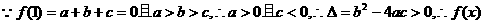
的图象与x轴有两个交点.
(2)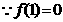 ,∴1是
,∴1是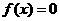 的一个根,由韦达定理知另一根为
的一个根,由韦达定理知另一根为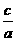 ,
,
∴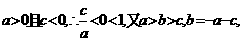
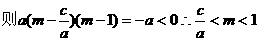
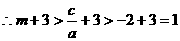
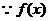 在(1,+∞)单调递增,
在(1,+∞)单调递增,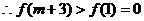 ,即存在这样的m使
,即存在这样的m使
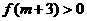
(3)令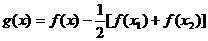 ,则
,则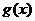 是二次函数.
是二次函数.
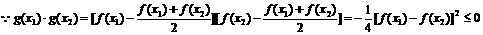
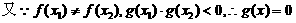 有两个不等实根,且方程
有两个不等实根,且方程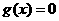 的根必有一个属于
的根必有一个属于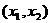 .
.
设计意图:考察函数的零点
12.(人教版48页A组第8题)
设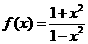 ,求证:(1)
,求证:(1)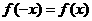 (2)
(2)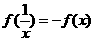
变式1:函数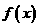 对于任意实数
对于任意实数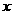 满足条件
满足条件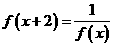 ,若
,若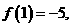 则
则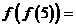 __________.
__________.
解: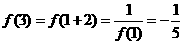 ,
,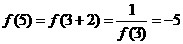 ,又
,又
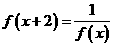 ,∴
,∴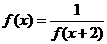 ,
,
∴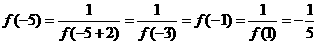
变式2:若奇函数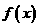
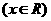 满足
满足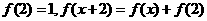 ,则
,则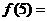
解:由已知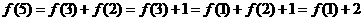 ,令
,令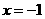 ,则
,则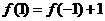 ,又∵
,又∵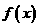 是奇函数,所以
是奇函数,所以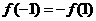 ,
,
∴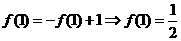 ,∴
,∴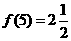
变式3:函数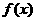 是一个偶函数,
是一个偶函数,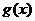 是一个奇函数,且
是一个奇函数,且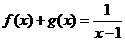 ,则
,则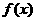 等于
等于
A.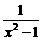 B.
B.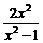 C.
C.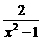 D.
D.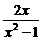
解析:由题知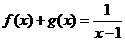 ①
①
以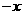 代
代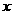 ,①式得
,①式得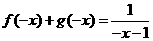 ,即
,即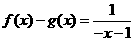 ②
②
①+②得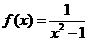
答案:A
设计意图:考察函数的抽象运算与综合性质
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com