
题目列表(包括答案和解析)
5.设A,B,C是△ABC的三个内角,且tanA, tanB是方程6x2-5x+1=0的两个实数根,那么,△ABC是( )
A.钝角三角形 B.锐角三角形 C.等腰三角形 D.等边三角形
联想:(1)△ABC中,tanA=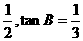 , 边C=1,则最短边长为
。
, 边C=1,则最短边长为
。
(2)△ABC中,tanA=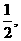 tanB=-2,△ABC的面积为1,则三边长为a=____________, b=___________,
c=__________________
tanB=-2,△ABC的面积为1,则三边长为a=____________, b=___________,
c=__________________
(3)△ABC中,三内角A,B,C的所对的边分别为a,b,c,已知B是A与C的等差中项,a+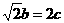 ,则sin C=_________________.
,则sin C=_________________.
(4) 在锐角△ABC中,a,b,c,分别为角A,B,C的对边,A<B<C,B=60°,而且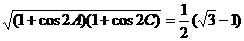 ,求①A,B,C,的大小;②
,求①A,B,C,的大小;② 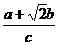 的值。
的值。
(5)已知:sin 2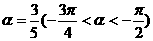 ,函数f(x)=sin(
,函数f(x)=sin(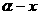 )-sin(
)-sin(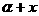 )+2cos
)+2cos .①求cos
.①求cos 的值;②若f-1(x)表示f (x) 在[
的值;②若f-1(x)表示f (x) 在[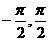 ]上的反函数,试求f-1(
]上的反函数,试求f-1(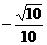 )的值。
)的值。
4.已知函数f(x)=2x-1,g(x)=1-x2,构造函数F(x),定义如下:
当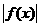 ≥g(x)时,F(x)=
≥g(x)时,F(x)=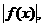 当
当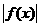 <g(x)时F(x)=-g(x),那么F(x) ( )
<g(x)时F(x)=-g(x),那么F(x) ( )
A.有最小值0,无最大值 B.有最小值-1,无最大值
C.无最小值,有最大值1 D.无最小值,也无最大值
联想:(1)设函数f(x)=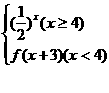 ,则f(log23)=( )
,则f(log23)=( )
A.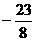 B.
B.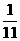 C.
C.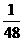 D.
D.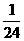
(2)若函数f(x)具有性质:①f(x)为偶函数; ②对任意x∈R,都有f(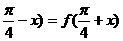 ,则函数f(x)的解析式可以是
.(只须写出满足条件的f(x)的一个解析式即可)
,则函数f(x)的解析式可以是
.(只须写出满足条件的f(x)的一个解析式即可)
(3)设函数f(x)=x2-x+a (a>0),若f(m)<0,则f(m-1)与0的大小关系是 。
3.若函数y=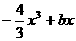 有三个单调区间,则b的取值范围是(
)
有三个单调区间,则b的取值范围是(
)
A.b>0 B.b≥0 C.b<0 D.b≤0
联想:(1)曲线y=2x4上的点到直线y=-x-1的距离的最小值为( )
A.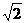 B.
B.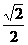 C.
C. 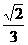 D.
D.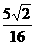
(2)函数y=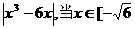 ,
,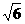 ]时,y的最大值为( )
]时,y的最大值为( )
A.4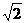 B.3
B.3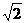 C.2
C.2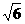 D.
D.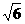
(3)已知函数f(x)=x4-4x3+10x2-27,则方程f(x)=0在[2,10]上的根为( )
A.有3个 B.有2个 C.有且只有一个 D.不存在
(4)设函数f(x)=x3-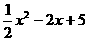 ,若对任意x
,若对任意x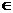 [-1,2], 都有f
(x)<m,则实数m的取值范围为
。
[-1,2], 都有f
(x)<m,则实数m的取值范围为
。
2.若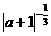 <
<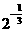 ,则a的取值范围是( )
,则a的取值范围是( )
A.(-3,1) B.(-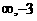 )∪ (1,+
)∪ (1,+ ) C.(
) C.(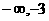 ) D.(
) D.(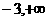 )
)
联想:(1)设f(x)=2x, g(x)=4x, 且g[g(x)]>g[f(x)]>f[g(x)],则x的取值范围是( )
A.(1+∞) B.(-∞,1) C.(0,1) D.(-∞,0)
(2)
不等式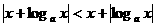 的解集为( )(其中a>0且a≠1)
的解集为( )(其中a>0且a≠1)
(3)设a>0, a≠1,解关于x的不等式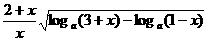 <0
<0
1.设x为直线的倾斜角,且cosx=a,-1<a<o,则x的值为( )
A. B.arccos a C. -arccos a D.
B.arccos a C. -arccos a D. 
联想:(1)直线y=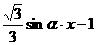 的倾斜角的变化范围是
。
的倾斜角的变化范围是
。
(2)一个直角三角形三内角的正弦值成等比数列,其最小内角是( )
A.arccos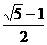 B.arcsin
B.arcsin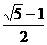 C.arccos
C.arccos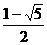 D.arcsin
D.arcsin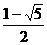
(3) 已知直线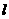 的参数方程为
的参数方程为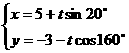 (t为参数),则
(t为参数),则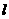 倾斜角为( )
倾斜角为( )
A.20° B.160° C.70° D.110°
12.已知椭圆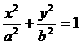 (a>b>0)的一个顶点的坐标为A(0,-1),且右焦点F到直线x-y+2
(a>b>0)的一个顶点的坐标为A(0,-1),且右焦点F到直线x-y+2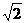 =0的距离为3。(1)已知椭圆的方程(2)是否存在斜率不为0的直线
=0的距离为3。(1)已知椭圆的方程(2)是否存在斜率不为0的直线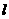 ,使其与已知椭圆交于M、N两点,满足AM⊥AN,且
,使其与已知椭圆交于M、N两点,满足AM⊥AN,且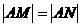 。
。
联想与激活(6)
11.设F1、F2是椭圆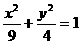 的两个焦点,P为椭圆上的一点。已知P、F1、F2是一个直角三角形的三个顶点,且
的两个焦点,P为椭圆上的一点。已知P、F1、F2是一个直角三角形的三个顶点,且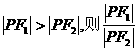 的值为
。
的值为
。
联想:(1)将抛物线y2=4x绕其焦点按逆时针方向旋转90°后,所得抛物线方程为 。
(2)已知抛物线y2=2px(p>0)的焦点在直线y=x-2上,现将抛物线平移,当抛物线的焦点沿直线y=x-2移到点(2a,4a+2)时,所得抛物线的方程为 。
10.设直线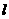 和平面α、β,且
和平面α、β,且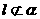 ,
,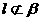 ,给出下列论断:①
,给出下列论断:①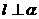 ,②α⊥β,③
,②α⊥β,③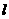 ∥β,从中取两个作为条件,其余的一个为结论,在构成的诸命题中,正确命题的个数是( )
∥β,从中取两个作为条件,其余的一个为结论,在构成的诸命题中,正确命题的个数是( )
A.0 B.1 C.2 D.3
联想:已知α-a-β是大小确定的一个二面角,b和c是空间中的两条直线,下列给出的四个命题条件中,使b和c所成的角为定值的是( )
A.b∥α且c∥β B.b∥α且c⊥β C.b⊥α且c∥β D.b⊥α且c⊥β
9.若(x+1)2n展开式中,x的奇次项系数和与(x+1)n展开式中各项系数和的差为480,则(x+1)2n展开式中的第4项是( )
A.120x2 B.210x4 C.120x7 D.210x6
联想:(1)设(1+x)2+(1+2x)2+(1+3x)2+…+(1+nx)2=a0+a1x+a2x2,则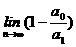 =
。
=
。
(2)已知n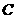
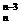 +A
+A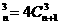 ,则
,则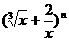 展开式中不含x的项为 。
展开式中不含x的项为 。
8.四个编号分别为1、2、3、4的小球,放入编号分别为1、2、3、4的四个盒子中,每个盒子只放一个球,则有且只有一个小球和盒子的编号相同的概率是( )
A.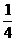 B.
B.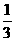 C.
C.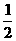 D.
D.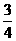
联想:(1)一个口袋中有12个红球,x个白球,每次任取一球,若第10次才取到红球,其概率是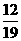 ,则x等于( )
,则x等于( )
A.8 B.7 C.6 D.5
(2)把体育组9个相同的足球放入编号为1,2,3的三个箱子里,要求每个箱子放球的个数不少于其编号数,则不同的放法共有 种。
(3)甲、乙、丙三个单位分别需要招聘工作人员2名、1名、1名,现从10名应聘人员中招聘4个甲、乙、丙三个单位,那么不同的招聘方式共有( )
A.1260种 B.2025种 C.2520种 D.5040种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com