
题目列表(包括答案和解析)
3、在△ABC中,角A、B、C的对边分别为a、b、c,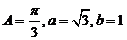 , 则c=( )
, 则c=( )
A)1
B)2
C)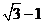 D)
D)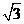
2、复数(4+3i)(4-3i)的值为( )
A)-25i B)25i C)-25 D)25
1、若集合M={x|2x≥4,x∈R},N={x|x2-4x+3=0,x∈R},则M∩N=( )
A){-1,-3} B){1}, C){3} D){1,3}
(17)(本小题满分12分)已知向量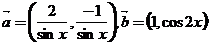 且
且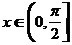 ,
,
(Ⅰ)若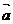 与
与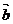 是两个共线向量,求
是两个共线向量,求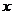 的值;
的值;
(Ⅱ)若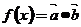 ,求函数
,求函数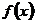 的最小值及相应的
的最小值及相应的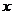 的值。
的值。
(18)(本小题满分12分)杏坛中学组织高二年级4个班的学生到汉方制药厂、贵阳钢厂、贵阳轮胎厂进行社会实践,规定每个班只能在这3个厂中任选择一个,假设每个班选择每个厂的概率是等可能的。
(Ⅰ)求3个厂都有班级选择的概率;
(Ⅱ)求恰有2个厂有班级选择的概率。
(19)(本小题满分12分)已知函数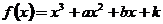 满足
满足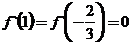 ,
,
(Ⅰ)求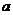 、
、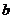 的值及函数
的值及函数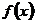 的单调递增区间;
的单调递增区间;
(Ⅱ)若对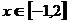 ,不等式
,不等式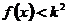 恒成立,求
恒成立,求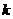 的取值范围。
的取值范围。
(20)(本小题满分12分)如图,已知平面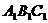 平行于三棱锥
平行于三棱锥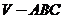 的底面,等边三角形
的底面,等边三角形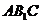 所在平面与面
所在平面与面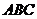 垂直,且
垂直,且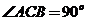 ,设
,设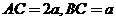 。
。
 (Ⅰ)证明:
(Ⅰ)证明: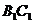 为异面直线
为异面直线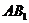 与
与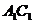 的公垂线;
的公垂线;
(Ⅱ)求点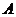 与平面
与平面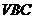 的距离;
的距离;
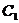
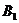
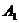 (Ⅲ)求二面角
(Ⅲ)求二面角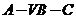 的大小。
的大小。
(21)(本小题满分12分)已知定点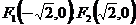 ,动点
,动点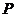 满足条件:
满足条件: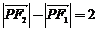 ,点
,点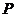 的轨迹是曲线
的轨迹是曲线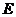 ,直线
,直线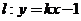 与曲线
与曲线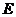 交于
交于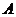 、
、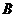 两点。如果
两点。如果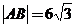 。
。
(Ⅰ)求直线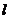 的方程;
的方程;
(Ⅱ)若曲线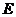 上存在点
上存在点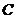 ,使
,使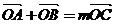 ,求
,求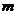 的值。
的值。
(22)(本小题满分12分)已知数列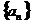 的前
的前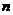 项和为
项和为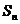 ,
,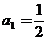 ,且
,且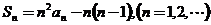
(Ⅰ)写出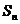 与
与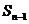 的递推关系式(
的递推关系式(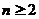 );
);
(Ⅱ)求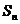 关于
关于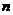 的表达式;
的表达式;
(Ⅲ)设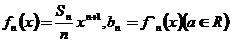 ,求数列
,求数列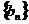 的前
的前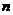 项和
项和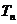 。
。
(13)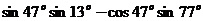 的值为
。
的值为
。
(14)在一次联欢会上,到会的男生比女生多12人。从这些人中随机挑选一人表演节目,若选到女生的概率为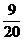 ,则参加联欢会的人数共有
人。
,则参加联欢会的人数共有
人。
(15)若实数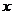 、
、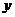 满足
满足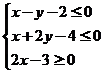 ,则
,则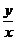 的最大值为
。
的最大值为
。
(16)将正方形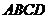 沿对角线
沿对角线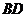 折成直二面角,给出下列四个结论:①
折成直二面角,给出下列四个结论:①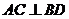 ;②
;②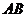 与
与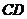 所成角为
所成角为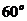 ;③
;③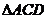 为正三角形;④
为正三角形;④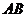 与平面
与平面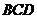 所成角为
所成角为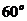 。其中正确的结论是 (填写结论的序号)。
。其中正确的结论是 (填写结论的序号)。
(1)已知集合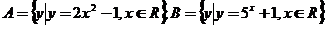 ,则
,则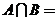
(A)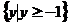 (B)
(B)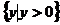 (C)
(C)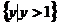 (D)
(D)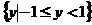
(2)在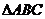 中,角
中,角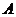 、
、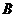 、
、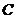 的对边分别是
的对边分别是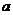 、
、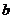 、
、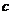 ,若
,若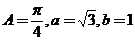 ,则
,则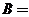
(A)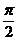 (B)
(B)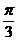 (C)
(C)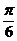 (D)
(D)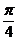
(3)已知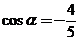 且
且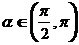 ,则
,则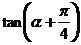 等于
等于
(A)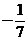 (B)
(B)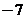 (C)
(C)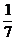 (D)7
(D)7
(4)已知向量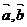 满足
满足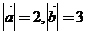 ,且
,且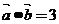 ,则
,则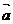 与
与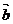 的夹角为
的夹角为
(A)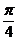 (B)
(B)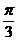 (C)
(C)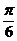 (D)
(D)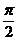
(5)若数列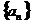 中,
中,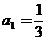 ,且对任意的正整数
,且对任意的正整数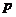 、
、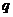 都有
都有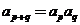 ,则
,则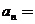
(A)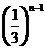 (B)
(B)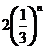 (C)
(C) (D)
(D)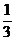
(6)若直线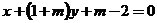 与直线
与直线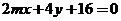 平行,则
平行,则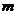 的值等于
的值等于
(A) 1 (B)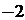 (C)1或
(C)1或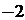 (D)
(D)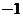 或
或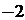
(7)曲线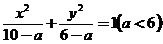 与曲线
与曲线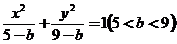 有
有
(A)相同的焦距 (B)相同的离心率 (C)相同的焦点 (D)相同的准线
(8)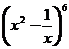 的展开式中的常数项是
的展开式中的常数项是
(A)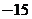 (B)15 (C)
(B)15 (C)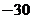 (D)30
(D)30
(9)函数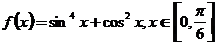 的最小值是
的最小值是
(A)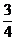 (B)
(B)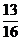 (C)
(C)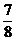 (D)1
(D)1
(10)对于任意的直线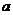 与平面
与平面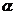 ,在平面
,在平面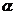 内必有直线
内必有直线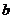 ,使直线
,使直线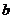 与
与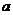
(A)平行 (B)相交 (C)互为异面直线 (D)垂直
(11)若不等式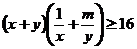 对任意的
对任意的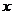 、
、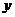 恒成立,则正实数
恒成立,则正实数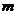 的最小值为
的最小值为
(A)1 (B)4 (C)9 (D)14
(12)若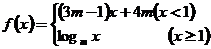 是
是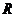 上的减函数,那么
上的减函数,那么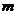 的的取值范围是
的的取值范围是
(A)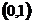 (B)
(B)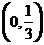 (C)
(C)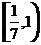 (D)
(D)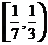
21.(本小题满分13分)
已知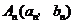 (
(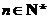 )是曲线
)是曲线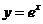 上的点,
上的点,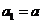 ,
,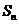 是数列
是数列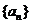 的前
的前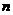 项和,且满足
项和,且满足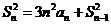 ,
,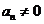 ,
,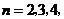 ….
….
(I)证明:数列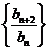 (
(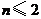 )是常数数列;
)是常数数列;
(II)确定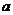 的取值集合
的取值集合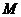 ,使
,使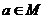 时,数列
时,数列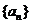 是单调递增数列;
是单调递增数列;
(III)证明:当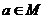 时,弦
时,弦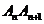 (
(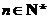 )的斜率随
)的斜率随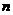 单调递增.
单调递增.
2007年普通高等学校招生全国统一考试(湖南卷)
20.(本小题满分12分)
已知双曲线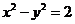 的左、右焦点分别为
的左、右焦点分别为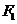 ,
,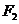 ,过点
,过点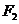 的动直线与双曲线相交于
的动直线与双曲线相交于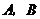 两点.
两点.
(I)若动点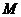 满足
满足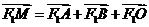 (其中
(其中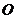 为坐标原点),求点
为坐标原点),求点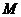 的轨迹方程;
的轨迹方程;
(II)在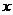 轴上是否存在定点
轴上是否存在定点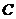 ,使
,使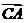 ·
·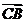 为常数?若存在,求出点
为常数?若存在,求出点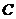 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
19.(本小题满分12分)
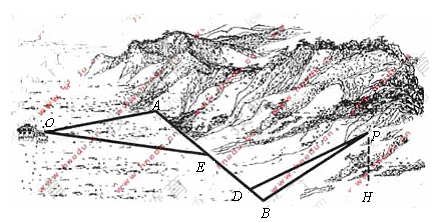
如图4,某地为了开发旅游资源,欲修建一条连接风景点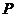 和居民区
和居民区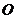 的公路,点
的公路,点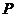 所在的山坡面与山脚所在水平面
所在的山坡面与山脚所在水平面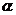 所成的二面角为
所成的二面角为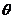 (
( ),且
),且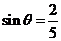 ,点
,点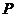 到平面
到平面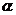 的距离
的距离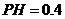 (km).沿山脚原有一段笔直的公路
(km).沿山脚原有一段笔直的公路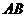 可供利用.从点
可供利用.从点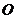 到山脚修路的造价为
到山脚修路的造价为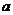 万元/km,原有公路改建费用为
万元/km,原有公路改建费用为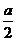 万元/km.当山坡上公路长度为
万元/km.当山坡上公路长度为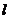 km(
km(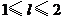 )时,其造价为
)时,其造价为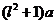 万元.已知
万元.已知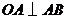 ,
,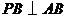 ,
,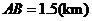 ,
,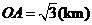 .
.
(I)在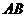 上求一点
上求一点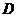 ,使沿折线
,使沿折线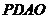 修建公路的总造价最小;
修建公路的总造价最小;
(II) 对于(I)中得到的点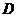 ,在
,在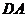 上求一点
上求一点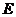 ,使沿折线
,使沿折线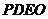 修建公路的总造价最小.
修建公路的总造价最小.
(III)在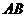 上是否存在两个不同的点
上是否存在两个不同的点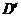 ,
,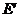 ,使沿折线
,使沿折线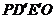 修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.

18.(本小题满分12分)
如图2,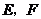 分别是矩形
分别是矩形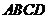 的边
的边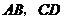 的中点,
的中点,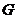 是
是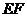 上的一点,将
上的一点,将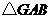 ,
,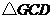 分别沿
分别沿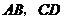 翻折成
翻折成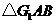 ,
,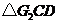 ,并连结
,并连结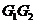 ,使得平面
,使得平面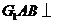 平面
平面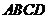 ,
,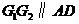 ,且
,且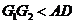 .连结
.连结 ,如图3.
,如图3.
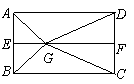

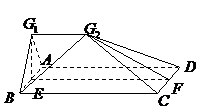

图2 图3
(I)证明:平面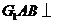 平面
平面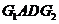 ;
;
(II)当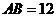 ,
,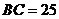 ,
,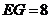 时,求直线
时,求直线 和平面
和平面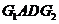 所成的角.
所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com