
题目列表(包括答案和解析)
4.把函数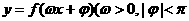 )的图象向左平移
)的图象向左平移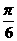 个单位,再将图象上所有点的 横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上所有点的 横坐标伸长到原来的2倍(纵坐标不变),得到函数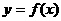 的图象,则 ( )
的图象,则 ( )
A.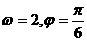 B.
B.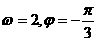
C.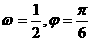 D.
D.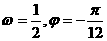
3.若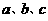 是常数,则“
是常数,则“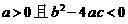 ”是“对任意
”是“对任意 ,有
,有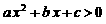 ”的 ( )
”的 ( )
A.充分不必要条件. B.必要不充分条件.
C.充要条件. D.既不充分也不必要条件.
2.在等差数列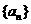 中,若
中,若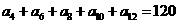 ,则
,则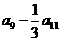 的值为 ( )
的值为 ( )
A.14 B.15 C.16 D.17
1、将函数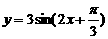 的图象按向量
的图象按向量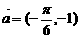
平移后所得图象的解析式是( )
A.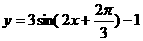 B.
B.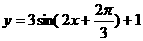
C.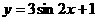 D.
D.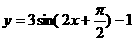
21.(14分)已知函数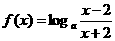 的定义域为[
的定义域为[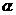 ,
,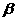 ],值域为
],值域为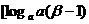 ,
,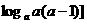 ,并且
,并且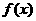 在
在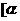 ,
,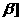 上为减函数.
上为减函数.
(1)求a的取值范围;
(2)求证: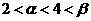 ;
;
20.(14分)某地区预计明年从年初开始的前x个月内,对某种商品的需求总量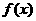 (万件)与月份x的近似关系为:
(万件)与月份x的近似关系为: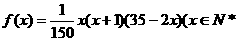 ,且
,且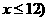 .
.
(1)写出明年第x个月的需求量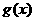 (万件)与月x的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?
(万件)与月x的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?
(2)如果将该商品每月都投放市场p万件(销售未完的商品都可以在以后各月销售),要保证每月都足量供应,问:p至少为多少万件?
19.(14分)在抛物线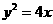 上存在两个不同的点关于直线l;y=kx+3对称,求k的取值范围.
上存在两个不同的点关于直线l;y=kx+3对称,求k的取值范围.
18.(14分)(甲)如图,已知斜三棱柱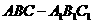 的侧面
的侧面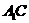 ⊥底面ABC,∠ABC=90°,BC=2,AC=
⊥底面ABC,∠ABC=90°,BC=2,AC=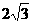 ,又
,又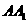 ⊥
⊥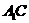 ,
,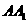 =
=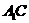 .
.
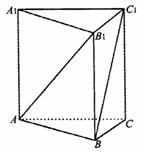
(1)求侧棱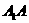 与底面ABC所成的角的大小;
与底面ABC所成的角的大小;
(2)求侧面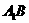 与底面所成二面角的大小;
与底面所成二面角的大小;
(3)求点C到侧面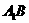 的距离.
的距离.
(乙)在棱长为a的正方体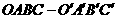 中,E,F分别是棱AB,BC上的动点,且AE=BF.
中,E,F分别是棱AB,BC上的动点,且AE=BF.
(1)求证: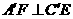 ;
;
(2)当三棱锥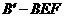 的体积取得最大值时,求二面角
的体积取得最大值时,求二面角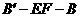 的大小(结果用反三角函数表示).
的大小(结果用反三角函数表示).
17.(12分)无穷数列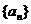 的前n项和
的前n项和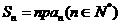 ,并且
,并且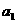 ≠
≠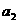 .
.
(1)求p的值;
(2)求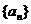 的通项公式;
的通项公式;
16.(12分)设函数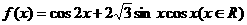 的最大值为M,最小正周期为T.
的最大值为M,最小正周期为T.
(Ⅰ)求M、T;
(Ⅱ)10个互不相等的正数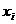 满足
满足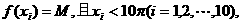 求
求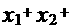 … +
… +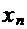 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com