
题目列表(包括答案和解析)
1. 点到直线距离公式及证明
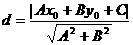
关于证明:
根据点斜式,直线PQ的方程为(不妨设A≠0)
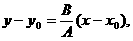
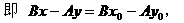
解方程组
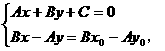
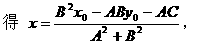
这就是点Q的横坐标,又可得
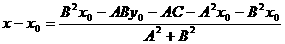
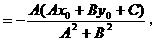
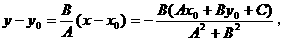
所以,
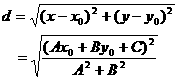
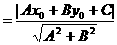 。
。
这就推导得到点P(x0,y0)到直线l:Ax+By+C=0的距离公式。
如果A=0或B=0,上式的距离公式仍然成立。
下面再介绍一种直接用两点间距离公式的推导方法。
设点Q的坐标为(x1,y1),则
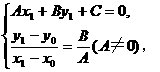
把方程组作变形,
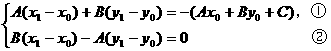
把①,②两边分别平方后相加,得
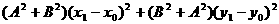
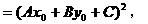
所以,
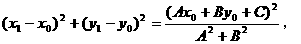
所以,
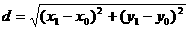
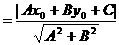
此公式还可以用向量的有关知识推导,介绍如下:

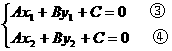
把③、④两式左右两边分别相减,得
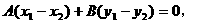
由向量的数量积的知识,知
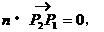
这里n=(A,B)。所以n=(A,B)是与直线l垂直的向量。
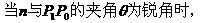
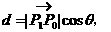
(如图所示)
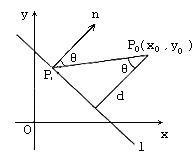

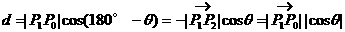
(如图所示)
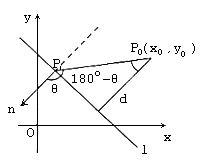
所以,都有

因为
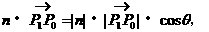
所以
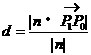
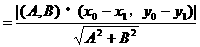
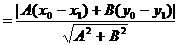
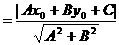
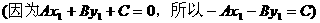
点到直线的距离;
点关于点、关于直线的对称点;
直线关于点、关于直线的对称直线;
直线方程复习;
22.数列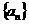 的前
的前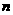 项和
项和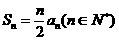 ,且
,且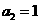 ,
,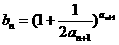 (
(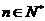 ).
).
(1)求数列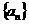 的通项;
的通项;
(2)已知定理:
“若函数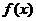 在区间
在区间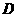 上是凹函数,
上是凹函数,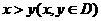 ,且
,且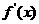 存在,则有
存在,则有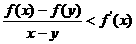 ”。若函数
”。若函数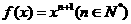 在
在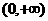 上是凹函数,试判断
上是凹函数,试判断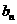 与
与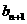 的大小; (3)求证:
的大小; (3)求证: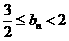 .
.
21.已知函数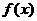 的定义域为I,导数
的定义域为I,导数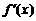 满足0<
满足0<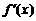 <2 且
<2 且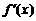 ≠1,常数c1为方程
≠1,常数c1为方程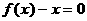 的实数根,常数c2为方程
的实数根,常数c2为方程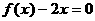 的实数根.
的实数根.
(I)若对任意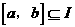 ,存在
,存在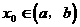 ,使等式
,使等式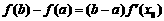 成立.试问:方程
成立.试问:方程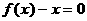 有几个实数根;
有几个实数根;
(II)求证:当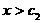 时,总有
时,总有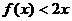 成立;
成立;
(III)对任意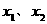 ,若满足
,若满足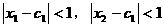 ,求证:
,求证: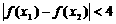 .
.
20.某汽车厂有一条价值为a万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值.经过市场调查,产品的增加值y万元与技术改造投入x万元之间满足:①y与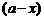 和
和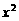 的乘积成正比;②当
的乘积成正比;②当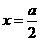 时,y=
时,y=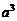 .并且技术改造投入比率:
.并且技术改造投入比率: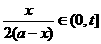 ,其中t是常数,且
,其中t是常数,且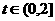 .
.
(1)设y=f(x),求f(x)的表达式及定义域;
(2)求出产品增加值y的最大值及相应的x的值.
19.已知正项数列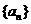 满足
满足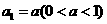 ,且
,且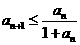 .求证(1)
.求证(1)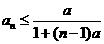 ; (2)
; (2)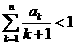
18.在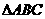 中,
中,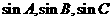 构成公差为正数的等差数列,且其周长为12,以
构成公差为正数的等差数列,且其周长为12,以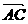 为x轴,
为x轴, 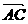 的中垂线为 y轴,建立直角坐标系,
的中垂线为 y轴,建立直角坐标系,
(1)证明存在两定点E,F,使得|BE|+|BF|为定长;并求出点E,F的坐标及点B的轨迹C;
(2)设P为轨迹C
上的任一点,点M,N分别在射线PA,PC上,动点Q满足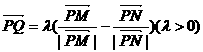 ,经过点A且以
,经过点A且以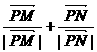 为方向向量的直
为方向向量的直
与动点Q的轨迹交于点R
,试问:是否存在一个定点 D,使得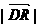 为定值?若存在求出点D的坐标;若不存在,说明理由?
为定值?若存在求出点D的坐标;若不存在,说明理由?
17.一个截面为抛物线形的旧河道,河口宽4米,河深2米,现要将其截面2改造为等腰梯形,要求河道深度不变,而且施工时只能挖土,不准向河道填土,试求当截面梯形的下底长为多少米时,才能使挖出的土最少?
16.已知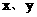 之间满足
之间满足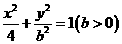 ,动点(x,y)在曲线
,动点(x,y)在曲线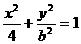 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;
15.用硬纸剪出一个三边均不等的锐角三角形 ,然后以
,然后以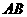 边上的高
边上的高 为折痕,折得两个直角三角形,使之直立于桌面上,那么,
为折痕,折得两个直角三角形,使之直立于桌面上,那么, 就是角
就是角 在桌面上的射影,转动其中的一个直角三角形,观察
在桌面上的射影,转动其中的一个直角三角形,观察 与
与 的大小关系,并说明理由
的大小关系,并说明理由
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com