
题目列表(包括答案和解析)
6.已知椭圆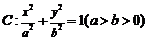 ,顺次连结椭圆
,顺次连结椭圆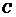 的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率
的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率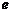 等于( ).
等于( ).
A.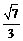 B.
B.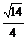 C.
C.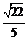 D.
D.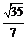
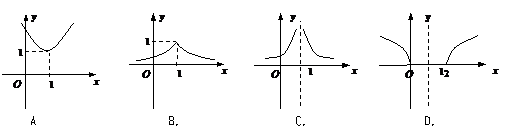 7.若实数
7.若实数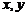 满足
满足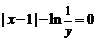 ,则
,则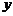 关于
关于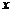 的函数的图象大致是( ).
的函数的图象大致是( ).
5.若点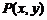 在以
在以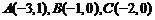 为顶点的
为顶点的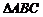 的内部运动(不包含边界),则
的内部运动(不包含边界),则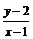 的取值范围( ).
的取值范围( ).
A.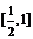 B.
B.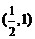 C.
C.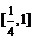 D.
D.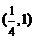
4.若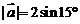 ,
,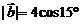 ,
,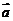 与
与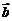 的夹角为
的夹角为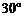 ,则
,则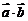 的值为( ).
的值为( ).
A. 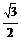 B.
B.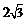 C.
C.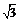 D.
D.
3.函数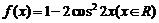 是( ).
是( ).
A.最小正周期为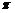 的偶函数
B.最小正周期为
的偶函数
B.最小正周期为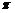 的奇函数
的奇函数
C.最小正周期为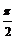 的偶函数
D.最小正周期为
的偶函数
D.最小正周期为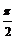 的偶函数
的偶函数
2.已知函数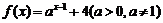 的反函数
的反函数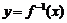 的图象经过一个定点,则这个定点的坐
的图象经过一个定点,则这个定点的坐
标为( ).
A.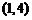 B.
B.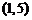 C.
C.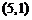 D.
D.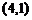
1.复数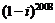 的实部为( ).
的实部为( ).
A.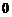 B.
B.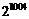 C.
C.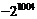 D.
D.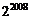
22、(本小题满分13分)已知椭圆C: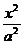 +
+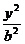 =1(a>b>0)的左、右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴、y轴分别交于点A、B ,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左、右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴、y轴分别交于点A、B ,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设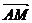 =λ
=λ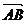 .
.
(Ⅰ)证明:λ=1- e2;
(Ⅱ)若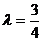 ,△PF1F2的周长为6;写出椭圆C的方程.
,△PF1F2的周长为6;写出椭圆C的方程.
21.(本小题满分13分)已知函数f(x)=-x3+ax2+b的图象上任意两点连线的斜率都小于1.
(Ⅰ)判断函数g(x)=f(x)-x的单调性,并加以证明;
(Ⅱ)求实数a的取值范围.
20.(12分)已知数列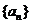 的前
的前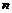 项和
项和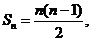 且
且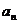 是
是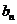 和
和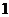 的等差中项。(1)求数列
的等差中项。(1)求数列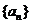 和
和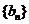 的通项公式;(2)若
的通项公式;(2)若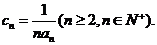 求
求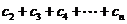 ;(3)若
;(3)若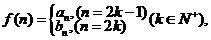 是否存在
是否存在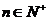 使得
使得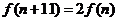 ?若存在,求出
?若存在,求出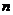 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
19.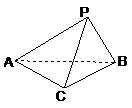 (12分)如图,已知三棱锥
(12分)如图,已知三棱锥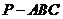 中,
中,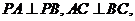 平面
平面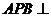 平面
平面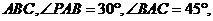
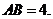 (1)求二面角
(1)求二面角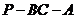 的大小;(2)若
的大小;(2)若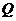 为棱
为棱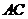 上的一动点,则直线
上的一动点,则直线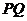 与底面
与底面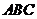 能否成
能否成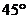 的角?若能,求出点
的角?若能,求出点 的位置;若不能,说明理由。
的位置;若不能,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com