
题目列表(包括答案和解析)
1.函数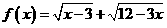 的值域为( )
的值域为( )
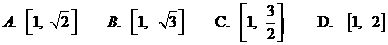
解: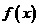 的定义域为
的定义域为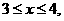 则
则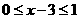 ,令
,令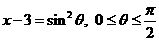 ,则
,则
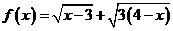
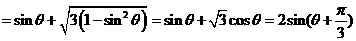
因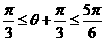 ,则
,则 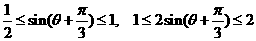 .
.
故选D
7.已知A(2cos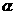 ,
,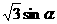 ),B(2cos
),B(2cos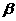 ,
,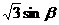 ),C(-1,0)是平面上三个不同的点,若存在
),C(-1,0)是平面上三个不同的点,若存在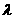 ,使得
,使得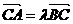 ,试求
,试求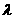 的取值范围。
的取值范围。
解:由已知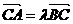 ,可得
,可得
(2cos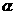 +1,
+1, 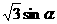 )=
)=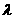 (-1-2cos
(-1-2cos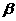 ,-
,-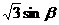 ),
),
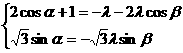 ,
,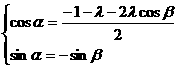 ,
,
由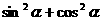 =1,得
=1,得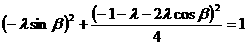 ,
,
即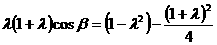 ,
,
若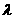 =-1,则
=-1,则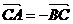 ,得
,得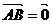 ,这与A,B两点不重合矛盾,
,这与A,B两点不重合矛盾,
因此,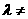 -1,于是
-1,于是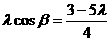 ,可知
,可知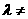 0,
0,
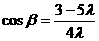 ,得
,得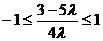 ,
,
解得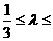 3。
3。
6.已知常数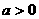 ,经过定点A(0,-a)以(l,a)为方向向量的直线与经过定点B(0,a)以(1,-2la)为方向向量的直线相交于点P,其中
,经过定点A(0,-a)以(l,a)为方向向量的直线与经过定点B(0,a)以(1,-2la)为方向向量的直线相交于点P,其中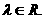 试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
试问:是否存在两个定点E、F,使得|PE|+|PF|为定值.若存在,求出E、F的坐标;若不存在,说明理由.
解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
因此,直线AP和BP的方程为
l(y+a)=ax 和 y-a=-2lax.
消去参数l,得点P(x,y)的坐标满足方程y2-a2=-2a2x2,
整理得 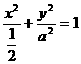 . ①
. ①
因为a>0,所以得:
(ⅰ)当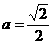 时,方程①是圆方程,故不存在合乎题意的定点E和F;
时,方程①是圆方程,故不存在合乎题意的定点E和F;
(ⅱ)当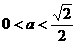 时,方程①表示椭圆,焦点
时,方程①表示椭圆,焦点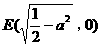 和
和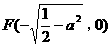 为合乎题意的两个定点:
为合乎题意的两个定点:
(ⅲ)当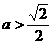 时,方程①也表示椭圆,焦点
时,方程①也表示椭圆,焦点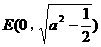 和
和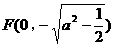 为合乎题意的两个定点.
为合乎题意的两个定点.
5.过椭圆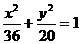 的一个焦点 F作弦AB,则
的一个焦点 F作弦AB,则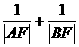 =
。
=
。
解:不妨设焦点F为右焦点,则F(4,0)。当AB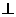 x轴时,A(4,
x轴时,A(4,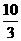 ),B(4,-
),B(4,-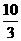 )
)
所以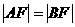 =
=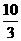 ,故
,故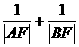 =
=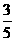
4.椭圆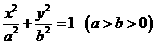 的中心,右焦点,右顶点,右准线与
的中心,右焦点,右顶点,右准线与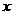 轴的交点依次为
轴的交点依次为
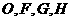 ,则
,则 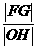 的最大值为( ).
的最大值为( ).
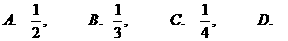 不能确定.
不能确定.
答: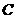 .
.
解: 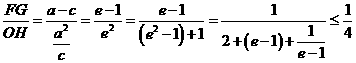 .(
.(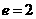 时取等号)
时取等号)
3.设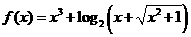 ,则对任意实数
,则对任意实数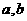 ,
,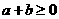 是
是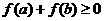 的( A )
的( A )
A. 充分必要条件 B. 充分而不必要条件
C. 必要而不充分条件 D. 既不充分也不必要条件
解:显然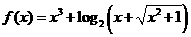 为奇函数,且单调递增。于是
为奇函数,且单调递增。于是
若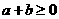 ,则
,则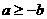 ,有
,有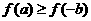 ,即
,即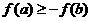 ,从而有
,从而有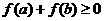 .
.
反之,若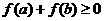 ,则
,则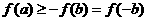 ,推出
,推出 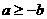 ,即
,即 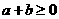 。
。
故选A。
2.手表的表面在一平面上。整点1,2,…,12这12个数字等间隔地分布在半径为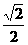 的圆周上。从整点i到整点(i+1)的向量记作
的圆周上。从整点i到整点(i+1)的向量记作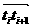 ,则
,则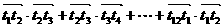 =
= 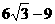 。
。
解:连接相邻刻度的线段构成半径为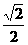 的圆内接正12边形。相邻两个边向量的夹角即为正12边形外角,为30度。各边向量的长为
的圆内接正12边形。相邻两个边向量的夹角即为正12边形外角,为30度。各边向量的长为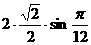
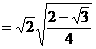 。 则
。 则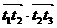
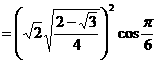
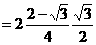 。共有12个相等项。所以求得数量积之和为
。共有12个相等项。所以求得数量积之和为 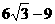 。
。
1. 函数 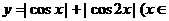 R) 的最小值是
.
R) 的最小值是
.
解:令 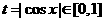 ,则
,则 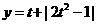 .
.
当 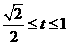 时,
时, 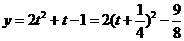 ,得
,得 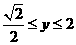 ;
;
当 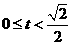 时,
时, 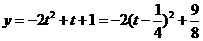 ,得
,得 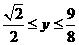
又 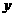 可取到
可取到 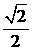 , 故填
, 故填 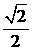 .
.
6、已知函数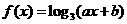 的图像经过点
的图像经过点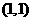 和点
和点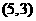 ,且数列
,且数列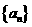 满足
满足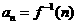 ,记数列
,记数列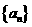 的前
的前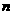 项和为
项和为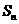 (
(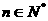 ).
).
(1)求数列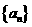 的通项公式;
的通项公式;
(2)设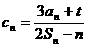 ,且数列
,且数列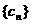 为递增数列,即对
为递增数列,即对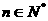 ,恒有
,恒有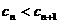 成立,试求
成立,试求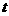 的取值范围;
的取值范围;
解:(1)由条件,得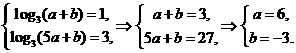
于是,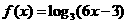 ,
,
则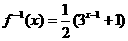 ,
,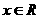 .
.
又因为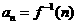 ,所以数列
,所以数列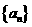 的通项公式为
的通项公式为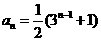 ,
,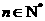 .
.
(2)因为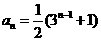 ,所以
,所以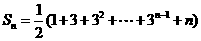
即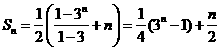 .
.
于是,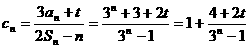 ,因为
,因为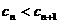 ,所以
,所以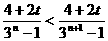 ,
,
因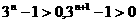 ,则
,则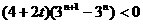
所以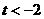 .
.
5、抛物线的顶点在原点,焦点在x轴的正半轴上,直线x+y-1=0与抛物线相交于A、B两点,且|AB|=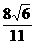 .
.
(1)求抛物线的方程;
(2)在x轴上是否存在一点C,使△ABC为正三角形?若存在,求出C点的坐标:若不存在,请说明理由。
解:(1)设所求抛物线方程为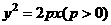 ,
,
则由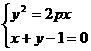 消支y得 x2-2(1+p)x+1=0
消支y得 x2-2(1+p)x+1=0
设A(x1,y1)、B(x2,y2)
则x1+ x2=2(1+p) x1x2=1
由弦长|AB|=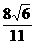 建立关于p的方程.
建立关于p的方程.
解得 p=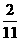 或p=-
或p=-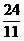 (舍去)
(舍去)
故抛物线方程为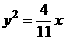 .
.
(2)设AB的中点为D则D(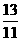 ,-
,-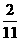 ),x轴上存在满足条件的点C(x0,0),
),x轴上存在满足条件的点C(x0,0),
由于△ABC为正三角形.所以CD⊥AB,|CD|=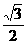 |AB|=
|AB|=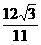 .
.
由CD⊥AB得x0=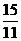 但|CD|=
但|CD|=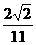
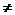
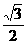 |AB|=
|AB|=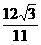
故x轴上不存在点C,使△ABC为正三角形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com