
题目列表(包括答案和解析)
18、解:(I)由题意知: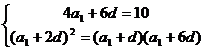
解得: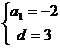 或
或 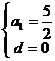
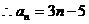 或
或 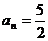
(II)当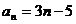 时,数列
时,数列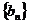 是首项为
是首项为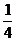 ,公比为8等比数列,
,公比为8等比数列,
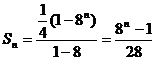
当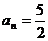 时,
时,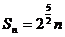
综上,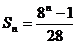 或
或 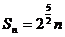
19解:(I) 抛物线与直线有两不同的交点,
抛物线与直线有两不同的交点,
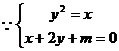 有两个不同的解,即方程
有两个不同的解,即方程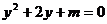 有两个不同的解
有两个不同的解 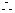
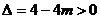 即:
即: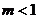
(I)
设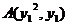 ,(
,(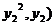 ,
,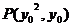 ,
,
由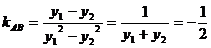 得
得 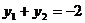
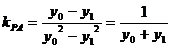
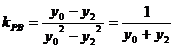
假设在抛物线上存在定点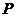 使得直线
使得直线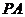 与
与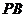 的斜率互为相反数。
的斜率互为相反数。
即: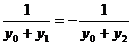 即:
即: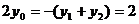 得
得 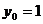
即:存在定点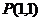 使得直线
使得直线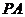 与
与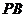 的斜率互为相反数。
的斜率互为相反数。
17.解:当甲真时,设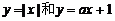
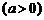 ,即两函数图象有两个交点.
,即两函数图象有两个交点.
则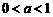
当乙真时,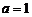 时 满足 或
时 满足 或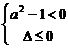 也满足
也满足
则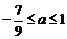
∴当甲乙有但仅有一个为真命题时,即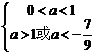 或
或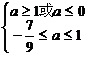
∴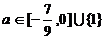
16.解:(1)在△ABC中有B+C=π-A,由条件可得 4[1-cos(B+C)]-4cos2A+2=7.
又∵ cos(B+C)=-cosA, ∴4 cos2A-4cosA+1=0
解得:cosA=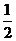 , 又A∈(0,π),∴ A=
, 又A∈(0,π),∴ A=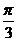 .
.
(2)由cosA=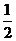 知
知 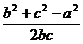 =
=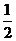 , 即
, 即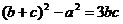 .
.
又a=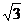 ,b+c=3,代入得
,b+c=3,代入得 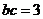 .
.
由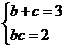
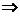
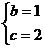 或
或 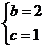
11.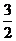 ; 12。120°; 13.
; 12。120°; 13.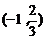 ; 14。
; 14。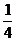 ; 15.
; 15.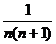 。
。
BDCCA、DABCA
21、(14分)已知函数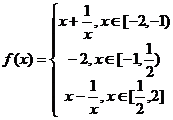
(I)求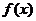 的值域;
的值域;
(II)设函数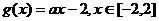 ,若对于任意
,若对于任意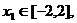 总存在
总存在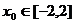 ,使得
,使得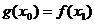 成立,求实数
成立,求实数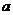 的取值范围。
的取值范围。
(文科)2答案
YCY
20.(14分)
已知定义在R上的函数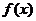 满足:对于任意实数
满足:对于任意实数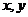 ,恒有
,恒有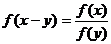 ,且当
,且当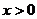 时,
时,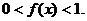
(1)求证: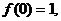 当
当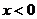 时,有
时,有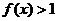 ;
;
(2)试判断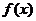 在且R上的单调性,并证明你的结论;
在且R上的单调性,并证明你的结论;
(3)若实数x、y满足: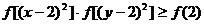 ,且
,且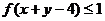 ,
,
求z=x+y的取值范围.
19、(14分)已知直线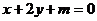
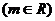 与抛物线
与抛物线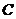 :
: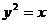 相交于不同的两点A,B
相交于不同的两点A,B
(I)求实数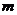 的取值范围;
的取值范围;
(II)在抛物线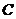 上是否存在一个定点
上是否存在一个定点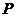 ,对(I)中任意的
,对(I)中任意的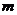 的值,都有直线
的值,都有直线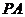 与
与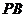 的斜率互为相反数?若存在,求出点
的斜率互为相反数?若存在,求出点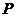 的坐标;若不存在,试说明理由
的坐标;若不存在,试说明理由
 学校_________________班级
姓名
学号 学校_________________班级
姓名
学号
|
18、(14分)已知等差数列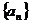 的前4项的和为10,且
的前4项的和为10,且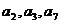 成等比数列。
成等比数列。
(I)求通项公式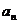 。
。
(II)设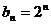 ,求数列
,求数列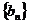 的前
的前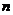 项的和
项的和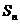 。
。
17. (12分) 命题甲: 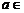 R, 关于x的方程
R, 关于x的方程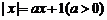 有两个非零实数解; 命题乙:
有两个非零实数解; 命题乙:
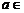 R, 关于x的不等式
R, 关于x的不等式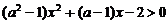 的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com