
题目列表(包括答案和解析)
1.若集合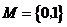 ,
,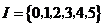 ,则
,则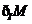 为( )
为( )
A.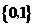 B.
B.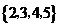 C.
C.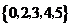 D.
D.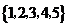
22、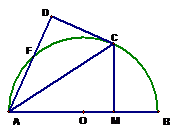 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M。(1)求证:DC是⊙O的切线;(2)求证:AM·MB=DF·DA。
B、选修4-4:坐标系与参数方程
已知圆锥曲线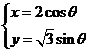 (
(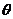 是参数)和定点A(0,
是参数)和定点A(0,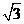 ),F1、F2是圆锥曲线的左、右焦点。
),F1、F2是圆锥曲线的左、右焦点。
(1)求经过点F1垂直于直线AF2的直线l的参数方程;(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。
C、选修4-5:不等式选讲
对于任意的实数a(a≠0)和b,不等式|a+b|+|a-b|≥|a|(|x-1|+|x-2|)恒成立,求实数x的取值范围。
21、已知数列{an}的前n项和为Sn,函数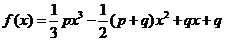 (其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N*)均在函数
(其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N*)均在函数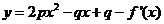 的图象上(其中是
的图象上(其中是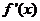 函数f(x)的导函数)。
函数f(x)的导函数)。
(1)求a1的值;(2)求数列{an}的通项公式;(3)记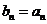 ·
·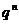 ,求数列{bn}的前n项和Tn。
,求数列{bn}的前n项和Tn。
20、已知点C为圆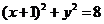 的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且
的圆心,点A(1,0),P是圆上的动点,点Q在圆的半径CP上,且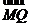 ·
·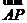 =0,
=0,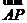 =2
=2 。
。
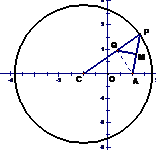 (1)当点P在圆上运动时,求点Q的轨迹方程;(2)若直线
(1)当点P在圆上运动时,求点Q的轨迹方程;(2)若直线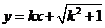 与(1)中所求点Q的轨迹交于不同两点F、H,O是坐标原点,且
与(1)中所求点Q的轨迹交于不同两点F、H,O是坐标原点,且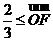 ·
·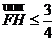 时,求△FOH面积的取值范围。
时,求△FOH面积的取值范围。
19、班主任为了对本班学生的考试成绩进行分析,决定从全班25名女同学,15名男同学中随机抽取一个容量为8的样本进行分析。(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出算式即可,不必计算出结果);
(Ⅱ)随机抽取8位,他们的数学分数从小到大排序是:60、65、70、75、80、85、90、95,物理分数从小到大排序是:72、77、80、84、88、90、93、95。
(1)若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;(2)若这8位同学的数学、物理分数事实上对应如下表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
数学分数x |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
|
物理分数y |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?如果具有线性相关性,求y与x的线性回归方程(系数精确到0.01),如果不具有线性相关性,请说明理由。
参考公式:相关系数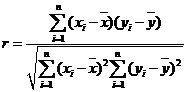 ;回归直线的方程是:
;回归直线的方程是: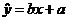 ,
,
其中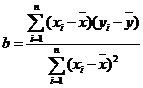 ,
,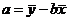 ;其中
;其中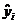 是与
是与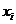 对应的回归估计值。
对应的回归估计值。
参考数据: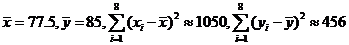 ,
,
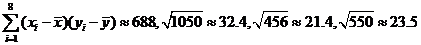
18、 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=PB=1,AD=
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=PB=1,AD=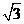 ,点F是PB的中点,点E在边BC上移动。
,点F是PB的中点,点E在边BC上移动。
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)证明:无论点E在BC边的何处,都有PE⊥AF;
(3)当BE等于何值时,PA与平面PDE所成角的大小为45°。
解:(1) 点E为BC的中点时, EF∥平面PAC。
证明如下:∵BE=CE,BF=PF ∴EF∥PC
又EF在平面PAC外,PC在平面PAC内,所以EF∥平面PAC
(2) ∵PA=AB,BF=PF ∴AF⊥PB ∵PA⊥平面ABCD ∴PA⊥BC
又BC⊥AB ∴BC⊥平面PAB 而AF在平面PAB内,∴AF⊥BC
 ∵BC、PB是平面PBC内的两条相交直线 ∴AF⊥平面PBC
∵BC、PB是平面PBC内的两条相交直线 ∴AF⊥平面PBC
∵无论点E在BC边的何处,PE都在平面PBC内 ∴PE⊥AF
(3)利用空间向量来解。以A为原点,AD、AB、AP所在的直线分别为x轴、y轴、z轴,建立空间直角坐标系A-xyz。设BE=m,
则A(0,0,0),P(0,0,1),D(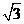 ,0,0),E(m,1,0),
,0,0),E(m,1,0),
∴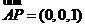 ,
,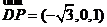 ,
,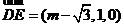 ,
,
设平面PDE的法向量为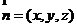 ,则
,则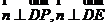 ,
,
∴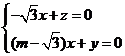 ,
,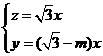 ,令x=1,得
,令x=1,得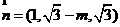 ,
,
∵PA与平面PDE所成角的大小为45° ∴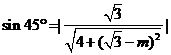 ,
,
解得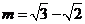 或
或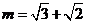 (舍)
(舍)
因此,当BE=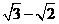 时,PA与平面PDE所成角的大小为45°。
时,PA与平面PDE所成角的大小为45°。
17、设向量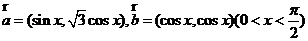 。
。
(1)若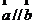 ,求tanx的值;(2)求函数
,求tanx的值;(2)求函数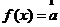 ·
·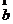 的最大值及相应x的值。
的最大值及相应x的值。
16、如果函数f(x)同时满足下列条件:①过点(0,-1)和(1,-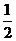 );②在[0,+∞)上递增;③随着x值的增大,f(x)的图象无限接近x轴,但与x轴不相交,那么f(x)的一个函数解析式可能是___________________。
);②在[0,+∞)上递增;③随着x值的增大,f(x)的图象无限接近x轴,但与x轴不相交,那么f(x)的一个函数解析式可能是___________________。
14、“好运”出租车公司按月将某辆车出租给司机,按照规定:无论是否出租,该公司每月都要负担这辆车的各种管理费100元,如果在一月内该车被租的概率是0.8,租金是2600元,那么公司每月对这辆车收支的期望值为________元。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com