
题目列表(包括答案和解析)
8.已知曲线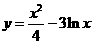 的一条切线的斜率为,则切点的横坐标为
的一条切线的斜率为,则切点的横坐标为
(A)3 (B) 2 (C) 1 (D)
7.已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦等于
(A) 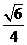 (B)
(B)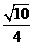 (C)
(C) 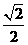 (D)
(D) 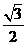
6.不等式: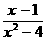 >0的解集为
>0的解集为
(A)( -2, 1) (B) ( 2, +∞)
(C) ( -2, 1)∪ ( 2, +∞) (D) ( -∞, -2)∪ ( 1, +∞)
5.在∆ABC中,已知D是AB边上一点,若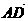 =2
=2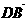 ,
,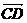 =
=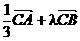 ,则l=
,则l=
(A)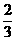 (B)
(B)
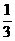 (C) -
(C) -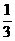 (D)
-
(D)
-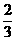
4.以下四个数中的最大者是
(A) (ln2)2 (B)
ln(ln2) (C)
ln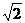 (D)
ln2
(D)
ln2
3.设复数z满足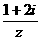 =i,则z =
=i,则z =
(A) -2+i (B) -2-i (C) 2-i (D) 2+i
2.函数f(x)=|sinx|的一个单调递增区间是
(A)(-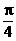 ,
,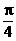 ) (B) (
) (B) (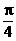 ,
,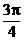 ) (C)
(p,
) (C)
(p,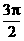 ) (D) (
) (D) (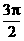 ,2p)
,2p)
1. sin2100 =
(A)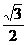 (B)
-
(B)
-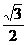 (C)
(C)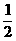 (D)
-
(D)
-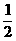
20.(本小题满分14分)
设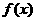 是定义在
是定义在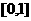 上的函数,若存在
上的函数,若存在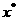
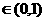 ,使得
,使得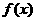 在
在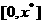 上单调递增,在
上单调递增,在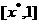 上单调递减,则称
上单调递减,则称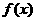 为
为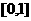 上的单峰函数,
上的单峰函数,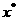 为峰点,包含峰点的区间为含峰区间. 对任意的
为峰点,包含峰点的区间为含峰区间. 对任意的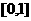 上的单峰函数
上的单峰函数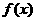 ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.
(1)证明:对任意的
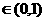 ,
, ,若
,若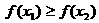 ,则
,则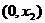 为含峰区间;若
为含峰区间;若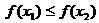 ,则
,则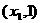 为含峰区间;
为含峰区间;
(2)对给定的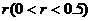 ,证明:存在
,证明:存在
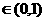 ,满足
,满足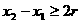 ,使得由(1)所确定的含峰区间的长度不大于
,使得由(1)所确定的含峰区间的长度不大于 ;
;
19.(本小题满分14分)
各项均为正数的数列{an}的前n项和Sn,函数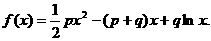
(其中p、q均为常数,且p>q>0),当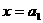 时,函数f(x)取得极小值,点
时,函数f(x)取得极小值,点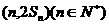 均在函数
均在函数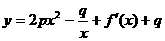 的图象上,(其中f′(x)是函数f(x)的导函数)
的图象上,(其中f′(x)是函数f(x)的导函数)
(1)求a1的值;
(2)求数列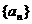 的通项公式;
的通项公式;
(3)记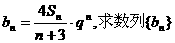 的前n项和Tn.
的前n项和Tn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com