
题目列表(包括答案和解析)
2、已知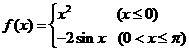 ,若
,若 ,则
,则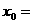 。
。
1、已知集合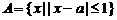 ,
,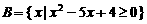 。若
。若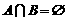 ,则实数
,则实数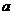 的取值范围是____________。
的取值范围是____________。
19. (12分)设某物体一天中的温度T是时间t的函数,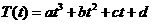 ,
,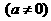 其中温度的单位是
其中温度的单位是 ,时间的单位是小时。t=0表示12:00, t取正值表示12:00点以后。若测得该物体在8:00的温度为8
,时间的单位是小时。t=0表示12:00, t取正值表示12:00点以后。若测得该物体在8:00的温度为8 ,12:00的温度为60
,12:00的温度为60 ,13:00的温度为58
,13:00的温度为58 ,且已知该物体的温度在8:00和16:00有相同的变化率。
,且已知该物体的温度在8:00和16:00有相同的变化率。
(1)写出该物体的温度T关于时间t的函数关系式;
(2)该物体在10:00到14:00这段时间中(包括10:00,14:00)何时温度最高?并求出最高温度。
(1)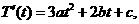 依题意得
依题意得
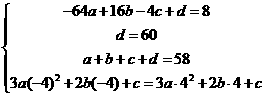
解得:a=1,b=0,c=-3,d=60 故T(t)=t3-3t+60
(2)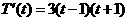 =0,得:
=0,得: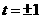
比较T(-2),T(-1),T(1),T(2)知,在10:00 14:00这段时间中,该物体在11:00和14:00的温度最高,且最高温度为62
14:00这段时间中,该物体在11:00和14:00的温度最高,且最高温度为62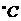 .
.
9、一条走廊宽 2 m, 长 8 m, 用 6 种颜色的 1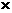 1 m
1 m 的整块地砖来铺设(每块地砖都是单色的, 每种颜色的地砖都足够多), 要求相邻的两块地砖颜色不同, 那么所有的不同拼色方法有
( D)
的整块地砖来铺设(每块地砖都是单色的, 每种颜色的地砖都足够多), 要求相邻的两块地砖颜色不同, 那么所有的不同拼色方法有
( D)
(A)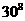 个 (B)
个 (B) 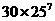 个 C.
个 C. 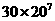 个 (D)
个 (D) 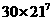 个
个
(18)已知等比数列{an}的前n项和为Sn.
(Ⅰ)若Sm,Sm+2,Sm+1成等差数列,证明am,am+2,am+1成等差数列;
(Ⅱ)写出(Ⅰ)的逆命题,判断它的真伪,并给出证明.
证 (Ⅰ) ∵Sm+1=Sm+am+1,Sm+2=Sm+am+1+am+2.
由已知2Sm+2=Sm+Sm+1,∴ 2(Sm+am+1+am+2)=Sm+(Sm+am+1),
∴am+2=-am+1,即数列{an}的公比q=-.
∴am+1=-am,am+2=am,∴2am+2=am+am+1,∴am,am+2,am+1成等差数列.
(Ⅱ) (Ⅰ)的逆命题是:若am,am+2,am+1成等差数列,则Sm,Sm+2,Sm+1成等差数列.
设数列{an}的公比为q,∵am+1=amq,am+2=amq2.
由题设,2am+2=am+am+1,即2amq2=am+amq,即2q2-q-1=0,∴q=1或q=-.
当q=1时,A≠0,∴Sm, Sm+2, Sm+1不成等差数列.
逆命题为假.
7.二元函数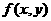 定义域为
定义域为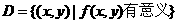 ,则函数
,则函数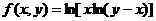 的定义域所表示的平面区域是(B)
的定义域所表示的平面区域是(B)
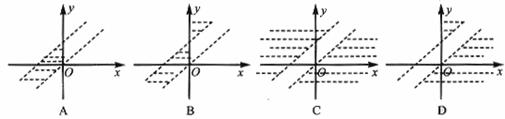
4、已知等差数列{an}的首项a1=120,d=-4,记Sn= a1+a2+…+an,若Sn≤an(n>1),则n最小值为………………………………………………………………………………(B )
(A)60 (B)62 (C)63 (D)70
15.在ABC中,若:= = ,则COSA等于_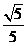 __________.
__________.
8、某班有48名学生,某次数学考试,算术平均分为70分,标准差为s,后来发现成绩记录有误,某甲得80分却误记为50分,某乙得70分却误记为100分,更正后计算得标准差为s1,则s1和s之间的大小关系为 …………………………………………………(D )
(A) s1>s (B) s1=s (C) s+5<s1 (D) s>s1
31.已知双曲线 的焦点分别为F1、F2,点P在双曲线上且|PF1|
=4|PF2|,则双曲线离心率的最大值为(
B )
的焦点分别为F1、F2,点P在双曲线上且|PF1|
=4|PF2|,则双曲线离心率的最大值为(
B )
A.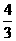 B.
B.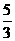 C.2 D.
C.2 D.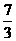
30、 如图,平面内的两条相交直线
如图,平面内的两条相交直线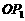 和
和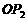 将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界). 若
将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界). 若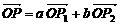 ,且点
,且点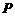 落在第Ⅲ部分,则实数
落在第Ⅲ部分,则实数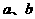 满足( B
)
满足( B
)
(A) 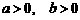 .
(B)
.
(B) 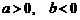 .
.
(C) 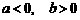 .
(D)
.
(D) 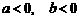 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com