
题目列表(包括答案和解析)
2.设全集为R,A={x|-1<x<1},B={ x| x≥0},则CR(A∪B)等于( )
A.{x|0≤x<1} B.{x| x≥0} C.{x|x≤-1} D.{x|x>-1}
1.复数i(1一i)等于( )
A.1+i B.1一i C.一1+i D.一1一i
20、(本小题满分16分)
椭圆G: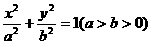 的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足
的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足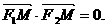
(Ⅰ)求离心率e的取值范围;
(Ⅱ)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为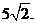
(1)求此时椭圆G的方程;
(2)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、
B,Q为AB的中点,问A、B两点能否关于过点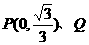 的直线对称?若能,求出k
的直线对称?若能,求出k
19、(本小题满分16分)
甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x)、g(x),当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险。
(Ⅰ)试解释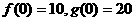 的实际意义;
的实际意义;
(Ⅱ)设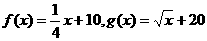 ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
18、(本小题满分16分)
设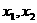 是函数
是函数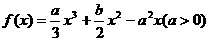 的两个极值点,且
的两个极值点,且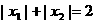
(Ⅰ)求a的取值范围;
(Ⅱ)求证: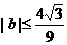 .
.
17、(本小题满分14分)
已知数列{an}的前n项和为Sn,且满足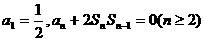
(Ⅰ)判断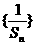 是否为等差数列?并证明你的结论;
是否为等差数列?并证明你的结论;
(Ⅱ)求Sn和an
|
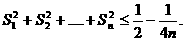
16、(本小题满分14分)已知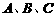 是
是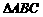 的三个内角,
的三个内角,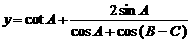 。
。
(1)若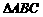 是正三角形,求
是正三角形,求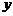 的值;
的值;
(2)若任意交换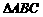 中两个角的位置,
中两个角的位置,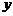 的值是否变化?证明你的结论;
的值是否变化?证明你的结论;
(3)若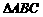 中有一内角为
中有一内角为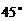 ,求
,求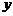 的最小值。
的最小值。
15、(本小题满分14分)
已知a、b、c是△ABC三边长,关于x的方程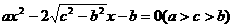 的两根之差的平方等于4,△ABC的面积
的两根之差的平方等于4,△ABC的面积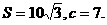
(Ⅰ)求角C;
(Ⅱ)求a、b的值.
14、符号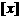 表示不超过
表示不超过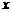 的最大整数,如
的最大整数,如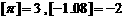 。定义函数
。定义函数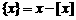 ,给出如下四个命题:①函数
,给出如下四个命题:①函数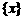 的定义域为
的定义域为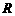 ,值域为
,值域为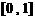 ; ②方程
; ②方程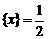 有无数解;
有无数解;
③函数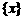 是周期函数;
④函数
是周期函数;
④函数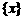 是
是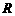 上的增函数。
上的增函数。
其中正确命题的序号是 。
13、如图,在矩形ABCD中,AB=1,BC=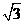 ,此矩形沿地面上一直线滚动,在滚动过程中始终与地面垂直,设直线BC与地面所成角为
,此矩形沿地面上一直线滚动,在滚动过程中始终与地面垂直,设直线BC与地面所成角为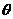 ,矩形周边上最高点离地面的距离为
,矩形周边上最高点离地面的距离为

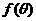 ,则
,则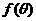 = 。
= 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com