
题目列表(包括答案和解析)
1 已知
已知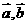 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么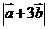 =
=
(A)4 (B)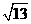 (C)
(C)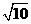 (D)
(D)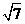
2 过点
过点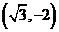 的直线
的直线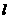 经过圆
经过圆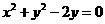 的圆心,则直线
的圆心,则直线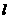 的倾斜角大小为
的倾斜角大小为
(A)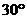 (B)
(B) (C)
(C) (D)
(D)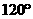
3 设函数f( x )的图象关于点(1,
设函数f( x )的图象关于点(1,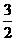 )对称,且存在反函数
)对称,且存在反函数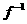 ( x ),若f(3) = 0,
( x ),若f(3) = 0,
则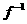 (3)等于
(3)等于
(A)-1 (B)1 (C)-2 (D)2
4 设m,n是两条不同的直线,α、β、γ是三个不同的平面
设m,n是两条不同的直线,α、β、γ是三个不同的平面 给出下列四个命题:
给出下列四个命题:
①若m⊥α,n∥α,则m⊥n; ②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n; ④若α∥β,β∥γ,m⊥α,,则m⊥γ
其中正确命题的序号是:
(A) ①和② (B)②和③ (C)③和④ (D)①和④
5.函数y = cos(2x+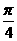 )的一条对称轴方程是
)的一条对称轴方程是
(A)x = -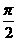 (B)x = -
(B)x = -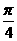 (C)x = -
(C)x = -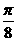 (D)x =
(D)x = 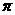
6
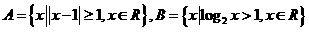 ,则“
,则“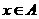 ”是“
”是“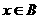 ”的
”的
(A)充分非必要条件 (B)必要非充分条件
(C)充分必要条件 (D)既非充分也非必要条件
 7
7 若点
若点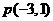 在双曲线
在双曲线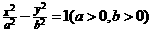 的左准线上,过点
的左准线上,过点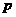 且方向向量为
且方向向量为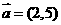 的光线,经直线
的光线,经直线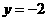 反射后通过双曲线的左焦点,则这个双曲线的离心率为( )
反射后通过双曲线的左焦点,则这个双曲线的离心率为( )
(A)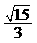 (B)
(B) (C)
(C)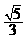 (D)
(D)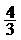
22.(14分)已知方向向量为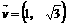 的直线
的直线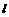 过椭圆C:
过椭圆C: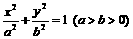 的焦点以及点(0,
的焦点以及点(0,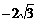 ),椭圆C的中心关于直线
),椭圆C的中心关于直线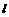 的对称点在椭圆C的右准线上。
的对称点在椭圆C的右准线上。
⑴求椭圆C的方程。
⑵是否存在过点E(-2,0)的直线 交椭圆C于点M、N,使⊿MON的面积为
交椭圆C于点M、N,使⊿MON的面积为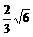 ,(O为坐标原点)?若存在,求出直线
,(O为坐标原点)?若存在,求出直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
21.(12分)已知二次函数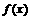 的二次项系数为
的二次项系数为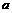 ,且不等式
,且不等式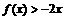 的解集为
的解集为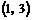

⑴若方程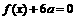 有两个相等的实数根,求
有两个相等的实数根,求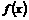 的解析式;
的解析式;
⑵若函数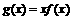 无极值,求实数
无极值,求实数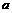 的取值范围
的取值范围
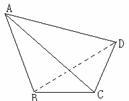
20.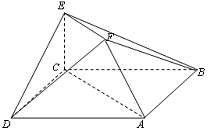 (12分)在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
(12分)在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=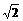 ,EF=EC=1,
,EF=EC=1,
⑴求证:平面BEF⊥平面DEF;
⑵求二面角A-BF-E的大小。
19.(12分)某汽车驾驶学校在学员结业前,对学员的驾驶技术进行4次考核,规定:学员必须按顺序从第一次开始参加考核,一旦考核合格就不必参加以后的考核,否则还需参加下次考核。若学员小李参加每次考核合格的概率依次组成一个公差为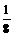 的等差数列,他参加第一次考核合格的概率不超过
的等差数列,他参加第一次考核合格的概率不超过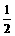 ,且他直到参加第二次考核才合格的概率为
,且他直到参加第二次考核才合格的概率为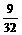 。
。
⑴求小李第一次参加考核就合格的概率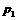 ;
;
⑵求小李第四次参加考核的概率。
18.(12分)已知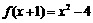 ,等差数列
,等差数列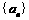 中,
中,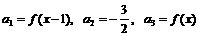 ;
;
⑴求实数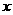 的值;
的值;
⑵求数列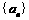 的通项公式;
的通项公式;
⑶求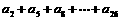 的值;
的值;
17.(12分)已知函数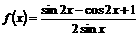 .
.
⑴求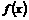 的定义域;
的定义域;
⑵设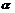 为任意角,且
为任意角,且 ,求
,求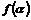 的值。
的值。
16.设函数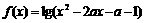 ,给出如下命题:
,给出如下命题:
①无论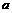 取何实数,函数
取何实数,函数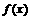 的值域都是R;②函数
的值域都是R;②函数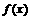 必有最小值;③若
必有最小值;③若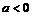 ,且
,且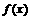 的定义域为
的定义域为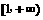 ,则函数
,则函数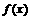 有反函数;④对于任意实数
有反函数;④对于任意实数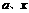 ,一定有
,一定有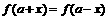 ,
,
其中正确命题的序号是 。(将你认为正确的命题的序号都填上)
草 稿 纸
-----------------------------------------------------------------------------------
15.如图,正方形ABCD中,E、F分别是AB、AD的中点,将此正方形沿
EF折成直二面角后,异面直线AF与BE所成角的余弦值为 .
14.在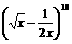 展开式中,含
展开式中,含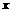 的负整数指数幂的项共有 项.
的负整数指数幂的项共有 项.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com