
题目列表(包括答案和解析)
2.当x ³ a 时, 不等式化成: 2x –x + a > 2, 得 x > 2 – a , 2分
由a =2 – a,得a = 1 1分
1) 当 a £ 1时, ∵a <2 – a , ∴x > 2 – a,
2) 当a > 1时, ∵a >2 – a, ∴ x ³ a. 3分
综合上述: 当 a £ 1时, 原不等式解为 x >2 – a ,
当a >1时, 原不等式解为 x > 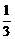 ( a + 2)
2分
( a + 2)
2分
其它解法: 1 ) 2x – 2 > | x – a | 平方求解.
2) 图象法
对照上面给分.
1.当x < a时, 不等式化成: 2x + x– a > 2, 得 x > 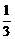 ( a + 2),
2分
( a + 2),
2分
a = 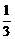 ( a + 2), 得a = 1 1分
( a + 2), 得a = 1 1分
1) 当 a £ 1时, ∵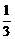 ( a + 2) ≥ a , ∴ 无解 ,
( a + 2) ≥ a , ∴ 无解 ,
2) 当 a >1时, ∵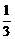 ( a + 2) < a, ∴解为
( a + 2) < a, ∴解为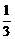 ( a + 2)< x < a .
3分
( a + 2)< x < a .
3分
19. (本小题满分14分)
18. (本小题满分14分)
(1) ∵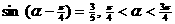 , ∴
, ∴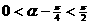 , 有
, 有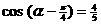 ; --- 4分
; --- 4分
(2) 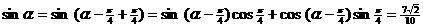 ;
--- 5分
;
--- 5分
(3) 函数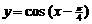 的图象可以通过函数
的图象可以通过函数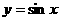 的图象向左平移
的图象向左平移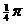 个单位得到.
---
5分
个单位得到.
---
5分
17. 2(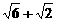 )k
.
)k
.
15. p 16. (–¥, – 1]∪[1,¥)
13. – 1 14. 1215 .
11. [0,¥) 12. 4 .
22.(本小题满分16分)
已知数列{bn}满足条件: 首项b1
= 1, 前n项之和Bn = 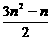 .
.
(1) 求数列{bn}的通项公式 ;
(2) 设数列{an}的满足条件:an= (1+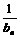 ) a n – 1 ,且a1 = 2 , 试比较an与
) a n – 1 ,且a1 = 2 , 试比较an与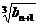 的大小,并证明你的结论.
的大小,并证明你的结论.
数学参考评分标准(理科)
21. (本小题满分14分)
已知向量x = (1,t2 – 3 ) , y = (–k ,t) (其中实数k和t不同时为零),当| t | £ 2时, 有 x⊥y ,当| t | > 2时,有x∥y.
(1) 求函数关系式k = f (t ) ;
(2) 求函数f (t )的单调递减区间;
(3) 求函数f (t )的最大值和最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com