
题目列表(包括答案和解析)
3.(人教A版必修2 第124页A组第3题)
求直线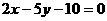 与坐标轴围成的三角形的面积.
与坐标轴围成的三角形的面积.
变式1:过点(-5,-4)且与两坐标轴围成的三角形面积为5的直线方程是 .
解:设所求直线方程为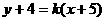 ,依题意有
,依题意有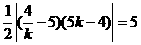 ,
,
∴ (无解)或
(无解)或 ,解得
,解得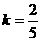 或
或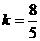 .
.
∴直线的方程是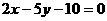 或
或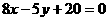 .
.
变式2:(2006年上海春季卷)已知直线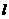 过点
过点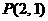 ,且与
,且与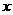 轴、
轴、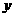 轴的正半轴分别交于
轴的正半轴分别交于 、
、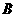 两点,
两点, 为坐标原点,则△OAB面积的最小值为 .
为坐标原点,则△OAB面积的最小值为 .
解:设直线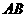 的方程为
的方程为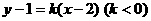 ,
,
则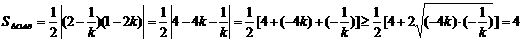 ,当且仅当
,当且仅当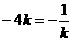 即
即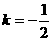 时取等号,∴当
时取等号,∴当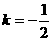 时,
时,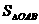 有最小值4.
有最小值4.
变式3:已知射线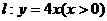 和点
和点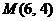 ,在射线
,在射线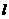 上求一点
上求一点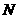 ,使直线
,使直线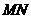 与
与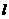 及
及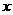 轴围成的三角形面积
轴围成的三角形面积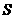 最小.
最小.
解:设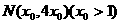 ,则直线
,则直线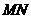 的方程为
的方程为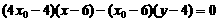 .令
.令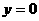 得
得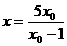 ,∴
,∴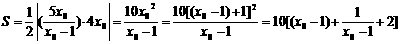
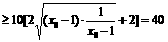 ,当且仅当
,当且仅当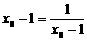 即
即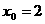 时取等号,∴当
时取等号,∴当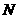 为(2,8)时,三角形面积
为(2,8)时,三角形面积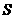 最小.
最小.
2.(人教A版必修2 第111页A组第9题)
求过点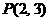 ,并且在两轴上的截距相等的直线方程.
,并且在两轴上的截距相等的直线方程.
变式1:直线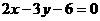 在
在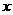 轴上的截距为
轴上的截距为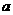 ,在
,在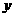 轴上的截距为
轴上的截距为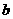 ,则( )
,则( )
A.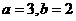 B.
B.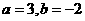 C.
C.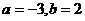 D.
D.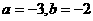
解:令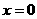 得
得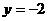 ,∴直线在
,∴直线在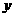 轴上的截距为
轴上的截距为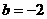 ;令
;令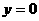 得
得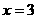 ,∴直线在
,∴直线在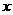 轴上的截距为
轴上的截距为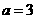 ,故选(B).
,故选(B).
变式2:过点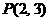 ,且在两坐标轴上的截距互为相反数的直线方程是 .
,且在两坐标轴上的截距互为相反数的直线方程是 .
解:依题意,直线的斜率为1或直线经过原点,∴直线的方程为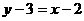 或
或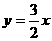 ,即
,即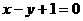 或
或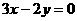 .
.
变式3:直线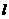 经过点
经过点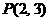 ,且与两坐标轴围成一个等腰直角三角形,求直线
,且与两坐标轴围成一个等腰直角三角形,求直线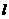 的方程.
的方程.
解:依题意,直线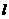 的斜率为±1,∴直线
的斜率为±1,∴直线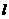 的方程为
的方程为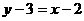 或
或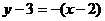 ,即
,即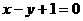 或
或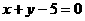 .
.
1.(北师大版必修2 第93 页A组第1题)
已知点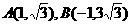 ,求直线
,求直线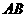 的斜率.
的斜率.
变式1:已知点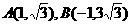 ,则直线
,则直线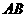 的倾斜角是( )
的倾斜角是( )
A.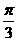 B.
B.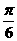 C.
C.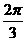 D.
D.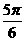
解:∵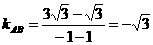 ,∴
,∴ ,∵
,∵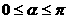 ,∴
,∴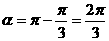 ,故选(C).
,故选(C).
变式2:(2006年北京卷)若三点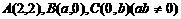 共线,则
共线,则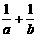 的值等于 .
的值等于 .
解:∵ 、
、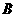 、
、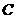 三点共线,∴
三点共线,∴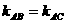 ,∴
,∴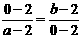 ,∴
,∴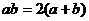 ,∴
,∴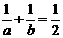 .
.
变式3:已知点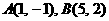 ,直线
,直线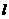 的倾斜角是直线
的倾斜角是直线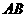 的倾斜角的一半,求直线
的倾斜角的一半,求直线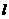 的斜率.
的斜率.
解:设直线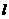 的倾斜角为
的倾斜角为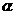 ,则直线
,则直线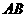 的倾斜角为
的倾斜角为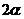 ,依题意有
,依题意有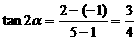 ,∴
,∴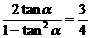 ,∴
,∴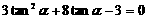 ,∴
,∴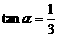 或
或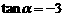 .由
.由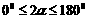 ,得
,得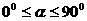 ,∴
,∴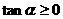 ,∴
,∴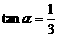 ,∴直线
,∴直线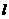 的斜率为
的斜率为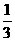 .
.
8.(★★★★★)已知双曲线C的两条渐近线都过原点,且都以点A(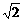 ,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
(1)求双曲线C的方程.
(2)设直线l过点A,斜率为k,当0<k<1时,双曲线C的上支上有且仅有一点B到直线l的距离为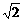 ,试求k的值及此时B点的坐标.
,试求k的值及此时B点的坐标.
7.(★★★★★)已知中心在原点,顶点A1、A2在x轴上,离心率e=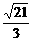 的双曲线过点P(6,6).
的双曲线过点P(6,6).
(1)求双曲线方程.
(2)动直线l经过△A1PA2的重心G,与双曲线交于不同的两点M、N,问:是否存在直线l,使G平分线段MN,证明你的结论.
6.(★★★★★)已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,且|AB|≤2p.
(1)求a的取值范围.
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
5.(★★★★★)在抛物线y2=16x内,通过点(2,1)且在此点被平分的弦所在直线的方程是_________.
4.(★★★★★)正方形ABCD的边AB在直线y=x+4上,C、D两点在抛物线y2=x上,则正方形ABCD的面积为_________.
3.(★★★★)已知两点M(1,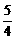 )、N(-4,-
)、N(-4,-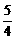 ),给出下列曲线方程:①4x+2y-1=0,
),给出下列曲线方程:①4x+2y-1=0,
②x2+y2=3,③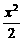 +y2=1,④
+y2=1,④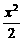 -y2=1,在曲线上存在点P满足|MP|=|NP|的所有曲线方程是_________.
-y2=1,在曲线上存在点P满足|MP|=|NP|的所有曲线方程是_________.
2.(★★★★)抛物线y=ax2与直线y=kx+b(k≠0)交于A、B两点,且此两点的横坐标分别为x1,x2,直线与x轴交点的横坐标是x3,则恒有( )
A.x3=x1+x2 B.x1x2=x1x3+x2x3
C.x1+x2+x3=0 D.x1x2+x2x3+x3x1=0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com