
题目列表(包括答案和解析)
5.代数式 的展开式中,含
的展开式中,含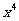 项的系数是
项的系数是
A.-30 B.30 C.70 D.90
4.数列{an}满足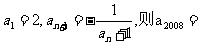
A.2 B.-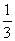 C.-
C.-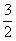 D.1
D.1
3.函数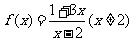 的反函数
的反函数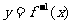 的一个单调减区间是
的一个单调减区间是
A.(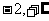 ) B.(
) B.(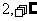 ) C.(
) C.(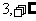 ) D.(
) D.(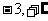 )
)
2.已知集合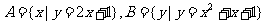 ,则
,则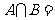
A.{(0,1),(1,3)} B.R
C.(0,+∞) D.[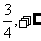 )
)
1.直线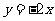 按向量
按向量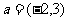 的平移后,得到的直线方程为
的平移后,得到的直线方程为
A.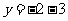 B.
B.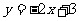
C.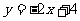 D.
D.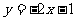
4.有意识地与解析几何(特别是切线、最值)、函数的单调性、函数的极值、最值、二次函数、方程、不等式等进行交汇,综合运用。特别是精选一些以导数为工具分析和解决一些函数问题,以及一些实际问题中的最大(小)值问题。
3.题目的难度要控制好,不要太难,应以方法的本质为主。
2.对极限和导数的概念以及导数的实际背景一定要深入了解。
1.极限内容和简单的函数求导在高考中以填空题和解答题为主。考生应立足基础只是和基本方法的复习,以课本题目为主,以熟练技能,巩固概念为目标。
22. (Ⅰ) 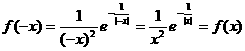
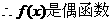 。
。
(Ⅱ)当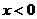 时,
时,
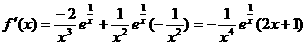
令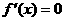 有
有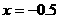 ,
,
当x变化时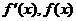 的变化情况如下表: 由表可知:
的变化情况如下表: 由表可知:
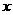 |
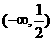 |
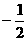 |
(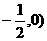 |
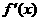 |
+ |
0 |
- |
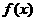 |
增 |
极大值 |
减 |
当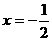 时
时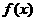 取极大值
取极大值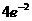 .
.
(Ⅲ)当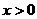 时
时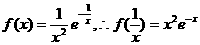
考虑到: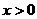 时,不等式
时,不等式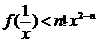 等价于
等价于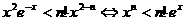 …(1)
…(1)
所以只要用数学归纳法证明不等式(1)对一切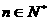 都成立即可
都成立即可
(i)当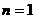 时,设
时,设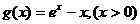
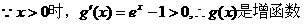 ,
,
故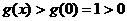 ,即
,即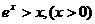
所以,当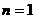 时,不等式(1)都成立
时,不等式(1)都成立
(ii)假设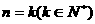 时,不等式(1)都成立,即
时,不等式(1)都成立,即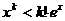
当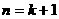 时设
时设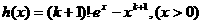
有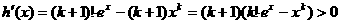
故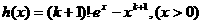 为增函数,
为增函数,
所以,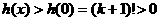 ,即
,即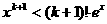 ,
,
这说明当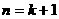 时不等式(1)也都成立,
时不等式(1)也都成立,
根据(i)(ii)可知不等式(1)对一切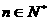 都成立,
都成立,
故原不等式对一切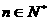 都成立.
都成立.
6 复习建议
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com