
题目列表(包括答案和解析)
4、极坐标方程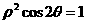 表示的曲线为
表示的曲线为
A、两条直线 B、椭圆 C、双曲线 D、抛物线
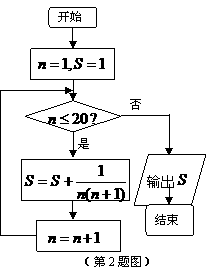
3、一个几何体的三视图如上图所示,则该几何体外接球的表面积为
A、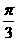 B、
B、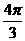 C、
C、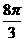 D、
D、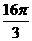
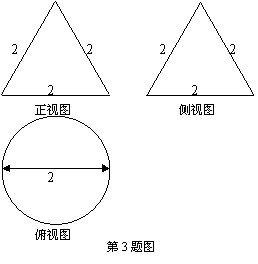
2、下面框图表示的程序所输出的结果是
 A、
A、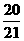 B、
B、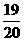 C、
C、 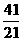 D、
D、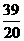
1、
复数z满足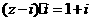 ,则复数z的模为
,则复数z的模为
A、2
B、1 C、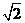 D、
D、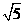
22、(1)设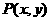 ,
,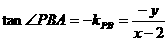 ,
,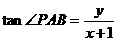
∵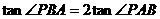
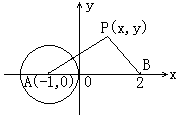 ∴
∴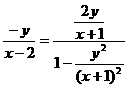 ,
,
∴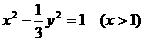 (4分)
(4分)
(2)设PE斜率为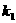 ,PR斜率为
,PR斜率为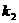
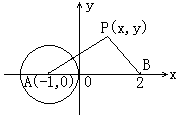 PE:
PE: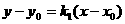 PR:
PR: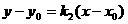
令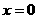 ,
,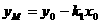 ,
,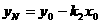
∴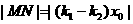 ……(2分)
……(2分)
由PF和园相切得: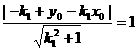 ,PR和园相切得:
,PR和园相切得: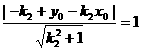
故: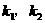 为
为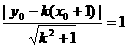 两解
两解
故有: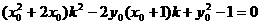
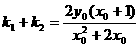 ,
,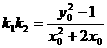 (2分)
(2分)
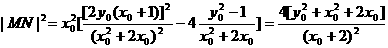
又∵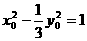 ,∴
,∴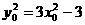 ,∴
,∴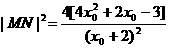 (3分)
(3分)
设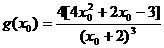 ,
,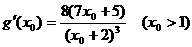
故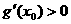
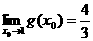 ,
,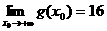
∴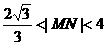 (3分)
(3分)
本资料由《七彩教育网》 提供!
21、(1)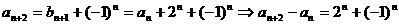
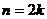 时,
时,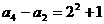
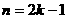 时,
时,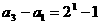
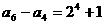
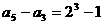
…… ……
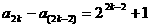
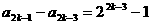
∴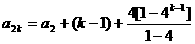 ∴
∴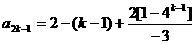
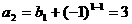
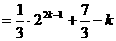
∴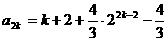 ∴
∴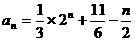 (3分)
(3分)
∴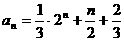 (3分)
(3分)
(2)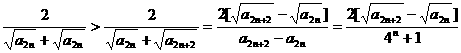
又∵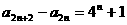 ,∴
,∴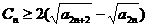
∴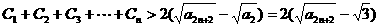 (6分)
(6分)
20、方法1:
(1)过S作 ,
,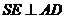 ,连
,连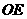
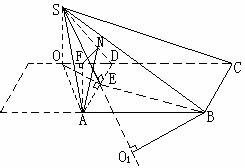 ∴
∴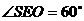
∴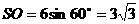 ……4分
……4分
(2)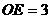 ,
,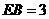 ,∴
,∴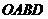 是平行四边形
是平行四边形
故平面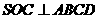
过A作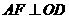 ,
,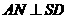 ,连
,连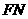
∴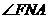 为平面
为平面 和
和
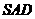 二面角平面角,而
二面角平面角,而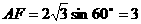
应用等面积: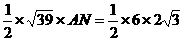 ,
,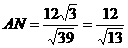
∵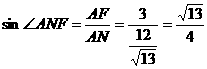 ,
,
故题中二面角为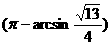 ……4分
……4分
(3)∵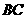 ∥
∥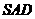 ,
,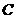 到
到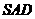 距离为
距离为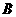 到
到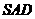 距离
距离
又∵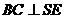 ,
,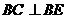 ,∴
,∴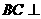 平面
平面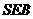 ,∴
,∴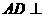 平面
平面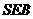
∴平面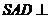 平面
平面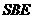 ,只需B作SE垂直BO1,BO1=
,只需B作SE垂直BO1,BO1=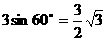
设线面角为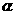 ,
,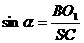 ,
,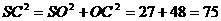 ,
,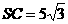
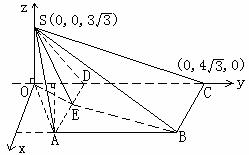 ∴
∴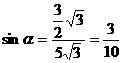 ,故线面角为
,故线面角为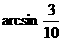 ……4分
……4分
方法2:
(1)同上
(2)建立直角坐标系
平面SDC法向量为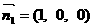 ,
,
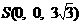 ,
, ,
,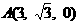
设平面SAD法向量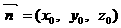
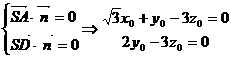 ,取
,取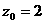 ,
,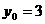 ,
,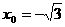
∴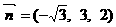 ∴
∴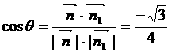
∴二面角为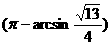
(3)设线面角为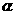 ,
,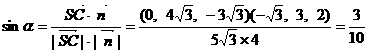
∴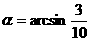
19、(1)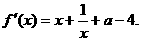

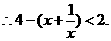 所以
所以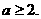
(2)设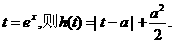
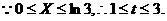 ……8分
……8分
当 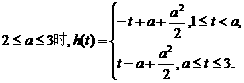

当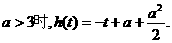

所以,当
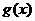 的最小值为
的最小值为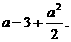 ………………………………
12分
………………………………
12分
18、(1)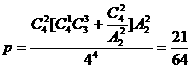 ……5分
……5分
(2)分布列:
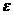 |
0 |
1 |
2 |
3 |
4 |
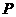 |
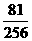 |
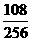 |
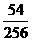 |
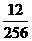 |
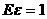 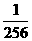 |
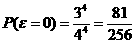 ,
,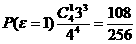 ,
,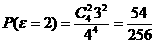
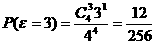 ,
,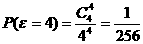
评分:下面5个式子各1分,列表和期望计算2分(5+2=7分)
17、(1)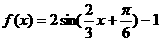 ……2分
……2分
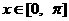
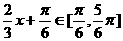
∴当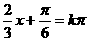 ∴
∴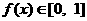 ……4分
……4分
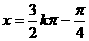 ,对称中心
,对称中心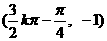
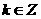 ……6分
……6分
(2)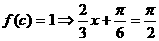
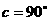 ……8分
……8分
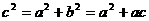 ……10分
……10分
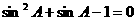 ,
,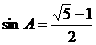 ……12分
……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com