
题目列表(包括答案和解析)
2.某校高三(1)班有48名学生,高三(2)班有42名学生,现要用分层抽样的方法从中抽取一个容量为15的样本,则需要从高三(1)班抽取的学生人数为
A.6 B.7 C.8 D.10
1.已知全集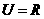 ,集合
,集合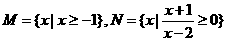 ,则
,则
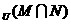
A.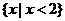 B.
B.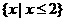
C.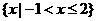 D.
D.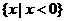
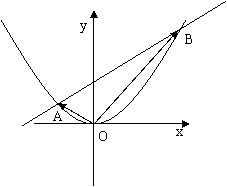
22、如图,过抛物线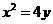 的对称轴上一点P(0,b ) (b>0)作直线与抛物线交于A、B两点,
的对称轴上一点P(0,b ) (b>0)作直线与抛物线交于A、B两点,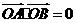 。
。
(1)求b的值;
(2)设以A、B 为切点的抛物线的切线交于点M ,起点M的轨迹方程;
 (3)是否存在直线y
(3)是否存在直线y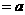 ,被以AB为直径的圆截得的弦长为定值,如果存在,请求出此直线的方程;如果不存在,说明理由。
,被以AB为直径的圆截得的弦长为定值,如果存在,请求出此直线的方程;如果不存在,说明理由。
本资料由《七彩教育网》 提供!
21、已知数列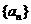 的前n项和
的前n项和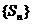 满足
满足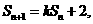 又
又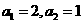
(1)求k的值;
(2)求数列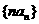 的前n项和
的前n项和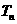 ;
;
(3)是否存在整数m、n,使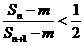 成立?若存在,求出这样的正整数;若不存在,说明理由。
成立?若存在,求出这样的正整数;若不存在,说明理由。
20、设函数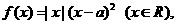 其中
其中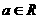 。
。
(1)当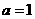 时,求曲线
时,求曲线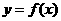 在点(2,f(2))处的切线方程;
在点(2,f(2))处的切线方程;
(2)当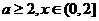 时,函数
时,函数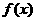 的最大值为8,求
的最大值为8,求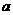 ;
;
(3)当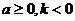 时,
时,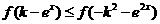 对任意的
对任意的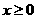 恒成立,求k的取值范围。
恒成立,求k的取值范围。
19、甲盒中有6个红球,4个白球;乙盒中有4个红球,4个白球,这些球除颜色外完全相同。
(1)从甲盒中任取3个球,求取出红球的个数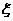 的分布列与期望;
的分布列与期望;
(2)若从甲盒中任取2个球放入乙盒中,然后再从乙盒中任取一个球,求取出的这个球是白球的概率。
18、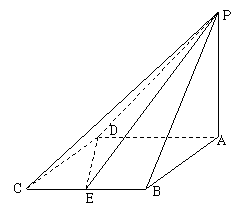 如图四棱锥P-ABCD 的底面是边长为2的菱形,且
如图四棱锥P-ABCD 的底面是边长为2的菱形,且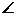 BAD=600,PA⊥平面ABCD,设E为BC的中点,二面角P-DE-A为
BAD=600,PA⊥平面ABCD,设E为BC的中点,二面角P-DE-A为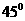
(1)在PA上确定一点F,使BF//平面PDE;
 (2)求平面PDE与平面PAB所成的锐二面角的正切值。
(2)求平面PDE与平面PAB所成的锐二面角的正切值。
17、在△ABC中,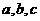 分别为角A、B、C所对的三边,
分别为角A、B、C所对的三边,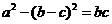 ,
,
(Ⅰ)求角A;
(Ⅱ)若BC=2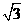 ,角B等于x周长为y,求函数
,角B等于x周长为y,求函数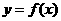 的取值范围。
的取值范围。
16、给出下列四个结论:
①合情推理是由特殊到一般的推理,得到的结论不一定正确,演绎推理是由一般到特殊的推理,得到的结论一定正确;
②一般地,当r的绝对值大于0.75时,认为两个变量之间有很强的线性相关关系。如果变量y与x之间的相关系数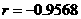 ,则变量y与x之间具有线性关系;
,则变量y与x之间具有线性关系;
③用独立性检验(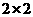 列联表法)来考察两个分类变量是否有关系时,算出的随机变量
列联表法)来考察两个分类变量是否有关系时,算出的随机变量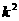 的值越大,说明“X 与Y有关系”成立的可能性越大;
的值越大,说明“X 与Y有关系”成立的可能性越大;
④命题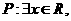 使得
使得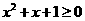 ,则
,则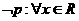 均有
均有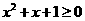 。
。
其中结论正确的序号为_____________________ .(请写出你认为正确的所有结论的序号)
15、若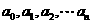 成等差数列,则有等式
成等差数列,则有等式 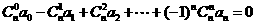 成立,类比上述性质,相应地:若
成立,类比上述性质,相应地:若
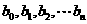 成等比数列,则有等式_________成立。
成等比数列,则有等式_________成立。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com