
题目列表(包括答案和解析)
1、设全集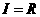 ,集合
,集合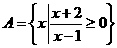 ,则
,则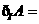 ______________。
______________。
21.(本题满分20分,第1小题4分,第2 小题6分,第三小题10分)
已知数列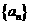 中,
中,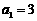 ,
,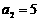 ,其前
,其前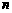 项和
项和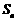 满足
满足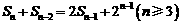 .令
.令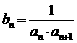 .
.
(1)求数列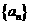 的通项公式;
的通项公式;
(2)若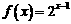 ,求证:
,求证: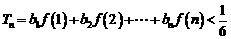 (
(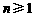 );
);
(3)令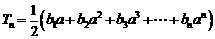 (
(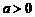 ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有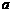 的值:①对于任意正整数
的值:①对于任意正整数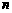 ,都有
,都有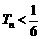 ;②对于任意的
;②对于任意的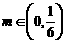 ,均存在
,均存在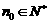 ,使得
,使得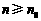 时,
时,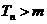 .
.
20.(本小题满分16分,第1小题4分,第2小题6分,第3小题6分)
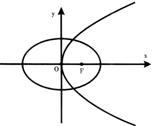
设椭圆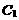 的中心在原点,其右焦点与抛物线
的中心在原点,其右焦点与抛物线 :
: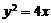 的焦点F重合,过点F与x轴垂直的直线与
的焦点F重合,过点F与x轴垂直的直线与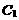 交于A、B两点,与
交于A、B两点,与 交于C、D两点,已知
交于C、D两点,已知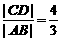 。
。
(1)过点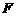 且倾斜角为
且倾斜角为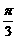 的直线与
的直线与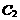 :
: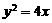 交于
交于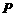 、
、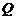 两点,求
两点,求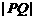 的值;
的值;
(2)求椭圆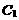 的方程;
的方程;
(3)过点F的直线l与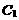 交于M、N两点,与
交于M、N两点,与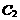 交于P、Q两点, 若
交于P、Q两点, 若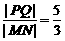 ,求直线l的方程。
,求直线l的方程。
19.(本题满分14分,第1小题7分,第2小题7分)
已知:某型号进口仪器每台降价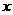 成(1成为
成(1成为 ),那么售出数量就增加
),那么售出数量就增加 成(
成(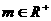 常数)
常数)
(1)当某商场现在定价为每台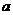 元,售出
元,售出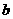 台,试建立降价后的营业额
台,试建立降价后的营业额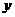 与每台降价
与每台降价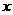 成的函数关系式,并求出
成的函数关系式,并求出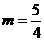 时,每台降价多少成时,营业额
时,每台降价多少成时,营业额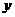 最大?
最大?
(2)为使营业额增加,求 的取值范围。
的取值范围。
|
18.(本题满分12分,第1小题6分,第2 小题6分)
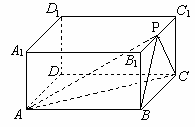
在正四棱柱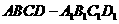 中,
中,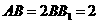 ,P为B1C1的中点.
,P为B1C1的中点.
(1)求直线AP与平面B1BCC1所成的角;
(2)求点P到平面CDB1的距离。
17.(本题满分12分,第1小题6分,第2 小题6分)
已知函数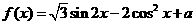 (
(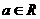 ,
,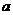 为常数),
为常数),
(1)求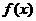 的周期和单调递增区间;
的周期和单调递增区间;
(2)若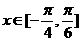 时,
时,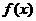 的最小值为4,求
的最小值为4,求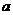 的值。
的值。
16.定义区间长度 为这样的一个量:
为这样的一个量: 的大小为区间右端点的值减去左端点的值.若关于
的大小为区间右端点的值减去左端点的值.若关于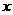 的不等式
的不等式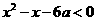 有解,且解集的区间长度不超过
有解,且解集的区间长度不超过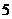 个单位长,则
个单位长,则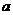 的取值范围是 ( )
的取值范围是 ( )
A.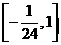 . B.
. B. .
.
C.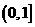 . D.
. D.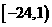 .
.
15.记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有 ( )种 ( )
A.1440种 B.960种 C.720种 D.480种
14.若函数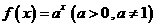 为增函数,那么
为增函数,那么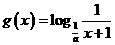 的图像是 ( )
的图像是 ( )
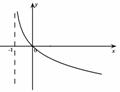
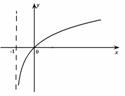
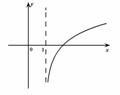
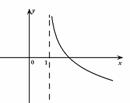
(A) (B) (C) (D)
13.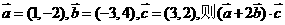 =
( )
=
( )
A.(-15,12) B.0 C. -3 D.-11
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com