
题目列表(包括答案和解析)
12. [答案]5
[答案]5
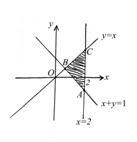
[解析]依题意,画出可行域(如图示),
则对于目标函数y=2x-z,
当直线经过A(2,-1)时,
z取到最大值,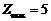 .
.
(2010湖北理数)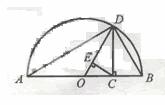 15.设a>0,b>0,称
15.设a>0,b>0,称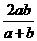 为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
3. (2010湖北理数)12.已知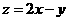 ,式中变量
,式中变量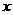 ,
,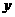 满足约束条件
满足约束条件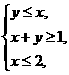 ,则
,则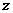 的最大值为___________.
的最大值为___________.
13. 4
[解析]不等式表示的区域是一个四边形,4个顶点是
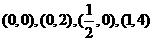 ,易见目标函数在
,易见目标函数在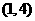 取最大值8,
取最大值8,
所以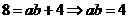 ,所以
,所以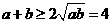 ,在
,在 时是等号成立。所以
时是等号成立。所以 的最小值为4.
的最小值为4.
[规律总结]线性规划问题首先作出可行域,若为封闭区域(即几条直线围成的区域)则区域端点的值是目标函数取得最大或最小值,求出直线交点坐标代入得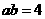 ,要想求
,要想求 的最小值,显然要利用基本不等式.
的最小值,显然要利用基本不等式.
2. (2010安徽理数)13、设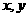 满足约束条件
满足约束条件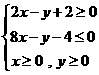 ,若目标函数
,若目标函数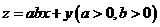 的最大值为8,则
的最大值为8,则 的最小值为________。
的最小值为________。
1. (2010安徽理数)

12.(2010湖北文数)已知: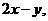 式中变量
式中变量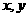 满足的束条件
满足的束条件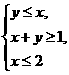 则z的最大值为______。
则z的最大值为______。
[答案]5
[解析]同理科
(2010山东理数)

15.①,③,⑤
[解析]令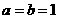 ,排除②②;由
,排除②②;由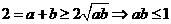 ,命题①正确;
,命题①正确;
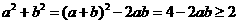 ,命题③正确;
,命题③正确;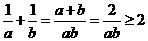 ,命题⑤正确。
,命题⑤正确。
(2010浙江文数)(15)若正实数X,Y 满足2X+Y+6=XY , 则XY 的最小值是 。
答案:18
(2010山东文数)(14)已知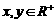 ,且满足
,且满足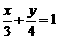 ,则xy的最大值为
.
,则xy的最大值为
.
答案:3
(2010北京文数)(11)若点p(m,3)到直线 的距离为4,且点p在不等式
的距离为4,且点p在不等式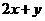 <3表示的平面区域内,则m=
。
<3表示的平面区域内,则m=
。
答案:-3
(2010全国卷1文数)(13)不等式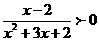 的解集是
.
的解集是
.
13.
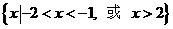 [命题意图]本小题主要考查不等式及其解法
[命题意图]本小题主要考查不等式及其解法
[解析]: 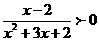
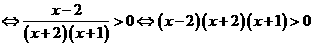 ,数轴标根得:
,数轴标根得: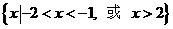
(2010全国卷1理数)(13)不等式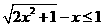 的解集是
.
的解集是
.

2.(2010上海文数)不等式 的解集是
的解集是 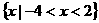 。
。
解析:考查分式不等式的解法 等价于(x-2)(x+4)<0,所以-4<x<2
等价于(x-2)(x+4)<0,所以-4<x<2
 (2010陕西文数)14.设x,y满足约束条件
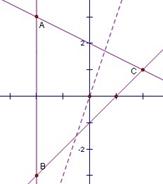
(2010陕西文数)14.设x,y满足约束条件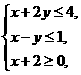 ,则目标函数z=3x-y的最大值为 5 .
,则目标函数z=3x-y的最大值为 5 .
解析:不等式组表示的平面区域如图所示,
当直线z=3x-y过点C(2,1)时,在y轴上截距最小
此时z取得最大值5
(2010辽宁文数)(15)已知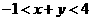 且
且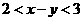 ,则
,则 的取值范围是
.
的取值范围是
.
(答案用区间表示)
解析:填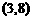 . 利用线性规划,画出不等式组
. 利用线性规划,画出不等式组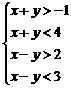 表示的平面区域,即可求解.
表示的平面区域,即可求解.
(2010辽宁理数)(14)已知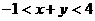 且
且 ,则
,则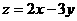 的取值范围是_______(答案用区间表示)
的取值范围是_______(答案用区间表示)
[答案](3,8)
[命题立意]本题考查了线性规划的最值问题,考查了同学们数形结合解决问题的能力。
[解析]画出不等式组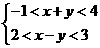 表示的可行域,在可行域内平移直线z=2x-3y,当直线经过x-y=2与x+y=4的交点A(3,1)时,目标函数有最小值z=2×3-3×1=3;当直线经过x+y=-1与x-y=3的焦点A(1,-2)时,目标函数有最大值z=2×1+3×2=8.
表示的可行域,在可行域内平移直线z=2x-3y,当直线经过x-y=2与x+y=4的交点A(3,1)时,目标函数有最小值z=2×3-3×1=3;当直线经过x+y=-1与x-y=3的焦点A(1,-2)时,目标函数有最大值z=2×1+3×2=8.
(2010安徽文数)(15)若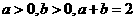 ,则下列不等式对一切满足条件的
,则下列不等式对一切满足条件的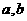 恒成立的是 (写出所有正确命题的编号).
恒成立的是 (写出所有正确命题的编号).
①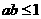 ; ②
; ②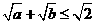 ; ③
; ③ 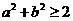 ;
;
④ ; ⑤
; ⑤
8.(2010福建理数)设不等式组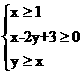 所表示的平面区域是
所表示的平面区域是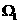 ,平面区域是
,平面区域是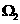 与
与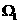 关于直线
关于直线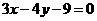 对称,对于
对称,对于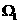 中的任意一点A与
中的任意一点A与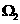 中的任意一点B,
中的任意一点B, 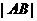 的最小值等于( )
的最小值等于( )
A.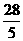 B.4 C.
B.4 C.
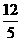 D.2
D.2
[答案]B
[解析]由题意知,所求的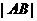 的最小值,即为区域
的最小值,即为区域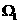 中的点到直线
中的点到直线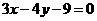 的距离的最小值的两倍,画出已知不等式表示的平面区域,如图所示,
的距离的最小值的两倍,画出已知不等式表示的平面区域,如图所示,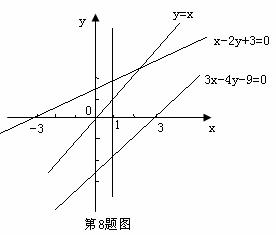
可看出点(1,1)到直线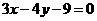 的距离最小,故
的距离最小,故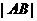 的最小值为
的最小值为
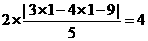 ,所以选B。
,所以选B。
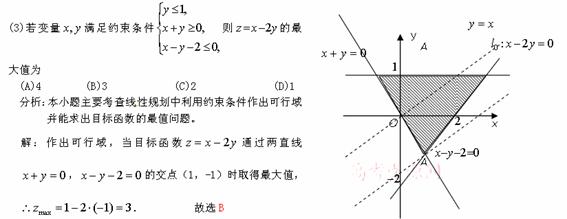
3.B [命题意图]本小题主要考查线性规划知识、作图、识图能力及计算能力.
 [解析]画出可行域(如右图),
[解析]画出可行域(如右图),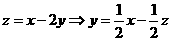 ,由图可知,当直线
,由图可知,当直线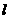 经过点A(1,-1)时,z最大,且最大值为
经过点A(1,-1)时,z最大,且最大值为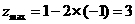 .
.

(2010全国卷1理数)(8)设a=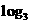 2,b=ln2,c=
2,b=ln2,c=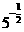 ,则
,则
(A) a<b<c (B)b<c<a (C) c<a<b (D) c<b<a

(2010全国卷1理数)
(2010四川文数)(11)设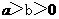 ,则
,则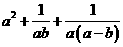 的最小值是
的最小值是
(A)1 (B)2 (C)3 (D)4
解析: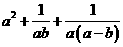
=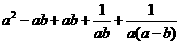
=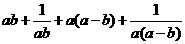
≥2+2=4
当且仅当ab=1,a(a-b)=1时等号成立
如取a=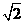 ,b=
,b=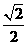 满足条件.
满足条件.
答案:D
(2010四川文数) (8)某加工厂用某原料由车间加工出
(8)某加工厂用某原料由车间加工出 产品,由乙车间加工出
产品,由乙车间加工出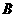 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克
产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克 产品,每千克
产品,每千克 产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克
产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克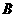 产品,每千克
产品,每千克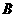 产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为
产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为
(A)甲车间加工原料10箱,乙车间加工原料60箱
(B)甲车间加工原料15箱,乙车间加工原料55箱
(C)甲车间加工原料18箱,乙车间加工原料50箱
(D)甲车间加工原料40箱,乙车间加工原料30箱
解析:解析:设甲车间加工原料x箱,乙车间加工原料y箱
则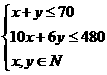
目标函数z=280x+300y
结合图象可得:当x=15,y=55时z最大
本题也可以将答案逐项代入检验.
答案:B
(2010山东理数)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com