
题目列表(包括答案和解析)
(13) 的展开式中的第四项是
. w_w_w.k*s 5*
的展开式中的第四项是
. w_w_w.k*s 5*
解析:T4=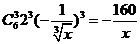 w_w_w.k*s 5*
w_w_w.k*s 5*
答案:-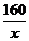
(14)直线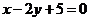 与圆
与圆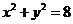 相交于A、B两点,则
相交于A、B两点,则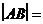 .
.
解析:方法一、圆心为(0,0),半径为2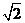
圆心到直线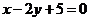 的距离为d=
的距离为d=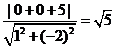


 w_w w. k#s5_
w_w w. k#s5_
故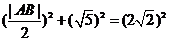 w_w_w.k*s 5*
w_w_w.k*s 5*
得|AB|=2
答案:2
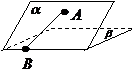 (15)如图,二面角
(15)如图,二面角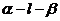 的大小是60°,线段
的大小是60°,线段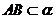 .
.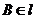 ,
,
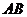 与
与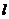 所成的角为30°.则
所成的角为30°.则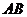 与平面
与平面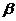 所成的角的正弦值是
.
所成的角的正弦值是
.
解析:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D
连结AD,有三垂线定理可知AD⊥l,
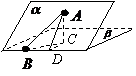 故∠ADC为二面角
故∠ADC为二面角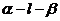 的平面角,为60°
的平面角,为60°
又由已知,∠ABD=30°
连结CB,则∠ABC为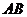 与平面
与平面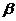 所成的角w_w_w.k*s 5*
所成的角w_w_w.k*s 5*
设AD=2,则AC=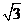 ,CD=1
,CD=1
AB=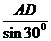 =4
=4
∴sin∠ABC=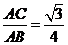
答案: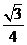
(16)设S为复数集C的非空子集.若对任意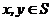 ,都有
,都有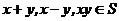 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题:
①集合S={a+bi|(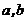 为整数,
为整数,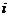 为虚数单位)}为封闭集;w_w_w.k*s 5*
为虚数单位)}为封闭集;w_w_w.k*s 5*
②若S为封闭集,则一定有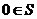 ;
;
③封闭集一定是无限集;
④若S为封闭集,则满足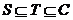 的任意集合
的任意集合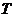 也是封闭集.
也是封闭集. 

 w_w w. k#s5_
w_w w. k#s5_
其中真命题是 (写出所有真命题的序号)
解析:直接验证可知①正确.
当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确
对于集合S={0},显然满足素有条件,但S是有限集,③错误
取S={0},T={0,1},满足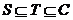 ,但由于0-1=-1ÏT,故T不是封闭集,④错误
,但由于0-1=-1ÏT,故T不是封闭集,④错误
答案:①②
(1)i是虚数单位,计算i+i2+i3=
(A)-1 (B)1
(C)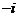 (D)
(D)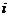
解析:由复数性质知:i2=-1
故i+i2+i3=i+(-1)+(-i)=-1
答案:A
(2)下列四个图像所表示的函数,在点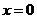 处连续的是
处连续的是
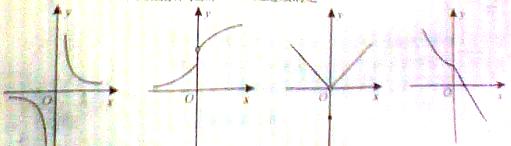
(A) (B) (C) (D)
解析:由图象及函数连续的性质知,D正确.w_w_w.k*s 5*
答案:D
(3)2log510+log50.25=w_w_w.k*s 5*
(A)0 (B)1
(C) 2
(D)4

 w_w w. k#s5_
w_w w. k#s5_
解析:2log510+log50.25
=log5100+log50.25
=log525
=2
答案:C
(4)函数f(x)=x2+mx+1的图像关于直线x=1对称的充要条件是
(A)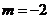 (B)
(B)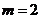 (C)
(C)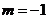 (D)
(D)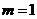
解析:函数f(x)=x2+mx+1的对称轴为x=-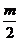 w_w_w.k*s 5*
w_w_w.k*s 5*
于是-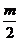 =1 Þ m=-2
=1 Þ m=-2
答案:A
(5)设点M是线段BC的中点,点A在直线BC外,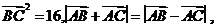 则
则
(A)8 (B)4
(C) 2
(D)1

 w_w w. k#s5_
w_w w. k#s5_
解析:由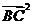 =16,得|BC|=4 w_w_w.k*s 5*
=16,得|BC|=4 w_w_w.k*s 5*
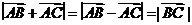 =4
=4
而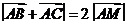
故 2
2
答案:C w_w_w.k*s 5*
(6)将函数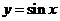 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动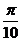 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是

 w_w w. k#s5_
w_w w. k#s5_
(A)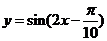 (B)
(B)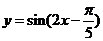 w_w_w.k*s 5*
w_w_w.k*s 5*
(C)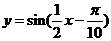 (D)
(D)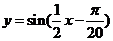
解析:将函数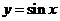 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动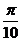 个单位长度,所得函数图象的解析式为y=sin(x-
个单位长度,所得函数图象的解析式为y=sin(x-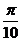 ) w_w_w.k*s 5*
) w_w_w.k*s 5*
再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是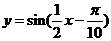 .
.
答案:C
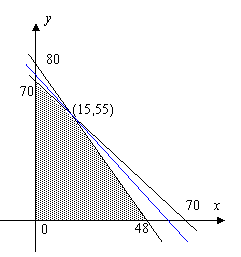 (7)某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为w_w_w.k*s 5*
(7)某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为w_w_w.k*s 5*
(A)甲车间加工原料10箱,乙车间加工原料60箱
(B)甲车间加工原料15箱,乙车间加工原料55箱
(C)甲车间加工原料18箱,乙车间加工原料50箱
(D)甲车间加工原料40箱,乙车间加工原料30箱
解析:设甲车间加工原料x箱,乙车间加工原料y箱
则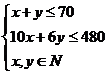


 w_w w. k#s5_
w_w w. k#s5_
目标函数z=280x+300y
结合图象可得:当x=15,y=55时z最大
本题也可以将答案逐项代入检验.
答案:B w_w_w.k*s 5*
(8)已知数列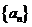 的首项
的首项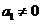 ,其前
,其前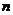 项的和为
项的和为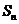 ,且
,且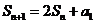 ,则
,则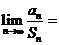
(A)0 (B)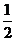 (C) 1
(D)2
(C) 1
(D)2
解析:由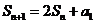 ,且
,且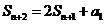 w_w_w.k*s 5*
w_w_w.k*s 5*
作差得an+2=2an+1
又S2=2S1+a1,即a2+a1=2a1+a1 Þ a2=2a1

 w_w w. k#s5_
w_w w. k#s5_
故{an}是公比为2的等比数列
Sn=a1+2a1+22a1+……+2n-1a1=(2n-1)a1
则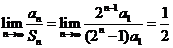
答案:B
(9)椭圆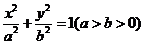 的右焦点
的右焦点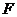 ,其右准线与
,其右准线与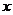 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点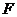 ,则椭圆离心率的取值范围是w_w_w.k*s 5*
,则椭圆离心率的取值范围是w_w_w.k*s 5*
(A)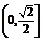 (B)
(B)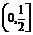 (C)
(C) 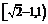 (D)
(D)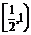
解析:由题意,椭圆上存在点P,使得线段AP的垂直平分线过点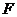 ,
,
即F点到P点与A点的距离相等

 w_w w. k#s5_
w_w w. k#s5_
而|FA|=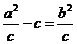 w_w_w.k*s 5*
w_w_w.k*s 5*
|PF|∈[a-c,a+c]
于是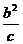 ∈[a-c,a+c]
∈[a-c,a+c]
即ac-c2≤b2≤ac+c2
∴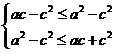
Þ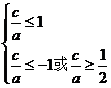 w_w_w.k*s 5*
w_w_w.k*s 5*
又e∈(0,1)
故e∈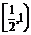
答案:D
(10)由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是
(A)72 (B)96 (C) 108 (D)144 w_w_w.k*s 5*
解析:先选一个偶数字排个位,有3种选法w_w_w.k*s 5*
①若5在十位或十万位,则1、3有三个位置可排,3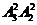 =24个
=24个
②若5排在百位、千位或万位,则1、3只有两个位置可排,共3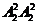 =12个
=12个
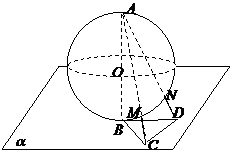 算上个位偶数字的排法,共计3(24+12)=108个
算上个位偶数字的排法,共计3(24+12)=108个
答案:C
(11)半径为 的球
的球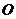 的直径
的直径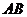 垂直于平面
垂直于平面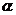 ,垂足为
,垂足为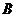 ,
,
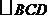 是平面
是平面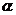 内边长为
内边长为 的正三角形,线段
的正三角形,线段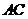 、
、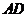 分别
分别
与球面交于点M,N,那么M、N两点间的球面距离是
(A)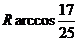 (B)
(B)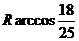 w_w_w.k*s 5*
w_w_w.k*s 5*
(C)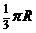 (D)
(D)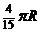
解析:由已知,AB=2R,BC=R,故tan∠BAC=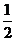 w_w_w.k*s 5*
w_w_w.k*s 5*
cos∠BAC=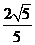
连结OM,则△OAM为等腰三角形
AM=2AOcos∠BAC=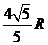 ,同理AN=
,同理AN=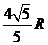 ,且MN∥CD w_w_w.k*s 5*
,且MN∥CD w_w_w.k*s 5*
而AC=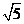 R,CD=R
R,CD=R
故MN:CD=AN:AC w_w_w.k*s 5*
Þ MN= ,
,
连结OM、ON,有OM=ON=R
于是cos∠MON=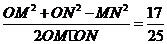
所以M、N两点间的球面距离是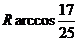 w_w_w.k*s 5*
w_w_w.k*s 5*
答案:A
(12)设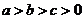 ,则
,则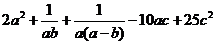 的最小值是
的最小值是

 w_w w. k#s5_
w_w w. k#s5_
(A)2 (B)4 (C) 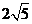 (D)5
(D)5
解析: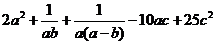
=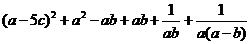 w_w_w.k*s 5*
w_w_w.k*s 5*
=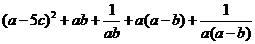
≥0+2+2=4
当且仅当a-5c=0,ab=1,a(a-b)=1时等号成立
如取a=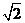 ,b=
,b=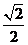 ,c=
,c=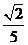 满足条件.
满足条件.
答案:B
第Ⅱ卷
22.(本小题满分14分)
证明以下命题:
(1)对任一正整数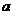 ,都存在正整数
,都存在正整数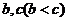 ,使得
,使得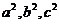 成等差数列;
成等差数列;
(2)存在无穷多个互不相似的三角形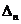 ,其边长
,其边长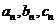 为正整数且
为正整数且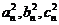 成等差数列.
成等差数列.
21.(本小题满分12分)
设椭圆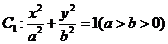 ,抛物线
,抛物线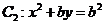 .
.
(1)若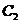 经过
经过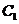 的两个焦点,求
的两个焦点,求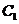 的离心率;(2)设
的离心率;(2)设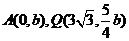 ,又M、N为
,又M、N为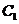 与
与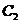 不在
不在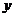 轴上的两个交点,若
轴上的两个交点,若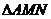 得垂心为
得垂心为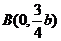 ,且
,且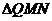 的
的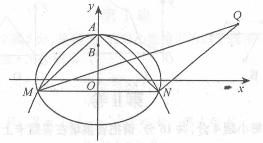 重心在
重心在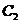 上,求椭圆
上,求椭圆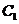 和抛物线
和抛物线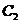 的方程.
的方程.
20.(本小题满分12分)
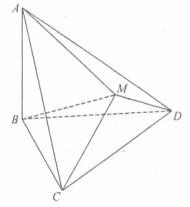
如图,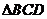 与
与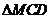 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面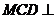 平面
平面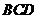 ,
,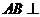 平面BCD,
平面BCD,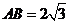 .
.
(1)求点A到平面MBC的距离;
(2)求平面ACM与平面BCD所成二面角的正弦值.
19.(本小题满分12分)
设函数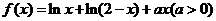 .
.
 (1)当
(1)当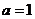 时,求
时,求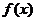 的单调区间;
的单调区间;
(2)若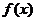 在
在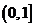 上的最大值为
上的最大值为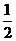 ,求
,求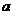 的值.
的值.
18.(本小题满分12分)
某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门.首次到达此门,系统会随机(即等可能)为你打开一个通道.若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走出迷宫为止.令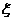 表示走出迷宫所需的时间.
表示走出迷宫所需的时间.
(1)求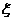 的分布列;(2)求
的分布列;(2)求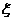 的数学期望.
的数学期望.
17.(本小题满分12分)
已知函数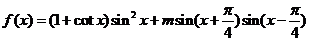 .
.
(1)当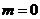 时,求
时,求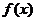 在区间
在区间 上的
上的 取值范围;
取值范围;
(2)当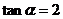 时,
时,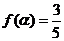 ,求
,求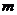 的值.
的值.
16.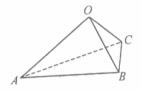 如图,在三棱锥
如图,在三棱锥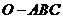 中,三条棱
中,三条棱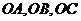 两两垂直,且
两两垂直,且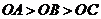 ,分别经过三条棱
,分别经过三条棱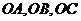 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为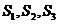 ,则
,则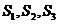 的大小关系为________________.
的大小关系为________________.
15.点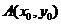 在双曲线
在双曲线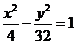 的右支上,若点A到右焦点的距离等于
的右支上,若点A到右焦点的距离等于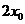 ,则
,则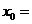 __________.
__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com