
题目列表(包括答案和解析)
12.(2010湖北文数)已知: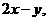 式中变量
式中变量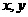 满足的束条件
满足的束条件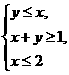 则z的最大值为______。
则z的最大值为______。
[答案]5
[解析]同理科
(2010山东理数)

15.①,③,⑤
[解析]令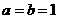 ,排除②②;由
,排除②②;由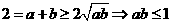 ,命题①正确;
,命题①正确;
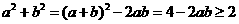 ,命题③正确;
,命题③正确;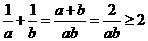 ,命题⑤正确。
,命题⑤正确。
(2010浙江文数)(15)若正实数X,Y 满足2X+Y+6=XY , 则XY 的最小值是 。
答案:18
(2010山东文数)(14)已知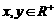 ,且满足
,且满足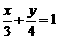 ,则xy的最大值为
.
,则xy的最大值为
.
答案:3
(2010北京文数)(11)若点p(m,3)到直线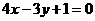 的距离为4,且点p在不等式
的距离为4,且点p在不等式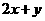 <3表示的平面区域内,则m=
。
<3表示的平面区域内,则m=
。
答案:-3
(2010全国卷1文数)(13)不等式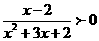 的解集是
.
的解集是
.
13.
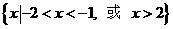 [命题意图]本小题主要考查不等式及其解法
[命题意图]本小题主要考查不等式及其解法
[解析]: 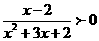
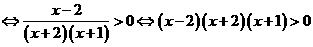 ,数轴标根得:
,数轴标根得: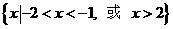
(2010全国卷1理数)(13)不等式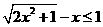 的解集是
.
的解集是
.

2.(2010上海文数)不等式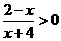 的解集是
的解集是 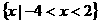 。
。
解析:考查分式不等式的解法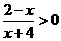 等价于(x-2)(x+4)<0,所以-4<x<2
等价于(x-2)(x+4)<0,所以-4<x<2
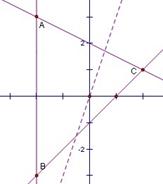 (2010陕西文数)14.设x,y满足约束条件
(2010陕西文数)14.设x,y满足约束条件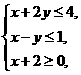 ,则目标函数z=3x-y的最大值为 5 .
,则目标函数z=3x-y的最大值为 5 .
解析:不等式组表示的平面区域如图所示,
当直线z=3x-y过点C(2,1)时,在y轴上截距最小
此时z取得最大值5
(2010辽宁文数)(15)已知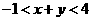 且
且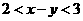 ,则
,则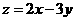 的取值范围是
.
的取值范围是
.
(答案用区间表示)
解析:填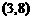 . 利用线性规划,画出不等式组
. 利用线性规划,画出不等式组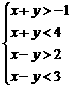 表示的平面区域,即可求解.
表示的平面区域,即可求解.
(2010辽宁理数)(14)已知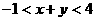 且
且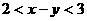 ,则
,则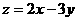 的取值范围是_______(答案用区间表示)
的取值范围是_______(答案用区间表示)
[答案](3,8)
[命题立意]本题考查了线性规划的最值问题,考查了同学们数形结合解决问题的能力。
[解析]画出不等式组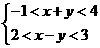 表示的可行域,在可行域内平移直线z=2x-3y,当直线经过x-y=2与x+y=4的交点A(3,1)时,目标函数有最小值z=2×3-3×1=3;当直线经过x+y=-1与x-y=3的焦点A(1,-2)时,目标函数有最大值z=2×1+3×2=8.
表示的可行域,在可行域内平移直线z=2x-3y,当直线经过x-y=2与x+y=4的交点A(3,1)时,目标函数有最小值z=2×3-3×1=3;当直线经过x+y=-1与x-y=3的焦点A(1,-2)时,目标函数有最大值z=2×1+3×2=8.
(2010安徽文数)(15)若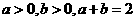 ,则下列不等式对一切满足条件的
,则下列不等式对一切满足条件的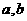 恒成立的是 (写出所有正确命题的编号).
恒成立的是 (写出所有正确命题的编号).
①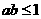 ; ②
; ②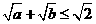 ; ③
; ③ 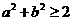 ;
;
④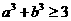 ; ⑤
; ⑤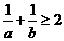
7、(2010江苏卷)右图是一个算法的流程图,则输出S的值是______▲_______

[解析]考查流程图理解。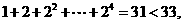 输出
输出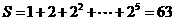 。
。
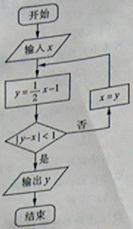 (2010山东理数)(13)执行右图所示的程序框图,若输入
(2010山东理数)(13)执行右图所示的程序框图,若输入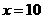 ,则输出
,则输出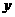 的值为
.
的值为
.
[答案]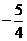
[解析]当x=10时,y=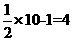 ,此时|y-x|=6;
,此时|y-x|=6;
当x=4时,y=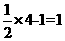 ,此时|y-x|=3;当x=1时,y=
,此时|y-x|=3;当x=1时,y=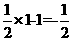 ,此时|y-x|=
,此时|y-x|=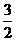 ;
;
当x=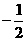 时,y=
时,y=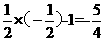 ,此时|y-x|=
,此时|y-x|=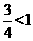 ,故输出y的值为
,故输出y的值为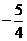 。
。
[命题意图]本题考查程序框图的基础知识,考查了同学们的试图能力。
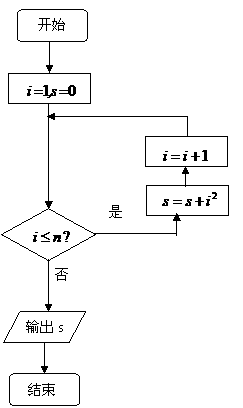 (2010湖南理数)12.图2是求
(2010湖南理数)12.图2是求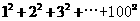
的值的程序框图,则正整数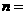 .
.

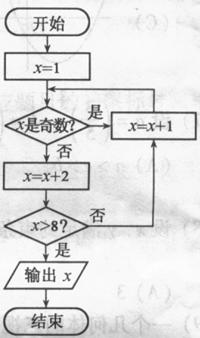 (2010安徽理数)14、如图所示,程序框图(算法流程图)的输出值
(2010安徽理数)14、如图所示,程序框图(算法流程图)的输出值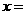 ________。
________。
14.12
[解析]
程序运行如下:
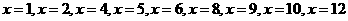 ,
,
输出12。
[规律总结]这类问题,通常由开始一步一步运行,根据判断条件,要么几步后就会输出结果,要么就会出现规律,如周期性,等差或等比数列型.
10.C.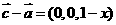 ,
,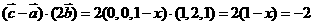 ,解得
,解得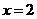 .
.
10.(2010广东理数)若向量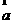 =(1,1,x),
=(1,1,x), 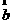 =(1,2,1),
=(1,2,1), 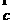 =(1,1,1),满足条件
=(1,1,1),满足条件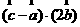 =-2,则
=-2,则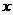 = .
= .
12.(2010陕西文数)已知向量a=(2,-1),b=(-1,m),c=(-1,2)若(a+b)∥c,则
m= -1 .
解析: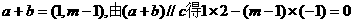 ,所以m=-1
,所以m=-1
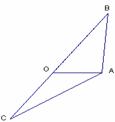 (2010江西理数)13.已知向量
(2010江西理数)13.已知向量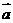 ,
,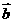 满足
满足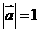 ,
,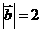 ,
, 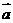 与
与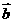 的夹角为60°,则
的夹角为60°,则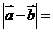
[答案] 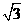
[解析]考查向量的夹角和向量的模长公式,以及向量三角形法则、余弦定理等知识,如图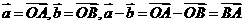 ,由余弦定理得:
,由余弦定理得: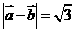
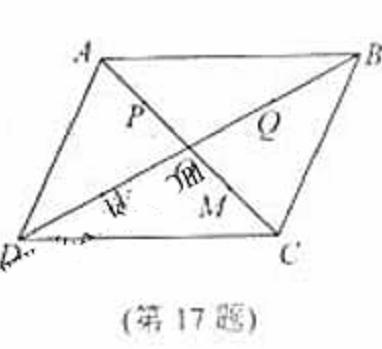
(2010浙江文数)(17)在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量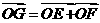 的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 。
的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 。
答案: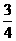
(2010浙江文数)(13)已知平面向量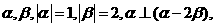 则
则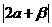 的值是
的值是
答案 :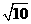
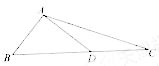 (2010天津理数)(15)如图,在
(2010天津理数)(15)如图,在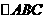 中,
中,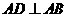 ,
,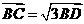 ,
,
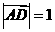 ,则
,则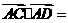 .
.
[答案]D
[解析]本题主要考查平面向量的基本运算与解三角形的基础知识,属于难题。
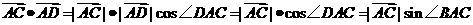
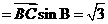
[解析]近几年天津卷中总可以看到平面向量的身影,且均属于中等题或难题,应加强平面向量的基本运算的训练,尤其是与三角形综合的问题。
13.(2010上海文数)在平面直角坐标系中,双曲线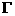 的中心在原点,它的一个焦点坐标为
的中心在原点,它的一个焦点坐标为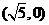 ,
,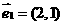 、
、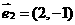 分别是两条渐近线的方向向量。任取双曲线
分别是两条渐近线的方向向量。任取双曲线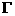 上的点
上的点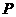 ,若
,若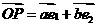 (
(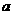 、
、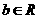 ),则
),则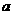 、
、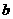 满足的一个等式是 4ab=1
。
满足的一个等式是 4ab=1
。
解析:因为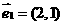 、
、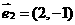 是渐进线方向向量,所以双曲线渐近线方程为
是渐进线方向向量,所以双曲线渐近线方程为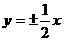 ,又
,又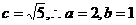
双曲线方程为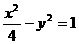 ,
,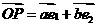 =
=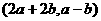 ,
,
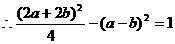 ,化简得4ab=1
,化简得4ab=1
(2010浙江理数)(16)已知平面向量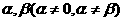 满足
满足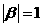 ,且
,且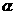 与
与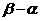 的夹角为120°,则
的夹角为120°,则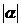 的取值范围是__________________
.
的取值范围是__________________
.
解析:利用题设条件及其几何意义表示在三角形中,即可迎刃而解,本题主要考察了平面向量的四则运算及其几何意义,突出考察了对问题的转化能力和数形结合的能力,属中档题。
15.(2010广东文数)(坐标系与参数方程选做题)在极坐标系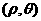
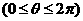 中,曲线
中,曲线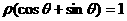 与
与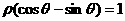 的交点的极坐标为
.
的交点的极坐标为
.
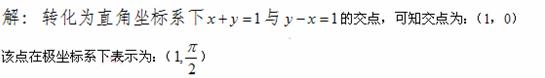
 (2010广东文数)14.(几何证明选讲选做题)如图3,在直角
(2010广东文数)14.(几何证明选讲选做题)如图3,在直角
梯形ABCD中,DC∥AB,CB ,AB=AD=
,AB=AD=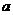 ,CD=
,CD=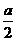 ,
,
点E,F分别为线段AB,AD的中点,则EF=
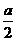
解:连结DE,可知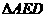 为直角三角形。则EF是
为直角三角形。则EF是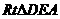 斜边上的中线,等于斜边的一半,为
斜边上的中线,等于斜边的一半,为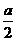 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com