
题目列表(包括答案和解析)
6、(2010辽宁理数)(12) (12)有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架,则a的取值范围是
(A)(0,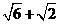 ) (B)(1,
) (B)(1,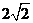 )
)
(C) (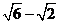 ,
,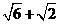 ) (D) (0,
) (D) (0,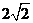 )
)
[答案]A
[命题立意]本题考查了学生的空间想象能力以及灵活运用知识解决数学问题的能力。
[解析]根据条件,四根长为2的直铁条与两根长为a的直铁条要组成三棱镜形的铁架,有以下两种情况:(1)地面是边长为2的正三角形,三条侧棱长为2,a,a,如图,此时a可以取最大值,可知AD=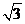 ,SD=
,SD=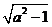 ,则有
,则有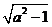 <2+
<2+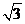 ,即
,即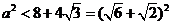 ,即有a<
,即有a<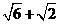
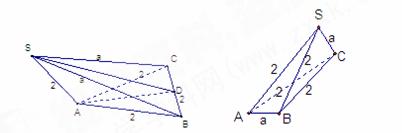
(2)构成三棱锥的两条对角线长为a,其他各边长为2,如图所示,此时a>0;
综上分析可知a∈(0,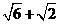 )
)
5、(2010辽宁文数)(11)已知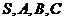 是球
是球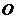 表面上的点,
表面上的点,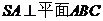 ,
,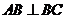 ,
,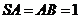 ,
,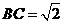 ,则球
,则球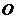 的表面积等于
的表面积等于
(A)4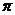 (B)3
(B)3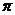 (C)2
(C)2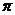 (D)
(D)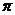
解析:选A.由已知,球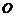 的直径为
的直径为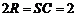 ,
,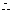 表面积为
表面积为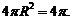
4、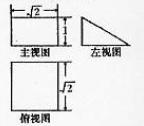 (2010陕西文数) 8.若某空间几何体的三视图如图所示,则该几何体的体积是 [B]
(2010陕西文数) 8.若某空间几何体的三视图如图所示,则该几何体的体积是 [B]
(A)2 (B)1
(C)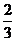 (D)
(D)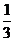
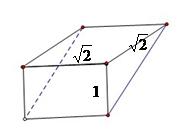
 解析:本题考查立体图形三视图及体积公式
解析:本题考查立体图形三视图及体积公式
如图,该立体图形为直三棱柱
 所以其体积为
所以其体积为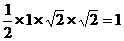
3、(2010全国卷2理数)(9)已知正四棱锥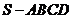 中,
中,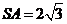 ,那么当该棱锥的体积最大时,它的高为
,那么当该棱锥的体积最大时,它的高为
(A)1
(B)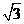 (C)2
(D)3
(C)2
(D)3
[答案]C
[命题意图]本试题主要考察椎体的体积,考察告辞函数的最值问题.
[解析]设底面边长为a,则高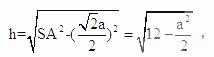 所以体积
所以体积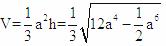 ,
,
设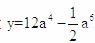 ,则
,则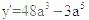 ,当y取最值时,
,当y取最值时,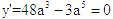 ,解得a=0或a=4时,体积最大,此时
,解得a=0或a=4时,体积最大,此时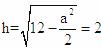 ,故选C.
,故选C.
2、(2010全国卷2理数)(11)与正方体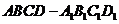 的三条棱
的三条棱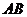 、
、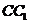 、
、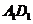 所在直线的距离相等的点
所在直线的距离相等的点
(A)有且只有1个 (B)有且只有2个
(C)有且只有3个 (D)有无数个
[答案]D
[解析]直线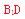 上取一点,分别作
上取一点,分别作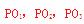 垂直于
垂直于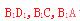 于
于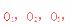 则
则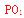

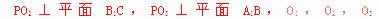 分别作
分别作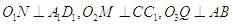 ,垂足分别为M,N,Q,连PM,PN,PQ,由三垂线定理可得,PN⊥
,垂足分别为M,N,Q,连PM,PN,PQ,由三垂线定理可得,PN⊥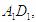 PM⊥
PM⊥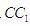 ;PQ⊥AB,由于正方体中各个表面、对等角全等,所以
;PQ⊥AB,由于正方体中各个表面、对等角全等,所以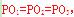
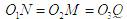 ,∴PM=PN=PQ,即P到三条棱AB、CC1、A1D1.所在直线的距离相等所以有无穷多点满足条件,故选D.
,∴PM=PN=PQ,即P到三条棱AB、CC1、A1D1.所在直线的距离相等所以有无穷多点满足条件,故选D.
1、(2010浙江理数)(6)设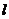 ,
,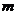 是两条不同的直线,
是两条不同的直线,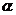 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是
(A)若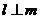 ,
,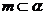 ,则
,则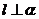 (B)若
(B)若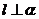 ,
,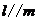 ,则
,则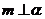
(C)若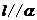 ,
,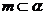 ,则
,则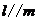 (D)若
(D)若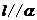 ,
,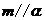 ,则
,则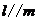
解析:选B,可对选项进行逐个检查。本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理,也蕴含了对定理公理综合运用能力的考察,属中档题
33、(2010安徽卷理)

11.[答案]6
[解析]二项式展开式的通项公式为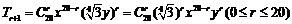 要使系数为有理数,则r必为4的倍数,所以r可为0.、4、8、12、16、20共6种,故系数为有理数的项共有6项.
要使系数为有理数,则r必为4的倍数,所以r可为0.、4、8、12、16、20共6种,故系数为有理数的项共有6项.
32、(2010湖北理数)11、在(x+ 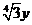 )
)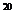 的展开式中,系数为有理数的项共有_______项。
的展开式中,系数为有理数的项共有_______项。
31、(2010湖北文数)11.在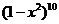 的展开中,
的展开中,
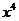 的系数为______。
的系数为______。
[答案]45
[解析]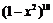 展开式即是10个(1-x2)相乘,要得到x4,则取2个1-x2中的(-x2)相乘,其余选1,则系数为
展开式即是10个(1-x2)相乘,要得到x4,则取2个1-x2中的(-x2)相乘,其余选1,则系数为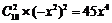 ,故系数为45.
,故系数为45.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com