
题目列表(包括答案和解析)
41、(2010四川理数)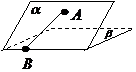 (15)如图,二面角
(15)如图,二面角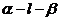 的大小是60°,线段
的大小是60°,线段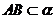 .
.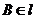 ,
,
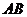 与
与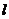 所成的角为30°.则
所成的角为30°.则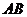 与平面
与平面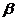 所成的角的正弦值是
.
所成的角的正弦值是
.
解析:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D
连结AD,有三垂线定理可知AD⊥l,
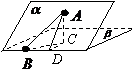 故∠ADC为二面角
故∠ADC为二面角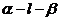 的平面角,为60°
的平面角,为60°
又由已知,∠ABD=30°
连结CB,则∠ABC为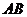 与平面
与平面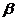 所成的角
所成的角
设AD=2,则AC=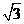 ,CD=1
,CD=1
AB=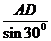 =4
=4
∴sin∠ABC=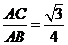
答案: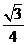
40、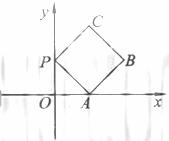 (2010北京理数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
(2010北京理数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的轨迹方程是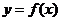 ,则
,则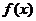 的最小正周期为
;
的最小正周期为
;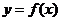 在其两个相邻零点间的图像与x轴所围区域的面积为
在其两个相邻零点间的图像与x轴所围区域的面积为
说明:“正方形PABC沿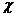 轴滚动”包括沿
轴滚动”包括沿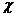 轴正方向和沿
轴正方向和沿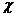 轴负方向滚动。沿
轴负方向滚动。沿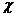 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在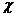 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿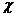 轴负方向滚动。
轴负方向滚动。
答案:4 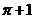
39、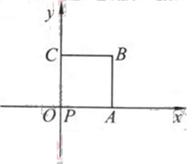 (2010北京文数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
(2010北京文数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的纵坐标与横坐标的函数关系是
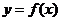 ,则
,则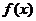 的最小正周期为
;
的最小正周期为
;
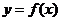 在其两个相邻零点间的图像与x轴
在其两个相邻零点间的图像与x轴
所围区域的面积为 。
说明:“正方形PABC沿x轴滚动”包含沿x轴正方向和沿x轴负方向滚动。沿x轴正方向滚动是指以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,类似地,正方形PABC可以沿着x轴负方向滚动。
答案:4 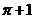
38、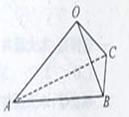 (2010江西理数)16.如图,在三棱锥
(2010江西理数)16.如图,在三棱锥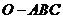 中,三条棱
中,三条棱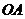 ,
,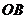 ,
,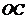 两两垂直,且
两两垂直,且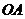 >
>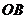 >
>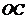 ,分别经过三条棱
,分别经过三条棱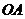 ,
,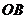 ,
,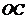 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为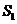 ,
,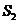 ,
,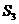 ,则
,则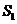 ,
,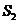 ,
,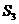 的大小关系为
。
的大小关系为
。
[答案] 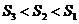
[解析]考查立体图形的空间感和数学知识的运用能力,通过补形,借助长方体验证结论,特殊化,令边长为1,2,3得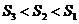 。
。
37、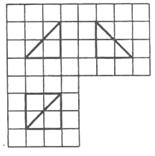 (2010辽宁理数)(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
(2010辽宁理数)(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
[答案]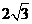
[命题立意]本题考查了三视图视角下多面体棱长的最值问题,考查了同学们的识图能力以及由三视图还原物体的能力。
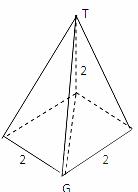
[解析]由三视图可知,此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥,所以最长棱长为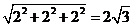
36、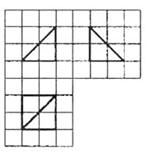 (2010辽宁文数)(16)如图,网格纸的小正方形的边长是1,在其上用粗线画
(2010辽宁文数)(16)如图,网格纸的小正方形的边长是1,在其上用粗线画
出了某多面体的三视图,则这个多面体最长的一条棱的
长为 .
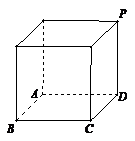 解析:填
解析:填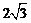 画出直观图:图中四棱锥
画出直观图:图中四棱锥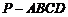 即是,
即是,
所以最长的一条棱的长为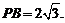
35、(2010浙江理数)(12)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是___________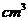 .
.
 解析:图为一四棱台和长方体的组合体的三视图,由卷中所给公式计算得体积为144,本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算,属容易题
解析:图为一四棱台和长方体的组合体的三视图,由卷中所给公式计算得体积为144,本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算,属容易题
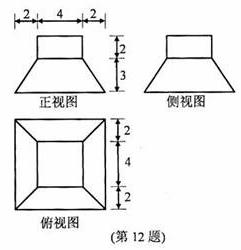
34、(2010湖南文数)13.图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= 4 cm
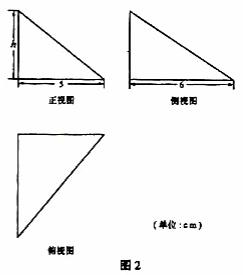
33、(2010上海文数)6.已知四棱椎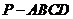 的底面是边长为6 的正方形,侧棱
的底面是边长为6 的正方形,侧棱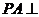 底面
底面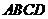 ,且
,且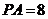 ,则该四棱椎的体积是 96 。
,则该四棱椎的体积是 96 。
解析:考查棱锥体积公式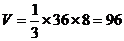
32、(2010福建理数)
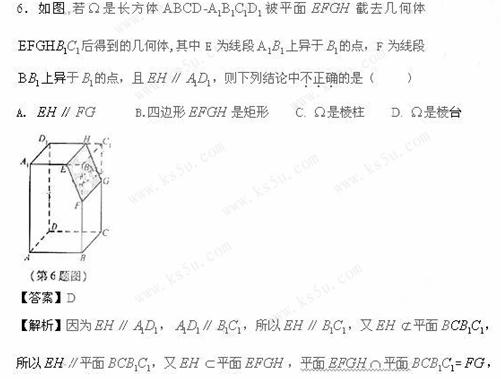
所以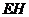 ∥
∥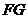 ,故
,故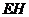 ∥
∥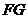 ∥
∥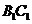 ,所以选项A、C正确;因为
,所以选项A、C正确;因为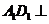 平面
平面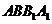 ,
,
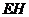 ∥
∥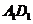 ,所以
,所以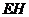
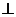 平面
平面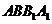 ,又
,又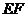
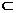 平面
平面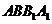 ,
故
,
故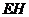
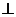
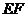 ,所以选项B也正确,故选D。
,所以选项B也正确,故选D。
[命题意图]本题考查空间中直线与平面平行、垂直的判定与性质,考查同学们的空间想象能力和逻辑推理能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com