
题目列表(包括答案和解析)
(1)
(A)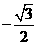 (B)-
(B)-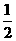 (C)
(C)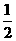 (D)
(D) 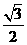
(2)设全集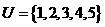 ,集合
,集合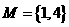 ,
,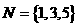 ,则
,则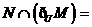
A.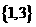 B.
B. 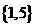 C.
C. 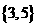 D.
D. 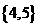
(3)若变量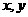 满足约束条件
满足约束条件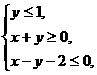 则
则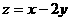 的最大值为
的最大值为
(A)4 (B)3 (C)2 (D)1
(4)已知各项均为正数的等比数列{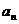 },
},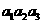 =5,
=5,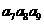 =10,则
=10,则
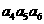 =
=
(A) 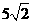 (B) 7 (C) 6 (D)
(B) 7 (C) 6 (D) 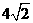
(5)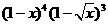 的展开式
的展开式 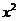 的系数为
的系数为
(A)-6 (B)-3 (C)0 (D)3
(6)直三棱柱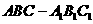 中,若
中,若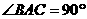 ,
,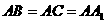 ,则异面直线
,则异面直线
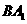 与
与 所成的角等于
所成的角等于
(A)30° (B)45°(C)60° (D)90°
(7)已知函数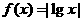 .若
.若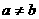 且
且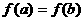 ,则
,则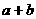 的取值范围是
的取值范围是
(A)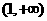 (B)
(B)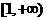 (C)
(C) 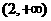 (D)
(D) 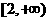
(8)已知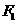 、
、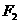 为双曲线C:
为双曲线C: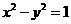 的左、右焦点,点p在C上,∠
的左、右焦点,点p在C上,∠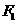 p
p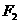 =
= ,则
,则
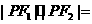
(A)2 (B)4 (C) 6 (D) 8
(9)正方体ABCD-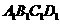 中,B
中,B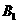 与平面AC
与平面AC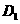 所成角的余弦值为
所成角的余弦值为
(A) 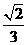 (B)
(B)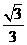 (C)
(C)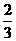 (D)
(D)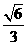
(10)设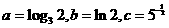 则
则
(A)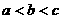 (B)
(B)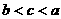 (C)
(C) 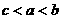 (D)
(D) 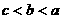
(11)已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么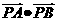 的最小值为
的最小值为
(A) 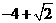 (B)
(B)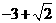 (C)
(C) 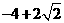 (D)
(D)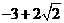
(12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A) 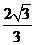 (B)
(B)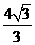 (C)
(C) 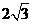 (D)
(D) 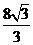
第Ⅱ卷
证号填写清楚,然后贴好条形码。请认真核准条形码上的准考证号、姓名和科目。
2.第Ⅱ卷共2页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域
内作答,在试题卷上作答无效。
21.(本小题满分14分)
已知曲线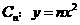 ,点
,点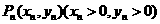 是曲线
是曲线 上的点
上的点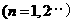 .
.
(1)试写出曲线 在点
在点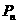 处的切线
处的切线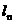 的方程,并求出
的方程,并求出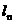 与
与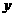 轴的交点
轴的交点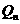 的坐标;
的坐标;
(2)若原点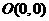 到
到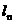 的距离与线段
的距离与线段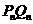 的长度之比取得最大值,试求试点
的长度之比取得最大值,试求试点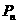 的坐标
的坐标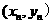 ;
;
(3)设 与
与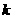 为两个给定的不同的正整数,
为两个给定的不同的正整数,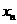 与
与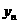 是满足(2)中条件的点
是满足(2)中条件的点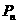 的坐标,
的坐标,
证明: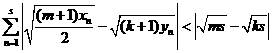
20.(本小题满分14分)
已知函数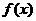 对任意实数
对任意实数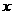 均有
均有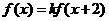 ,其中常数
,其中常数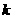 为负数,且
为负数,且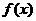 在区间
在区间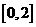 上有表达式
上有表达式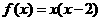 .
.
(1)求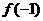 ,
,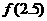 的值;
的值;
(2)写出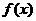 在
在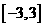 上的表达式,并讨论函数
上的表达式,并讨论函数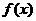 在
在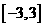 上的单调性;
上的单调性;
(3)求出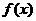 在
在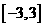 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
19.(本小题满分12分)
某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素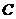 ;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素
;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素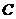 .另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素
.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素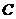 .
.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
18.(本小题满分14分)
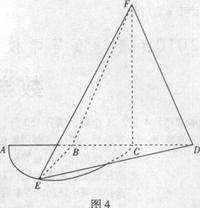 如图4,
如图4,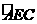 是半径为
是半径为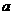 的半圆,
的半圆, 为直径,点
为直径,点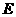 为
为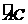 的中点,点
的中点,点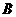 和点
和点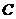 为线段
为线段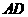 的三等分点,平面
的三等分点,平面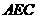 外一点
外一点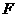 满足
满足
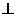 平面
平面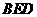 ,
,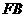 =
=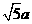 .
.
(1)证明: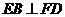 ;
;
(2)求点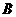 到平面
到平面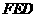 的距离.
的距离.
17.(本小韪满分12分)
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
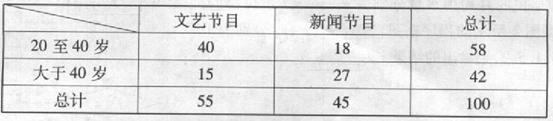
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.
16.(本小题满分l4分)
设函数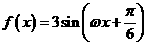 ,
,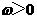 ,
,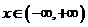 ,且以
,且以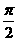 为最小正周期.
为最小正周期.
(1)求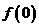 ;
;
(2)求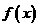 的解析式;
的解析式;
(3)已知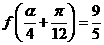 ,求
,求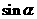 的值.
的值.
15.(坐标系与参数方程选做题)在极坐标系(ρ,θ)( )中,曲线
)中,曲线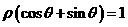 与
与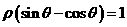 的交点的极坐标为 .
的交点的极坐标为 .
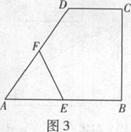
14.(几何证明选讲选做题)如图3,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=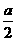 ,点E,F分别为线段AB,CD的中点,则EF= .
,点E,F分别为线段AB,CD的中点,则EF= .
13.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=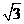 ,A+C=2B,则sinA=
.
,A+C=2B,则sinA=
.
 (二)选做题(14、15题,考生只能从中选做一题)
(二)选做题(14、15题,考生只能从中选做一题)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com