
题目列表(包括答案和解析)
1、(2010江苏卷)设集合A={-1,1,3},B={a+2,a2+4},A∩B={3},则实数a=______▲_____.
[解析] 考查集合的运算推理。3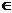 B, a+2=3, a=1.
B, a+2=3, a=1.
11.对任意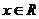 ,都有
,都有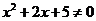 .
.
[解析]特称命题的否定时全称命题,“存在”对应“任意”.
[误区警示]这类问题的常见错误是没有把全称量词改为存在量词,或者对于“>”的否定用“<”了.这里就有注意量词的否定形式.如“都是”的否定是“不都是”,而不是“都不是”.
(2010重庆文数)(11)设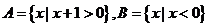 ,则
,则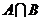 =____________ .
=____________ .
解析: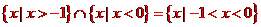
(2010重庆理数)(12)设U=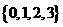 ,A=
,A=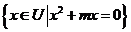 ,若
,若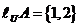 ,则实数m=_________.
,则实数m=_________.
解析: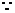
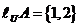 ,
,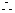 A={0,3},故m= -3
A={0,3},故m= -3
(2010四川理数)(16)设S为复数集C的非空子集.若对任意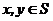 ,都有
,都有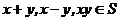 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题:
①集合S={a+bi|(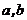 为整数,
为整数,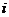 为虚数单位)}为封闭集;w_w_w.k*s 5*
为虚数单位)}为封闭集;w_w_w.k*s 5*
②若S为封闭集,则一定有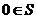 ;
;
③封闭集一定是无限集;
④若S为封闭集,则满足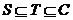 的任意集合
的任意集合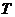 也是封闭集.
也是封闭集. 

 w_w w. k#s5_
w_w w. k#s5_
其中真命题是 (写出所有真命题的序号)
解析:直接验证可知①正确.
当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确
对于集合S={0},显然满足素有条件,但S是有限集,③错误
取S={0},T={0,1},满足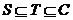 ,但由于0-1=-1ÏT,故T不是封闭集,④错误
,但由于0-1=-1ÏT,故T不是封闭集,④错误
答案:①②
 (2010福建文数)15. 对于平面上的点集
(2010福建文数)15. 对于平面上的点集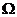 ,如果连接
,如果连接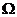 中任意两点的线段必定包含于
中任意两点的线段必定包含于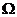 ,则称
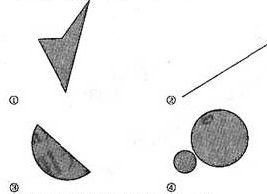
,则称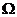 为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
其中为凸集的是 (写出所有凸集相应图形的序号)。
[答案]②③
(2010四川文数)(16)设S为复数集C的非空子集.若对任意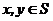 ,都有
,都有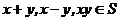 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题:

 w_w w. k#s5_
w_w w. k#s5_
①集合S={a+bi|(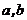 为整数,
为整数,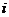 为虚数单位)}为封闭集;
为虚数单位)}为封闭集;
②若S为封闭集,则一定有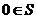 ;
;
③封闭集一定是无限集;
④若S为封闭集,则满足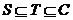 的任意集合
的任意集合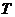 也是封闭集.
也是封闭集.
其中真命题是 (写出所有真命题的序号)
解析:直接验证可知①正确.
当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确
对于集合S={0},显然满足素有条件,但S是有限集,③错误
取S={0},T={0,1},满足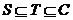 ,但由于0-1=-1ÏT,故T不是封闭集,④错误
,但由于0-1=-1ÏT,故T不是封闭集,④错误
答案:①②

 w_w w. k#s5_
w_w w. k#s5_
9.(2010湖南文数)已知集合A={1,2,3,},B={2,m,4},A∩B={2,3},则m= 3
(2010安徽文数)(11)命题“存在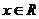 ,使得
,使得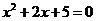 ”的否定是
”的否定是
15.(2010湖南文数)若规定E=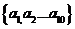 的子集
的子集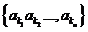 为E的第k个子集,其中k=
为E的第k个子集,其中k=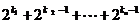 ,则
,则
(1)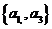 是E的第___5_个子集;
是E的第___5_个子集;
(2)E的第211个子集是___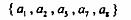 ____
____
1.(2010上海文数)已知集合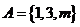 ,
,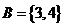 ,
,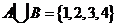 则
则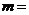 2 。
2 。
解析:考查并集的概念,显然m=2
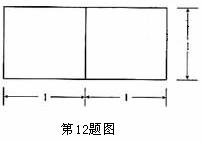
12.若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于 .
[答案]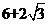
[解析]由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以底面积为
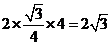 ,侧面积为
,侧面积为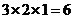 ,所以其表面积为
,所以其表面积为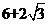 。K^S*5U.C#O%
。K^S*5U.C#O%
[命题意图]本题考查立体几何中的三视图,考查同学们识图的能力、空间想象能力等基本能力。
13.[答案]4
[解析]设球半径为r,则由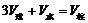 可得
可得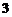
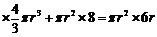 ,解得r=4.
,解得r=4.
(2010福建理数)
13.(2010湖北理数)圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm。
13.(2010湖南理数)图3中的三个直角三角形是 一个体积为20
一个体积为20 的几何体的三视图,则
的几何体的三视图,则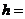
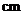 .
.
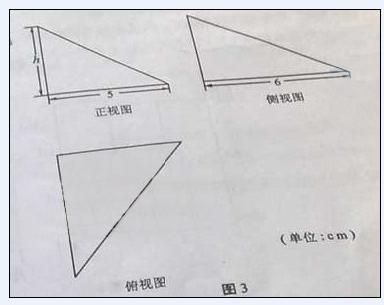


14.(2010湖北文数)圆柱形容器内盛有高度为3cm的水,若放入三个相同的珠(球的半么与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是____cm.
[答案]4
[解析]设球半径为r,则由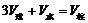 可得
可得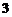
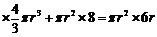 ,解得r=4.
,解得r=4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com