
题目列表(包括答案和解析)
23.选修4-4:坐标系与参数方程
已知曲线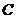 的极坐标方程为
的极坐标方程为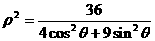 ;
;
(1)若以极点为原点,极轴所在的直线为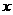 轴,求曲线
轴,求曲线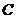 的直角坐标方程;
的直角坐标方程;
(2)若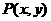 是曲线
是曲线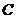 上的一个动点,求
上的一个动点,求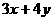 的最大值
的最大值
22.(1)
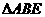 ∽
∽ ,
,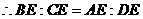 ,
,

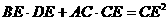 ………3
………3
(2)
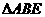 ∽
∽ ,
,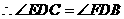 ,
,

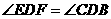 …………6
…………6
(3) AB是⊙O的直径,
AB是⊙O的直径,
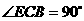 ,
,
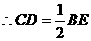 同理,
同理,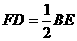 ,
,
所以,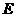 ,
,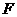 ,
,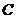 ,
,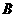 到点
到点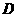 的距离相等,
的距离相等,

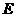 ,
,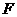 ,
,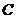 ,
,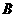 四点共圆 ……10
四点共圆 ……10
22.选修4-1:几何证明选讲
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
 求证:(1)
求证:(1)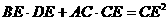 ;
;
(2)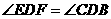 ;
;
(3)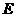 ,
,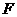 ,
,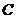 ,
,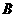 四点共圆
四点共圆
21.解: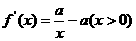 ………1
………1
(1)当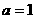 时,
时,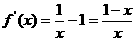
令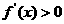 时,解得
时,解得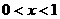 ,所以
,所以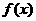 在
在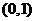 递增;
递增;
令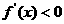 时,解得
时,解得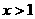 ,所以
,所以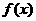 在
在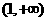 递减 …………………4
递减 …………………4
(2)因为,函数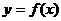 的图像在点
的图像在点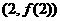 处的切线的倾斜角为
处的切线的倾斜角为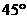 ,
,
所以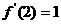 ,
,
所以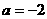 ,
,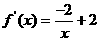 ,………5
,………5
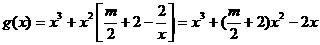 ,
,
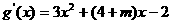 ……6
……6
因为对于任意的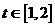 ,
,
函数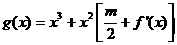 在区间
在区间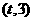 上 总存在极值,
上 总存在极值,
所以只需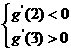 , ………7
, ………7
解得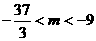 ………8
………8
(3)设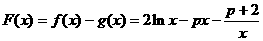
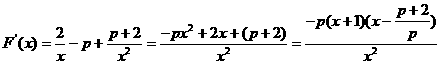 …………9
…………9
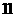
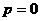 时,
时,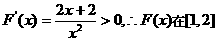 递增,
递增,
所以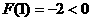 不成立,(舍)
不成立,(舍)
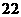
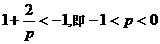 时,同
时,同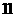 ,不成立,(舍)
,不成立,(舍)
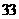
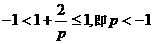 时,
时, 递增,
递增,
所以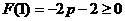 ,解得
,解得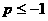
所以,此时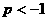
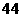
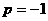 时,
时, 递增,成立;
递增,成立;
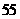
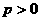 时,均不成立
时,均不成立
综上,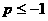 ……12 利用分离变量法求解同样给分
……12 利用分离变量法求解同样给分
21.(本小题满分12分)
已知函数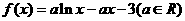
(1)当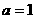 时,求函数
时,求函数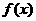 的单调区间;
的单调区间;
(2)若函数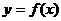 的图像在点
的图像在点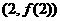 处的切线的倾斜角为
处的切线的倾斜角为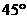 ,问:
,问: 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的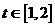 ,函数
,函数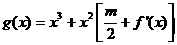 在区间
在区间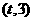 上总存在极值?
上总存在极值?
(3)当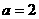 时,设函数
时,设函数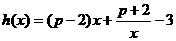 ,若对任意地
,若对任意地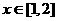 ,
,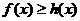 恒成立,求实数
恒成立,求实数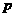 的取值范围
的取值范围
20.(1) 由已知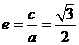 ,所以
,所以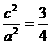 ,所以
,所以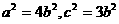
所以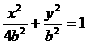 1分
1分
又由过焦点且垂直于长轴的直线被椭圆截得的弦长为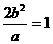
所以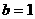 3分
3分
所以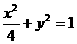 4分
4分
(2)设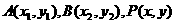
设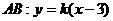 与椭圆联立得
与椭圆联立得

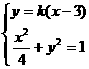
整理得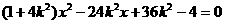
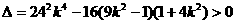
得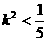
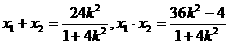 6分
6分
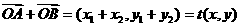
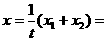
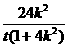
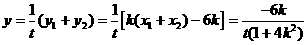
由点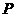 在椭圆上得
在椭圆上得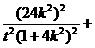
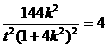
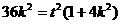 8分
8分
又由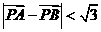 ,即
,即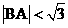
所以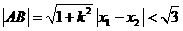 所以
所以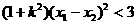
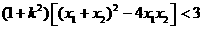
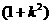
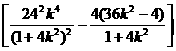
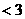
整理得: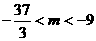
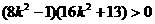
所以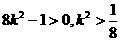 10分
10分
所以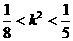 由
由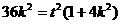 得
得
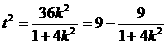
所以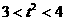 ,所以
,所以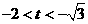 或
或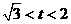 12分
12分
20.(本小题满分12分)
已知椭圆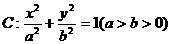 的离心率为
的离心率为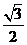 ,过焦点且垂直于长轴的直线被椭圆截得的弦长为
,过焦点且垂直于长轴的直线被椭圆截得的弦长为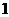 ,过点
,过点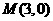 的直线与椭圆
的直线与椭圆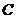 相交于两点
相交于两点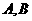 ,
,
(1)求椭圆的方程;
(2)设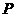 为椭圆上一点,且满足
为椭圆上一点,且满足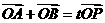 (
( 为坐标原点),当
为坐标原点),当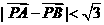 时,求实数
时,求实数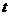 的取值范围
的取值范围
21、解:(1)由题设,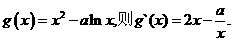 (1分)
(1分)
由已知,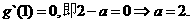 (2分)
(2分)
于是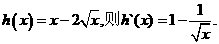 (3分)
(3分)
由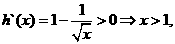 所以
所以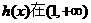 上是增函数,在(0,1)上是减函数。 (4分)
上是增函数,在(0,1)上是减函数。 (4分)
(2)当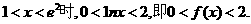 (5分)
(5分)
欲证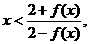 只需证
只需证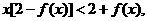 即证
即证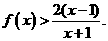 (6分)
(6分)
设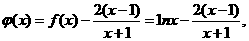
则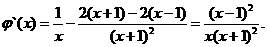
当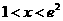 时,
时,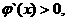 所以
所以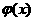 在区间
在区间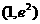 上为增函数。
(7分)
上为增函数。
(7分)
从而当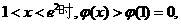 即
即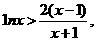 故
故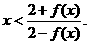 (8分)
(8分)
(3)由题设,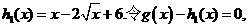
则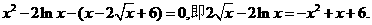 (9分)
(9分)
设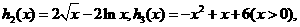
则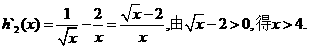
所以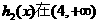 上是增函数,在(0,4)上是减了函数。
(10分)
上是增函数,在(0,4)上是减了函数。
(10分)
 又
又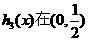 上是增函数,在
上是增函数,在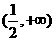 上是减函数。
上是减函数。
因为当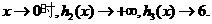
又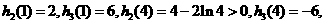
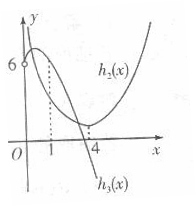
则函数 的大致图象如右:
的大致图象如右:
由图可知,当 两个函数图象有2个交点,故函数
两个函数图象有2个交点,故函数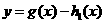 有2个零点。
(13分)
有2个零点。
(13分)
21、(本题13分)给出定义在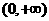 上的三个函数:
上的三个函数: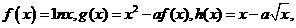 已知
已知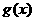 在
在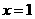 处取得极值。
处取得极值。
(1)确定函数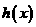 的单调性;
的单调性;
(2)求证:当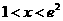 时,恒有
时,恒有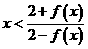 成立;
成立;
(3)把函数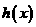 的图象向上平移6个单位长度得到函数
的图象向上平移6个单位长度得到函数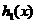 的图象,试确定函数
的图象,试确定函数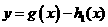 的零点个数,并说明理由。
的零点个数,并说明理由。
20、(1)解:连接PC,由垂径分弦定理知,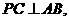 所以点P的轨迹是以线段AC为直径的圆(除去点A)。
所以点P的轨迹是以线段AC为直径的圆(除去点A)。
(2分)
因为点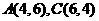 ,则其中点坐标为(5,5),又圆半径
,则其中点坐标为(5,5),又圆半径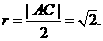
故点P的轨迹方程是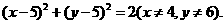 (5分)
(5分)
(2)因为点P、E关于点D(9,0)对称,设点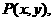 则点
则点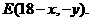 (6分)
(6分)
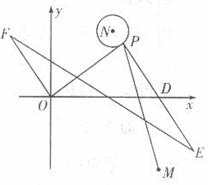 设点
设点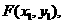 因为线段OF由OP绕原点逆时针旋转90度得到,
因为线段OF由OP绕原点逆时针旋转90度得到,
则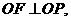 且
且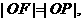 即
即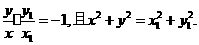
由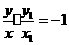 ,得
,得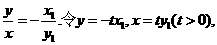
则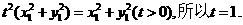 因此点F的坐标为
因此点F的坐标为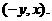
所以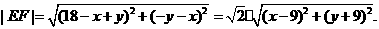
设点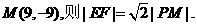 (10分)
(10分)
因为点P为圆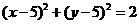 上的点,设圆心为
上的点,设圆心为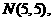
则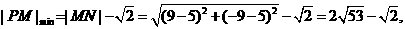
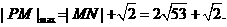 (12分)
(12分)
故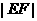 的取值范围是
的取值范围是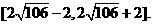 (13分)
(13分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com