
题目列表(包括答案和解析)
20.(本小题满分13分)
已知点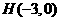 ,点P在
,点P在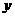 轴上,点
轴上,点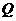 在
在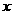 轴的正半轴上,点M在直线PQ上,且满足
轴的正半轴上,点M在直线PQ上,且满足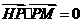 ,
,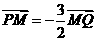 。
。
(I)
当点P在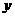 轴上移动时,求点M的轨迹C;
轴上移动时,求点M的轨迹C;
(II)
过点T(-1,0)
作直线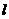 与轨迹C交于A,B两点,若在
与轨迹C交于A,B两点,若在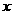 轴上存在一点E(
轴上存在一点E(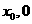 )使得
)使得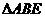 是等边三角形,求
是等边三角形,求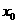 的值。
的值。
19.(本小题满分12分)
设函数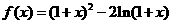
(I)
若对任意的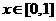 ,不等式
,不等式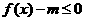 都成立,求实数
都成立,求实数 的最小值;
的最小值;
(II)
求函数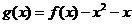 在区间
在区间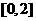 上的极值。
上的极值。
23、解:(1)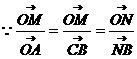 ,…………………………………………2分
,…………………………………………2分
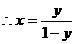 ,从而
,从而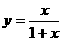 。…………………………………………………4分
。…………………………………………………4分
(2)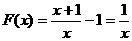 ,
,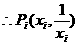 ,又
,又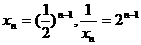 ,
,
…………………………………………………………6分
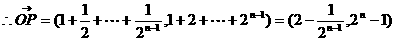 。
。
…………………………………………………………8分
设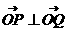 ,则
,则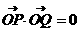 。
。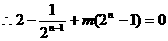 ,
,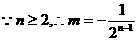 ,
,
故存在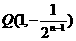 满足条件。…………………………………………………10分
满足条件。…………………………………………………10分
(3)当 时,
时,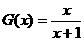 ,又由条件得
,又由条件得
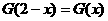 ,
,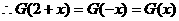 。
。
当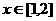 时,
时,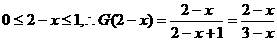 ,
,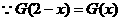 ,
,
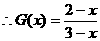 ,从而
,从而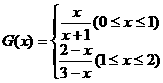 。…………………12分
。…………………12分
由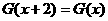 得
得
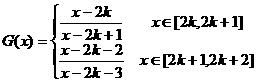 。…………………………14分
。…………………………14分
设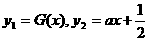 ,在同一直角坐标系中作出两函数的图像,如图
,在同一直角坐标系中作出两函数的图像,如图
当函数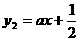 图像经过点
图像经过点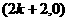 时,
时,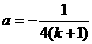 。
。
…………………………………………………………16分
由图像可知,当
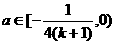 时,
时,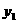 与
与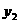 的图像在
的图像在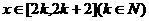 有两个不同交点,因此方程
有两个不同交点,因此方程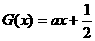 在
在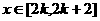 上有两个不同的解。
上有两个不同的解。
…………………………………………………………18分
23、(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形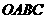 中,已知过点
中,已知过点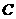 的直线与线段
的直线与线段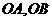 分别相交于点
分别相交于点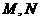 。若
。若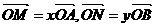 。
。
(1)求证: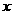 与
与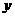 的关系为
的关系为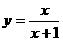 ;
;
(2)设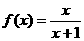 ,定义函数
,定义函数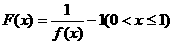 ,点列
,点列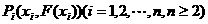 在函数
在函数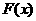 的图像上,且数列
的图像上,且数列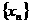 是以首项为1,公比为
是以首项为1,公比为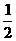 的等比数列,
的等比数列, 为原点,令
为原点,令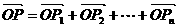 ,是否存在点
,是否存在点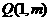
 ,使得
,使得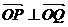 ?若存在,请求出
?若存在,请求出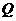 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数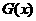 为
为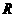 上偶函数,当
上偶函数,当 时
时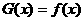 ,又函数
,又函数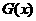 图象关于直线
图象关于直线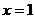 对称, 当方程
对称, 当方程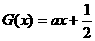 在
在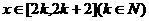 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数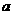 的取值范围。
的取值范围。
22、解:(1)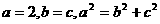 ,
,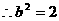 ,
, 椭圆方程为
椭圆方程为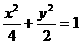 。
。
…………………………………………………………4分
(2)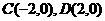 ,设
,设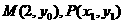 ,则
,则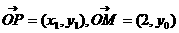 。
。
直线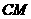 :
: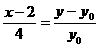 ,即
,即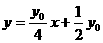 ,……………………………6分
,……………………………6分
代入椭圆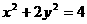 得
得
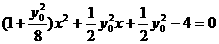 。……………………………………………8分
。……………………………………………8分
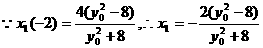 ,
,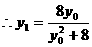 。
。
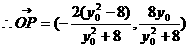 ,………………………………………………10分
,………………………………………………10分

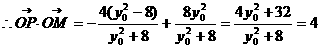 (定值)。
(定值)。
…………………………………………………………12分
(3)设存在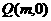 满足条件,则
满足条件,则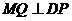 。
。
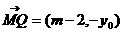 ,
,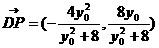 ,…………………………14分
,…………………………14分
则由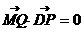 得
得 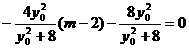 ,从而得
,从而得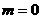 。
。
 存在
存在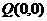 满足条件。…………………………………………………………16分
满足条件。…………………………………………………………16分
22、(本题满分16分,第(1)小题4分,第(2)小题8分,第(3)小题4分)
已知椭圆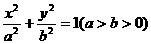 的左右焦点分别为
的左右焦点分别为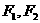 ,短轴两个端点为
,短轴两个端点为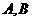 ,且四边形
,且四边形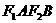 是边长为2的正方形。
是边长为2的正方形。
(1)求椭圆方程;
(2)若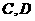 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点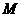 满足
满足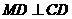 ,连接
,连接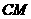 ,交椭圆于点
,交椭圆于点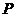 。证明:
。证明: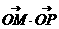 为定值;
为定值;
(3)在(2)的条件下,试问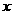 轴上是否存在异于点
轴上是否存在异于点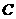 的定点
的定点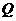 ,使得以
,使得以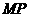 为直径的圆恒过直线
为直径的圆恒过直线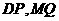 的交点,若存在,求出点
的交点,若存在,求出点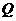 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
21、 解:(1)由题意得,境外游客有27人,其中9人持金卡;境内游客有9人,其中6人持银卡。设事件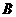 为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件 为“采访该团3人中,1人持金卡,0人持银卡”,
为“采访该团3人中,1人持金卡,0人持银卡”,
事件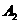 为“采访该团3人中,1人持金卡,1人持银卡”。 .
为“采访该团3人中,1人持金卡,1人持银卡”。 .
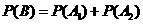
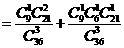 ………………………………………………………3分
………………………………………………………3分
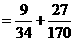
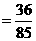
所以在该团中随机采访3人,恰有1人持金卡且持银卡者少于2人的概率是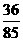 。
。
…………………………………………………………6分
(2)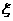 的可能取值为0,1,2,3
的可能取值为0,1,2,3
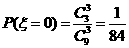 ,
, 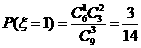 .
.
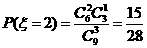 ,
,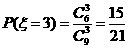 ,. (每个2分)
,. (每个2分)
所以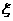 的分布列为
的分布列为
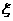 |
0 |
1 |
2 |
3 |
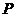 |
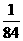 |
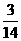 |
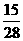 |
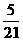 |
…………………………………………………………14分
所以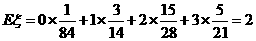 , ……………………16分
, ……………………16分
21、(本题满分16分,第(1)小题6分,第(2)小题10分)
为了让更多的人参与2010年在上海举办的“世博会”,上海某旅游公司面向国内外发行总量为2000万张的旅游优惠卡,其中向境外人士发行的是世博金卡(简称金卡),向境内人士发行的是世博银卡(简称银卡)。现有一个由36名游客组成的旅游团到上海参观旅游,其中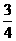 是境外游客,其余是境内游客。在境外游客中有
是境外游客,其余是境内游客。在境外游客中有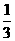 持金卡,在境内游客中有
持金卡,在境内游客中有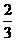 持银卡。.
持银卡。.
(1)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(2)在该团的境内游客中随机采访3名游客,设其中持银卡人数为随机变量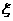 ,求
,求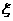 的分布列及数学期望
的分布列及数学期望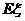 。
。
20、解:(1)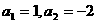 ,
,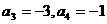 ,
,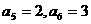 ,
,
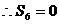 。
…………………………………………………………4分
。
…………………………………………………………4分
(2)由条件得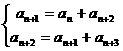 ,
,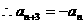 ,………………………6分
,………………………6分
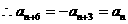 ,即
,即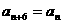 。………………………………………8分
。………………………………………8分
(3)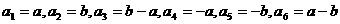 。
。
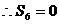 。
…………………………………………………………10分
。
…………………………………………………………10分
由(2)得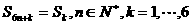 。………………………………12分
。………………………………12分
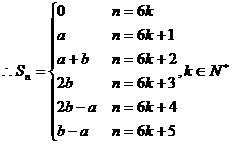 ………………………………………14分
………………………………………14分
20、(本题满分14分,第(1)小题4分,第(2)小题4分,第(2)小题6分)
设数列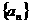 中,若
中,若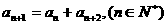 ,则称数列
,则称数列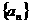 为“凸数列”。
为“凸数列”。
(1)设数列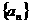 为“凸数列”,若
为“凸数列”,若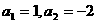 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;
(2)在“凸数列”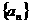 中,求证:
中,求证: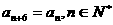 ;
;
(3)设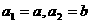 ,若数列
,若数列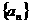 为“凸数列”,求数列前
为“凸数列”,求数列前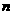 项和
项和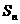 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com