
题目列表(包括答案和解析)
8.(湖北卷理17)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=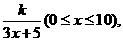 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。


7.(广东卷文21)已知曲线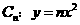 ,点
,点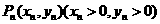 是曲线
是曲线 上的点(n=1,2,…).
上的点(n=1,2,…).
(1)试写出曲线 在点
在点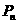 处的切线
处的切线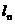 的方程,并求出
的方程,并求出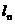 与
与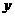 轴的交点
轴的交点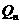 的坐标;
的坐标;
(2)若原点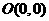 到
到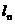 的距离与线段
的距离与线段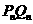 的长度之比取得最大值,试求试点
的长度之比取得最大值,试求试点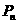 的坐标
的坐标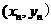 ;
;
(3)设 与
与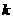 为两个给定的不同的正整数,
为两个给定的不同的正整数,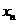 与
与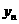 是满足(2)中条件的点
是满足(2)中条件的点 的坐标,
的坐标,
证明: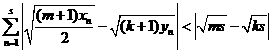
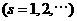
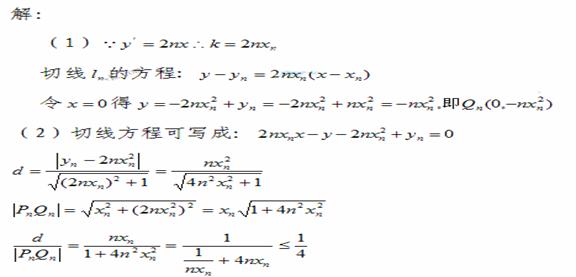
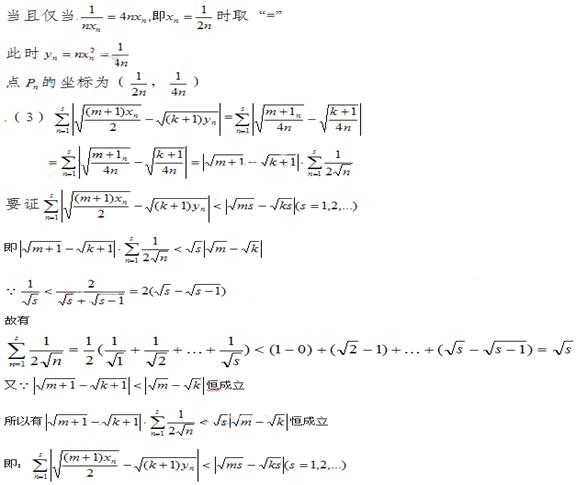
6.(福建卷文22)已知函数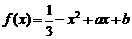 的图像在点P(0,f(0))处的切线方程为
的图像在点P(0,f(0))处的切线方程为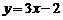 .
.
(Ⅰ)求实数a,b的值;
(Ⅱ)设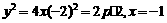
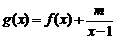 是
是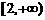 上的增函数.
上的增函数.
(ⅰ)求实数m的最大值;
(ⅱ)当m取最大值时,是否存在点Q,使得过点Q的直线能与曲线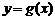 围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.




5.
 (福建卷理20)
(福建卷理20)
(Ⅰ)已知函数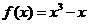 ,其图象记为曲线
,其图象记为曲线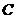 。
。
(ⅰ)求函数 的单调区间;
的单调区间;
(ⅱ)证明:若对于任意非零实数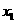 ,曲线
,曲线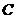 与其在点
与其在点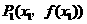 处的切线交于另一点
处的切线交于另一点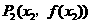 ,曲线
,曲线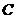 与其在点
与其在点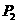 处的切线交于另一点
处的切线交于另一点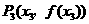 ,线段
,线段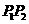 、
、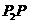 与曲线
与曲线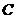 所围成封闭图形的面积分别记为S1,S2,则
所围成封闭图形的面积分别记为S1,S2,则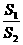 为定值;
为定值;
(Ⅱ)对于一般的三次函数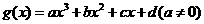 ,请给出类似于(Ⅰ)(ii)的正确命题,并予以证明。
,请给出类似于(Ⅰ)(ii)的正确命题,并予以证明。
[命题意图]本小题主要考查函数、导数、定积分等基础知识,考查抽象概括能力、运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想、特殊与一般思想。
[解析](Ⅰ)(i)由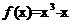 得
得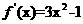 =
=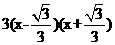 ,
,
当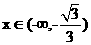 和
和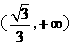 时,
时,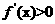 ;
;
当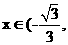
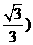 时,
时,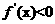 ,
,
因此,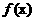 的单调递增区间为
的单调递增区间为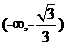 和
和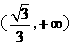 ,单调递减区间为
,单调递减区间为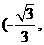
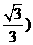 。
。
(ii)曲线C与其在点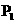 处的切线方程为
处的切线方程为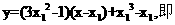
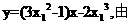
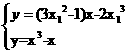 得
得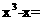
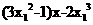 ,
,
即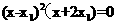 ,解得
,解得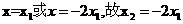 ,进而有
,进而有
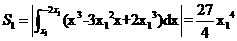 ,用
,用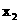 代替
代替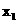 ,重复上述计算过程,可得
,重复上述计算过程,可得
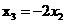 和
和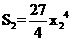 ,又
,又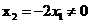 ,所以
,所以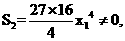
因此有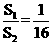 。
。
(Ⅱ)记函数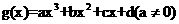 的图象为曲线
的图象为曲线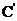 ,类似于(Ⅰ)(ii)的正确命题为:若对任意不等式
,类似于(Ⅰ)(ii)的正确命题为:若对任意不等式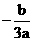 的实数
的实数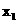 ,曲线
,曲线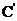 与其在点
与其在点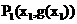 处的切线交于另一点
处的切线交于另一点
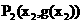 ,曲线C与其在点
,曲线C与其在点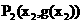 处的切线交于另一点
处的切线交于另一点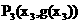 ,线段
,线段

证明如下:
因为平移变换不改变面积的大小,故可将曲线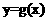 的对称中心
的对称中心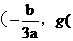
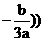 平移至坐标原点,因而不妨设
平移至坐标原点,因而不妨设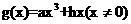 ,类似(i)(ii)的计算可得
,类似(i)(ii)的计算可得
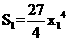 ,
,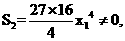 故
故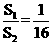 。
。
4.(北京卷文18)设定函数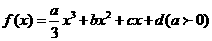 ,且方程
,且方程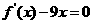 的两个根分别为1,4。
的两个根分别为1,4。
(Ⅰ)当a=3且曲线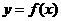 过原点时,求
过原点时,求 的解析式;
的解析式;
(Ⅱ)若 在
在 无极值点,求a的取值范围。
无极值点,求a的取值范围。
3.(北京卷理18)已知函数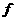 (
(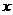 )=In(1+
)=In(1+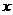 )-
)-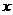 +
+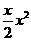 (
(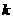 ≥0)。
≥0)。
(Ⅰ)当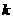 =2时,求曲线
=2时,求曲线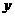 =
=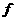 (
(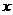 )在点(1,
)在点(1,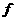 (1))处的切线方程;
(1))处的切线方程;
(Ⅱ)求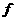 (
(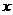 )的单调区间。
)的单调区间。
解:(I)当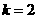 时,
时,
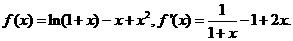
由于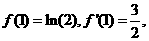 所以曲线
所以曲线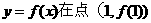 处的切线方程为
处的切线方程为
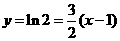 。即
。即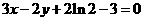
(II)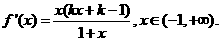 当
当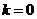 时,
时,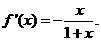
因此在区间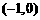 上,
上,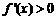 ;在区间
;在区间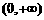 上,
上,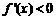 ;
;
所以 的单调递增区间为
的单调递增区间为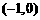 ,单调递减区间为
,单调递减区间为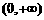 ;
;
当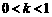 时,
时,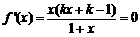 ,得
,得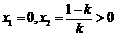 ;
;
因此,在区间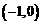 和
和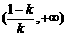 上,
上,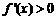 ;在区间
;在区间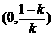 上,
上,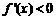 ;
;
即函数  的单调递增区间为
的单调递增区间为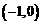 和
和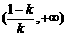 ,单调递减区间为
,单调递减区间为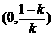 ;
;
当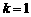 时,
时,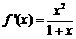 .
. 的递增区间为
的递增区间为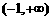
当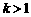 时,由
时,由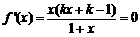 ,得
,得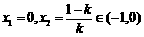 ;
;
因此,在区间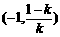 和
和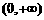 上,
上,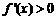 ,在区间
,在区间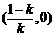 上,
上,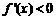 ;
;
即函数  的单调递增区间为
的单调递增区间为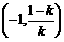 和
和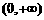 ,单调递减区间为
,单调递减区间为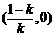 。
。
2.(安徽卷文20)设函数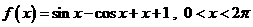 ,求函数
,求函数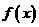 的单调区间与极值。
的单调区间与极值。
[命题意图]本题考查导数的运算,利用导数研究函数的单调性与极值的方法,考查综合应用数学知识解决问题的能力.
[解题指导](1)对函数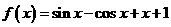 求导,对导函数用辅助角公式变形,利用导数等于0得极值点,通过列表的方法考查极值点的两侧导数的正负,判断区间的单调性,求极值.
求导,对导函数用辅助角公式变形,利用导数等于0得极值点,通过列表的方法考查极值点的两侧导数的正负,判断区间的单调性,求极值.

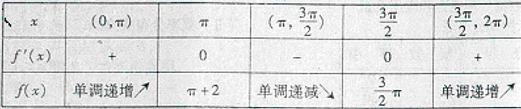

[思维总结]对于函数解答题,一般情况下都是利用导数来研究单调性或极值,利用导数为0得可能的极值点,通过列表得每个区间导数的正负判断函数的单调性,进而得出极值点.
1.(安徽卷理17)设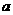 为实数,函数
为实数,函数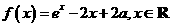 。
。
(Ⅰ)求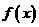 的单调区间与极值;
的单调区间与极值;
(Ⅱ)求证:当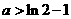 且
且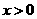 时,
时,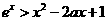 。
。


4.(浙江卷文16)某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少至少达7000万元,则,x 的最小值 。
解析:20;依题意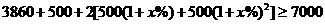 ,化简得
,化简得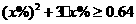 ,所以
,所以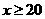 。
。
[命题意图]本题主要考察了用一元二次不等式解决实际问题的能力,属中档题
3.(上海卷文9)函数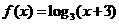 的反函数的图像与
的反函数的图像与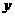 轴的交点坐标是 。
轴的交点坐标是 。
解析:考查反函数相关概念、性质
法一:函数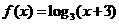 的反函数为
的反函数为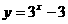 ,另x=0,有y=-2
,另x=0,有y=-2
法二:函数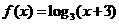 图像与x轴交点为(-2,0),利用对称性可知,函数
图像与x轴交点为(-2,0),利用对称性可知,函数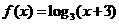 的反函数的图像与
的反函数的图像与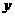 轴的交点为(0,-2)
轴的交点为(0,-2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com