
题目列表(包括答案和解析)
(三)例题分析:
例1.判断下列各函数的奇偶性:
(1)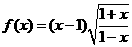 ;(2)
;(2)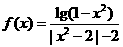 ;
;
(3)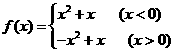 .
.
解:(1)由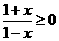 ,得定义域为
,得定义域为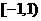 ,关于原点不对称,∴
,关于原点不对称,∴ 为非奇非偶函数.
为非奇非偶函数.
(2)由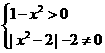 得定义域为
得定义域为 ,
,
∴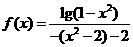
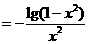 ,
,
 ∵
∵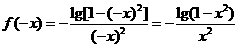
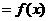 ∴
∴ 为偶函数
为偶函数
(3)当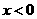 时,
时, ,则
,则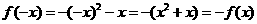 ,
,
当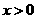 时,
时,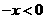 ,则
,则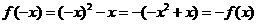 ,
,
综上所述,对任意的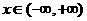 ,都有
,都有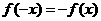 ,∴
,∴ 为奇函数.
为奇函数.
例2.已知函数 对一切
对一切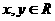 ,都有
,都有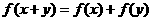 ,
,
(1)求证: 是奇函数;(2)若
是奇函数;(2)若 ,用
,用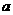 表示
表示 .
.
解:(1)显然 的定义域是
的定义域是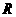 ,它关于原点对称.在
,它关于原点对称.在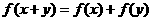 中,
中,
令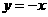 ,得
,得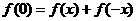 ,令
,令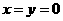 ,得
,得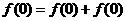 ,
,
∴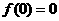 ,∴
,∴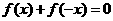 ,即
,即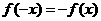 , ∴
, ∴ 是奇函数.
是奇函数.
(2)由 ,
,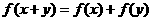 及
及 是奇函数,
是奇函数,
得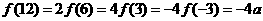 .
.
例3.(1)已知 是
是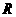 上的奇函数,且当
上的奇函数,且当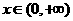 时,
时,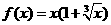 ,
,
则 的解析式为
的解析式为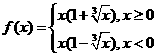 .
.
(2) (《高考 计划》考点3“智能训练第4题”)已知
计划》考点3“智能训练第4题”)已知 是偶函数,
是偶函数,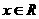 ,当
,当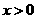 时,
时, 为增函数,若
为增函数,若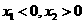 ,且
,且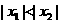 ,则
(
,则
( 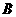 )
)
 .
.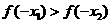
 .
.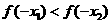
 .
.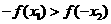
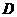 .
. 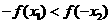
例4.设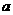 为实数,函数
为实数,函数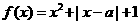 ,
,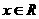 .
.
(1)讨论 的奇偶性; (2)求
的奇偶性; (2)求  的最小值.
的最小值.
解:(1)当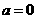 时,
时,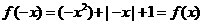 ,此时
,此时 为偶函数;
为偶函数;
当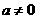 时,
时,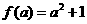 ,
,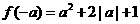 ,
,
∴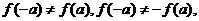
此时函数 既不是奇函数也不是偶函数.
既不是奇函数也不是偶函数.
(2)①当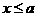 时,函数
时,函数 ,
,
若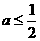 ,则函数
,则函数 在
在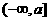 上单调递减,∴函数
上单调递减,∴函数 在
在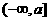 上的最小值为
上的最小值为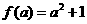 ;
;
若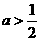 ,函数
,函数 在
在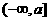 上的最小值为
上的最小值为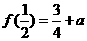 ,且
,且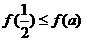 .
.
②当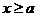 时,函数
时,函数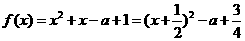 ,
,
若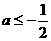 ,则函数
,则函数 在
在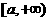 上的最小值为
上的最小值为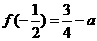 ,且
,且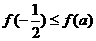 ;
;
若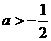 ,则函数
,则函数 在
在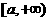 上单调递增,∴函数
上单调递增,∴函数 在
在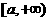 上的最小值
上的最小值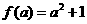 .
.
综上,当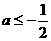 时,函数
时,函数 的最小值是
的最小值是 ,当
,当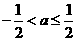 时,函数
时,函数 的最小值是
的最小值是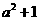 ,
,
当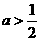 ,函数
,函数 的最小值是
的最小值是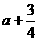 .
.
例5.(《高考 计划》考点3“智能训练第15题”)
计划》考点3“智能训练第15题”)
已知 是定义在实数集
是定义在实数集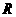 上的函数,满足
上的函数,满足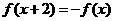 ,且
,且 时,
时,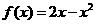 ,
,
(1)求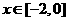 时,
时, 的表达式;(2)证明
的表达式;(2)证明 是
是 上的奇函数.
上的奇函数.
(参见《高考 计划》教师用书
计划》教师用书 )
)
(二)主要方法:
1.判断函数的奇偶性,首先要研究函数的定义域,有时还要对函数式化简整理,但必须注意使定义域不受影响;
2.牢记奇偶函数的图象特征,有助于判断函数的奇偶性;
3.判断函数的奇偶性有时可以用定义的等价形式: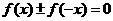 ,
,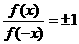 .
.
4.设 ,
,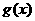 的定义域分别是
的定义域分别是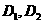 ,那么在它们的公共定义域上:
,那么在它们的公共定义域上:
奇+奇=奇,奇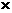 奇=偶,偶+偶=偶,偶
奇=偶,偶+偶=偶,偶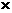 偶=偶,奇
偶=偶,奇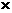 偶=奇.
偶=奇.
5.注意数形结合思想的应用.
(一)主要知识:
1.函数的奇偶性的定义;
2.奇偶函数的性质:
(1)定义域关于原点对称;(2)偶函数的图象关于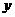 轴对称,奇函数的图象关于原点对称;
轴对称,奇函数的图象关于原点对称;
3. 为偶函数
为偶函数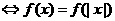 .
.
4.若奇函数 的定义域包含
的定义域包含 ,则
,则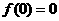 .
.
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.《高考 计划》考点11,智能训练10;
计划》考点11,智能训练10;
2.已知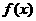 是
是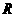 上的奇函数,且在
上的奇函数,且在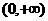 上是增函数,则
上是增函数,则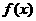 在
在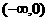 上的单调性为 .
上的单调性为 .
(三)例题分析:
例1.(1)求函数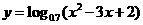 的单调区间;
的单调区间;
(2)已知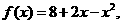 若
若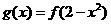 试确定
试确定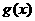 的单调区间和单调性.
的单调区间和单调性.
解:(1)单调增区间为: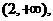 单调减区间为
单调减区间为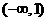 ,
,
(2)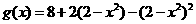
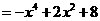 ,
,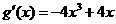 ,
,
令 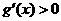 ,得
,得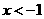 或
或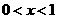 ,令
,令 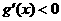 ,
,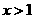 或
或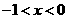
∴单调增区间为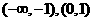 ;单调减区间为
;单调减区间为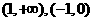 .
.
例2.设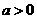 ,
,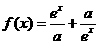 是
是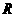 上的偶函数.
上的偶函数.
(1)求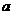 的值;(2)证明
的值;(2)证明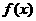 在
在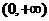 上为增函数.
上为增函数.
解:(1)依题意,对一切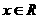 ,有
,有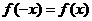 ,即
,即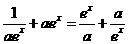
∴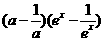
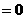 对一切
对一切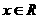 成立,则
成立,则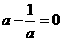 ,∴
,∴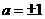 ,∵
,∵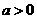 ,∴
,∴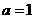 .
.
(2)设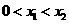 ,则
,则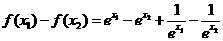
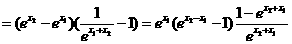 ,
,
由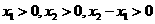 ,得
,得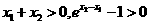 ,
,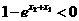 ,
,
∴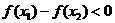 ,
,
即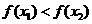 ,∴
,∴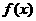 在
在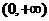 上为增函数.
上为增函数.
例3.(1)(《高考 计划》考点11“智能训练第9题”)若
计划》考点11“智能训练第9题”)若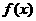 为奇函数,且在
为奇函数,且在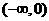 上是减函数,又
上是减函数,又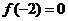 ,则
,则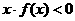 的解集为
的解集为 .
.
例4.(《高考 计划》考点10智能训练14)已知函数
计划》考点10智能训练14)已知函数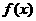 的定义域是
的定义域是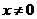 的一切实数,对定义域内的任意
的一切实数,对定义域内的任意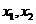 都有
都有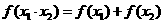 ,且当
,且当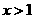 时
时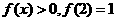 ,
,
(1)求证: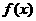 是偶函数;(2)
是偶函数;(2)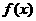 在
在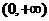 上是增函数;(3)解不等式
上是增函数;(3)解不等式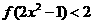 .
.
解:(1)令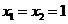 ,得
,得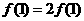 ,∴
,∴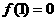 ,令
,令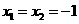 ,得∴
,得∴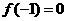 ,
,
∴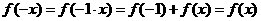 ,∴
,∴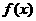 是偶函数.
是偶函数.
(2)设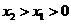 ,则
,则
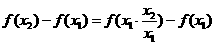
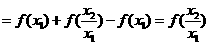
∵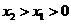 ,∴
,∴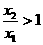 ,∴
,∴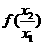
 ,即
,即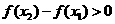 ,∴
,∴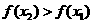
∴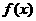 在
在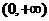 上是增函数.
上是增函数.
(3)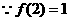 ,∴
,∴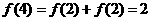 ,
,
∵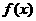 是偶函数∴不等式
是偶函数∴不等式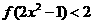 可化为
可化为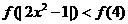 ,
,
又∵函数在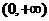 上是增函数,∴
上是增函数,∴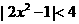 ,解得:
,解得: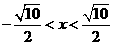 ,
,
即不等式的解集为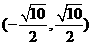 .
.
例5.函数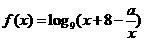 在
在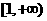 上是增函数,求
上是增函数,求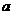 的取值范围.
的取值范围.
分析:由函数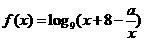 在
在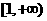 上是增函数可以得到两个信息:①对任意的
上是增函数可以得到两个信息:①对任意的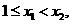 总有
总有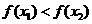 ;②当
;②当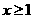 时,
时,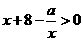 恒成立.
恒成立.
解:∵函数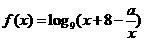 在
在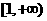 上是增函数,∴对任意的
上是增函数,∴对任意的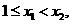 有
有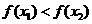 ,即
,即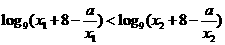 ,得
,得
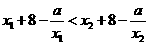 ,即
,即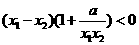 ,
,
∵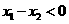 ,∴
,∴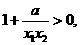
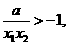
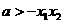 ,
,
∵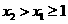 ,∴要使
,∴要使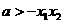 恒成立,只要
恒成立,只要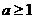 ;
;
又∵函数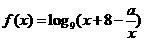 在
在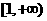 上是增函数,∴
上是增函数,∴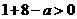 ,
,
即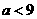 ,综上
,综上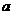 的取值范围为
的取值范围为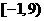 .
.
另解:(用导数求解)令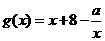 ,函数
,函数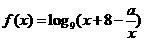 在
在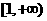 上是增函数,
上是增函数,
∴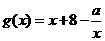 在
在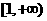 上是增函数,
上是增函数,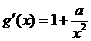 ,
,
∴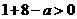 ,且
,且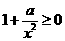 在
在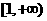 上恒成立,得
上恒成立,得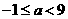 .
.
(二)主要方法:
1.讨论函数单调性必须在其定义域内进行,因此要研究函数单调性必须先求函数的定义域,函数的单调区间是定义域的子集;
2.判断函数的单调性的方法有:(1)用定义;(2)用已知函数的单调性;(3)利用函数的导数.
3.注意函数的单调性的应用;
4.注意分类讨论与数形结合的应用.
(一)主要知识:
1.函数单调性的定义;
2.判断函数的单调性的方法;求函数的单调区间;
3.复合函数单调性的判断.
11.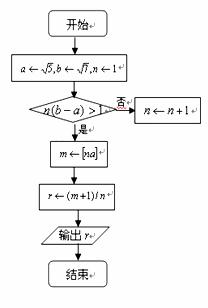 (上海春卷12)根据所示的程序框图(其中
(上海春卷12)根据所示的程序框图(其中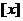 表示不大于x[来源:学的最大整数),输出r=__________。
表示不大于x[来源:学的最大整数),输出r=__________。
答案:
解析:由框图的算法原理可知: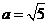 ,
,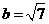 ,
,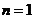 ,
,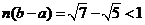 ;
;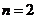 ,
,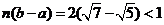 ;
;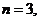
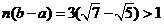 ,
, ,
,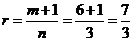 ,输出
,输出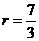 。
。
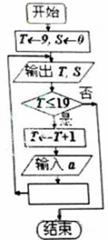
9.(山东卷文13)执行右图所示的程序框图,若输入 ,则输出y的值为
,则输出y的值为
[答案]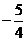
[解析]当x=4时,y=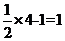 ,此时|y-x|=3;当x=1时,y=
,此时|y-x|=3;当x=1时,y=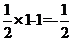 ,此时|y-x|=
,此时|y-x|=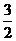 ;
;
当x=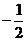 时,y=
时,y=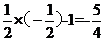 ,此时|y-x|=
,此时|y-x|=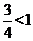 ,故输出y的值为
,故输出y的值为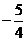 。
。
[命题意图]本题考查程序框图的基础知识,考查了同学们的试图能力。
 10(上海卷理7文11)2010年上海世博会园区每天9:00开园,20:00停止入园。在右边的框图中,
10(上海卷理7文11)2010年上海世博会园区每天9:00开园,20:00停止入园。在右边的框图中,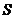 表示上海世博会官方网站在每个整点报道的入园总人数,
表示上海世博会官方网站在每个整点报道的入园总人数,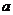 表示整点报道前1个小时内入园人数,则空白的执行框内应填入
表示整点报道前1个小时内入园人数,则空白的执行框内应填入

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com