
题目列表(包括答案和解析)
8. 若对一切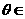 R,复数
R,复数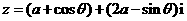 的模不超过2,则实数
的模不超过2,则实数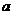 的取值范围为
的取值范围为
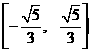
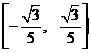 A.
A. 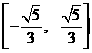 B.
C.
B.
C. 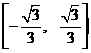 D.
D.
7. 已知两不共线向量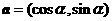 ,
,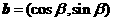 ,则下列说法不正确的是
,则下列说法不正确的是
A.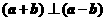 B.
B. 与
与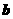 的夹角等于
的夹角等于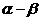
C.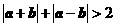 D.
D. 与
与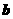 在
在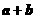 方向上的投影相等
方向上的投影相等
6. 设A1、A2为椭圆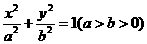 的左右顶点,若在椭圆上存在异于A1、A2的
的左右顶点,若在椭圆上存在异于A1、A2的
点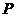 ,使得
,使得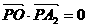 ,其中O为坐标原点,则椭圆的离心率
,其中O为坐标原点,则椭圆的离心率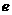 的取值范围是( )
的取值范围是( )
A、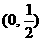 B、
B、 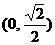 C、
C、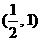 D、
D、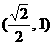
5. 吴同学晨练所花时间(单位:分钟)分别为x,y,30,29,31,已知这组数据的平均数为30,方差为2,则|x-y|的值为
A.1 B.2 C.3 D.4
4.若对任意实数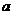 ,函数
,函数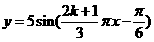
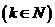 在区间
在区间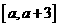 上的值
上的值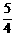 出现不少于4次且不多于8次,则
出现不少于4次且不多于8次,则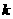 的值为(
)
的值为(
)
A. 2 B. 4 C. 3或4 D. 2或3
3.下列命题不正确的是
A.如果一个平面内的一条直线垂直于另一个平面内的任意直线,则两平面垂直;
B.如果一个平面内的任一条直线都平行于另一个平面,则两平面平行;
C.如果两条不同的直线在一平面内的射影互相垂直,则这两条直线垂直;
D.如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行
2.已知函数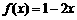 ,若
,若 ,
,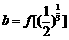 ,
,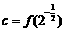 ,则( )
,则( )
A.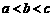 B.
B.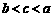 C.
C.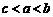 D.
D.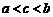
1.设全集为U,若命题p:2011∈A∩B,则命题非p为 ( )
A. 2011∈A∪B B. 2011∉A∪B
C. 2011∈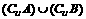 D.
2011∈
D.
2011∈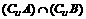
(二)选考题:共10分.请考生从给出的3道题中任选一题做答,并在答题卡上把所选题目的题号打“√”。注意所做题目的题号必须与所打“√”的题号一致,在答题卡选答区域指定位置答题。如果多选,则按所做的第一题计分。
22. (本题满分10分) 选修4-1:几何证明选讲
(本题满分10分) 选修4-1:几何证明选讲
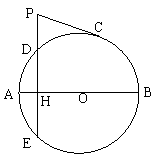
如图,圆O的直径AB=10,弦DE⊥AB于点H, AH=2.
(Ⅰ)求DE的长;
(Ⅱ)延长ED到P,过P作圆O的切线,切点为C,
若PC=2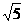 ,求PD的长.
,求PD的长.
23.(本题满分10分) 选修4-4:坐标系与参数方程
已知曲线C1的极坐标方程为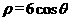 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为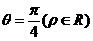 ,曲线C1,C2相交于点A,B.
,曲线C1,C2相交于点A,B.
(Ⅰ)将曲线C1,C2的极坐标方程化为直角坐标方程;
(Ⅱ)求弦AB的长.
24.(本题满分10分) 选修4-5:不等式选讲
(Ⅰ)解关于x的不等式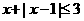 ;
;
(Ⅱ)若关于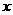 的不等式
的不等式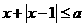 有解,求实数
有解,求实数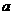 的取值范围.
的取值范围.
(一)必考题:(共9题,共80分)
填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)
13.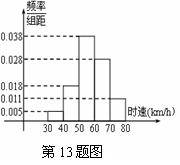 某市内有一条主干路段,为了使行车安全同时也
能增加车流量,规定通过该路段的汽车时速不得
低于40km/h,也不得超过70km/h,否则视为违
规扣分.某天有1000辆汽车经过了该路段,经过
雷达测速得到这些汽车行驶时速的频率分布直方图
如图所示,则违规扣分的汽车大约为 辆.
某市内有一条主干路段,为了使行车安全同时也
能增加车流量,规定通过该路段的汽车时速不得
低于40km/h,也不得超过70km/h,否则视为违
规扣分.某天有1000辆汽车经过了该路段,经过
雷达测速得到这些汽车行驶时速的频率分布直方图
如图所示,则违规扣分的汽车大约为 辆.
14.过原点作曲线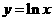 的切线,则切点为___________.
的切线,则切点为___________.
15.在平面几何里,有:“若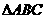 的三边长分别为
的三边长分别为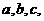 内切圆半径为
内切圆半径为 ,则三角形面积为
,则三角形面积为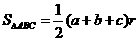 ” .拓展到空间,类比上述结论,“若四面体
” .拓展到空间,类比上述结论,“若四面体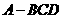 的四个面的面积分别为
的四个面的面积分别为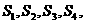 内切球的半径为
内切球的半径为 ,则四面体的体积为
”.
,则四面体的体积为
”.
16.给出下列有关命题的四个说法:
①“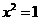 ”是“
”是“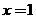 ”的必要不充分条件;
”的必要不充分条件;
②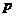 :“
:“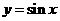 在第一象限是增函数”;
在第一象限是增函数”;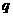 :“
:“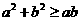 ”;则
”;则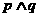 是真命题;
是真命题;
③命题“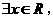 使得
使得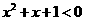 ”的否定是:“
”的否定是:“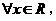 均有
均有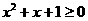 ” ;
” ;
④命题“若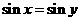 ,则
,则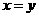 或
或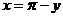 ”的逆否命题为真命题.
”的逆否命题为真命题.
其中说法正确的有 (只填正确的序号).
解答题:(本大题5小题,共60分,解答应写出文字说明、证明过程或演算步骤,并把解答写在答卷纸的相应位置上)
17.(本题满分12分)
在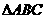 中,
中,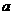 ,
,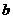 ,
,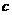 分别为内角
分别为内角 ,
,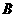 ,
,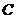 所对的边,且满足
所对的边,且满足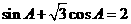 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)现给出三个条件:①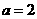 ;②
;②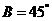 ;③
;③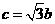 .
.
试从中选出两个可以确定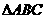 的条件,写出你的选择,并以此为依据求
的条件,写出你的选择,并以此为依据求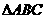 的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分) .
的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分) .
18.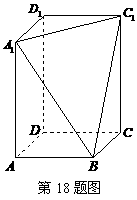 (本题满分12分)
(本题满分12分)
在长方体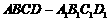 中,
中,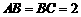 ,过
,过 、
、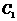 、
、
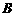 三点的平面截去长方体的一个角后,得到如图所示的几
何体
三点的平面截去长方体的一个角后,得到如图所示的几
何体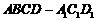 ,且这个几何体的体积为
,且这个几何体的体积为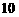 .
(Ⅰ)求棱
.
(Ⅰ)求棱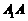 的长;
的长;
(Ⅱ)若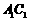 的中点为
的中点为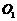 ,求异面直线
,求异面直线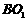 与
与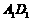 所成角
的余弦值.
所成角
的余弦值.
19.(本题满分12分)
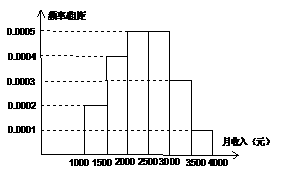
某地统计局就本地居民的月收入调查了 人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组
表示收入在
人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组
表示收入在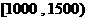 之间).
之间).
(Ⅰ)根据频率分布直方图估计样本
数据的中位数所在的区间;
(Ⅱ)求被调查居民月收入在
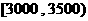 之间的人数;
之间的人数;
(Ⅲ)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这 人中,用分层抽样方法抽出
人中,用分层抽样方法抽出 人作进一步分析,则月收入在
人作进一步分析,则月收入在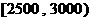 的这段应抽多少人?
的这段应抽多少人?
20.(本题满分12分)
已知椭圆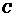 :
: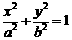 (
(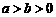 ),其左、右焦点分别为
),其左、右焦点分别为 、
、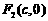 ,且
,且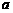 、
、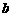 、
、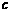 成等比数列.
成等比数列.
(Ⅰ)若椭圆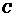 的上顶点、右顶点分别为
的上顶点、右顶点分别为 、
、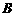 ,求证:
,求证: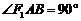 ;
;
(Ⅱ)若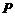 为椭圆
为椭圆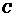 上的任意一点,是否存在过点
上的任意一点,是否存在过点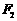 、
、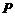 的直线
的直线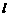 ,使
,使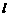 与
与 轴的交点
轴的交点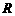 满足
满足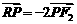 ?若存在,求直线
?若存在,求直线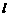 的斜率
的斜率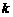 ;若不存在,请说明理由.
;若不存在,请说明理由.
21.(本题满分12分)
已知向量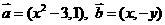 ,(其中实数
,(其中实数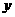 和
和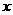 不同时为零),当
不同时为零),当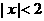 时,
时,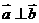 ,当
,当 时,
时,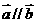 .
.
(Ⅰ) 求函数式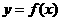 ;
;
(Ⅱ)求函数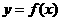 的单调递减区间;
的单调递减区间;
(Ⅲ)若对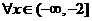
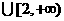 ,都有
,都有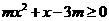 ,求实数
,求实数 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com