
题目列表(包括答案和解析)
6.在等差数列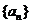 中,有
中,有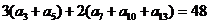 ,则此数列的前13项和为:
,则此数列的前13项和为:
A.24 B.39 C.52 D.104
5. 已知
已知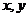 的值如表所示:
的值如表所示:
如果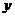 与
与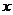 呈线性相关且回归直线方程为
呈线性相关且回归直线方程为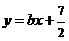 ,则
,则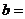
A.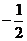 B.
B.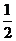 C.
C.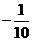 D.
D.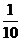
4.在△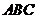 中,
中,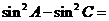
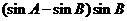 ,则角
,则角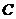 等于
等于
A.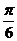 B.
B.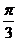 C.
C.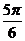 D.
D.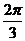
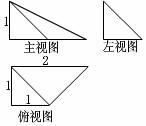
3.一个棱锥的三视图如右图所示,则它的体积为
A.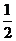 B.
B.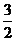
C.1 D.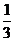
2.条件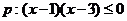 ,条件
,条件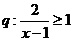 ,则
,则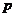 是
是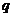 的
的
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
1.复数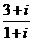 等于
等于
A.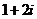 B.
B.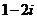 C.
C.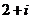 D.
D.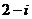
20、(本小题满分16分)
已知函数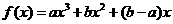 (
(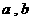 不同时为零的常数),导函数为
不同时为零的常数),导函数为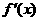 .
.
(1)当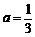 时,若存在
时,若存在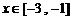 使得
使得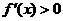 成立,求
成立,求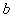 的取值范围;
的取值范围;
(2)求证:函数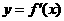 在
在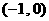 内至少有一个零点;
内至少有一个零点;
(3)若函数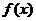 为奇函数,且在
为奇函数,且在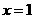 处的切线垂直于直线
处的切线垂直于直线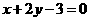 ,
,
关于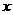 的方程
的方程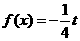 在
在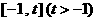 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数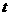 的取值范围.
的取值范围.
19、(本题满分16分)
已知直线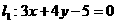 ,圆
,圆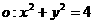 .
.
(1)求直线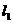 被圆O所截得的弦长;
被圆O所截得的弦长;
(2)如果过点(-1,2)的直线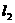 与
与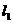 垂直,
垂直,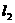 与圆心在直线
与圆心在直线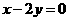 上的圆M相切,圆M被直线
上的圆M相切,圆M被直线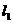 分成两段圆弧,其弧长比为2∶1,求圆M的方程.
分成两段圆弧,其弧长比为2∶1,求圆M的方程.
18、(本小题满分15分)
已知数列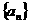 的前n项和为
的前n项和为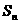 ,
,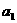 =1,且
=1,且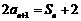
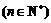 .
.
(1)求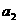 ,
,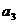 的值,并求数列
的值,并求数列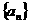 的通项公式;
的通项公式;
(2)解不等式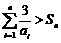
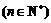 .
.
17、(本小题满分15分)
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本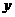 (元)与月处理量
(元)与月处理量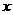 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: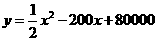 ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com