
题目列表(包括答案和解析)
19. (本小题满分12分)
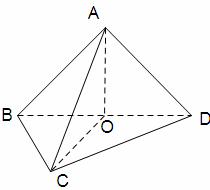
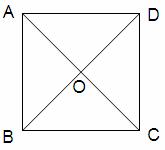
已知正方形ABCD的边长为1,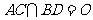 .将正方形ABCD沿对角线
.将正方形ABCD沿对角线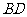 折起,使
折起,使 ,得到三棱锥A-BCD,如图所示.
,得到三棱锥A-BCD,如图所示.
(1)求证: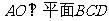 ;
;
(2)求二面角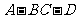 的余弦值.
的余弦值.

18. (本小题满分12分)
某地区举办科技创新大赛,有50件科技作品参赛,大赛组委会对这50件作品分别
从“创新性”和“实用性”两项进行评分,每项评分均按等级采用5分制,若设“创新性”得分为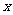 ,“实用性”得分为
,“实用性”得分为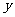 ,统计结果如下表:
,统计结果如下表:
 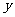 作品数量 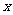 |
实用性 |
|||||
|
1分 |
2分 |
3分 |
4分 |
5分 |
||
|
创 新 性 |
1分 |
1 |
3 |
1 |
0 |
1 |
|
2分 |
1 |
0 |
7 |
5 |
1 |
|
|
3分 |
2 |
1 |
0 |
9 |
3 |
|
|
4分 |
1 |
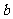 |
6 |
0 |
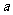 |
|
|
5分 |
0 |
0 |
1 |
1 |
3 |
(1)求“创新性为4分且实用性为3分”的概率;
(2)若“实用性”得分的数学期望为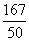 ,求
,求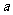 、
、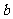 的值.
的值.
17. (本小题满分12分)
已知函数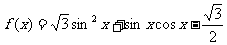
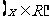 .
.
(1)若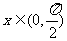 ,求
,求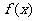 的最大值;
的最大值;
(2)在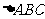 中,若
中,若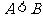 ,
,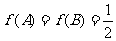 ,求
,求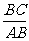 的值
的值
16. 目标函数是单峰函数,若用分数法需要从12个试验点中找出最佳点,则前两个试验点放在因素范围的位置为
15. 已知曲线C的极坐标方程为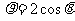 ,则曲线C上的点到直线
,则曲线C上的点到直线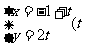 为参数)的距离的最大值为
.
为参数)的距离的最大值为
. 
14.如图,半径为2的⊙O中,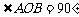 ,
,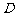 为
为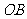 的中点,
的中点,
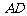 的延长线交⊙O于点
的延长线交⊙O于点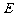 ,则线段
,则线段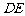 的长为
的长为
13. 在平面直角坐标系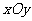 中,
中,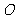 为坐标原点.定义
为坐标原点.定义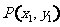 、
、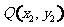 两点之间的“直角距离”为
两点之间的“直角距离”为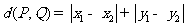 .若点
.若点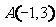 ,则
,则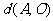 =
;
=
;
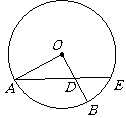 已知点
已知点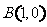 ,点M是直线
,点M是直线 上的动点,
上的动点,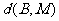 的最小值为 .
的最小值为 .
12. 已知等差数列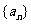 的前n项和为
的前n项和为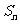 ,若
,若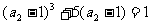 ,
,
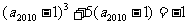 ,则
,则

11. 把边长为1的正方形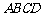 沿对角线
沿对角线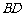 折起形成三棱锥
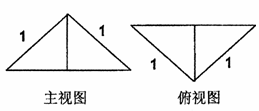
折起形成三棱锥 的主视图与俯视图如图所示,则左视图的面积为
的主视图与俯视图如图所示,则左视图的面积为
10. 如图给出的是计算 的值的程序框图,其中判断框内应填
.
的值的程序框图,其中判断框内应填
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com