
题目列表(包括答案和解析)
23.(本小题满分10分)
选修4-4:极坐标与参数方程:
已知椭圆C的极坐标方程为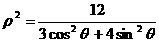 ,点
,点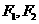 为其左,右焦点,直线
为其左,右焦点,直线 的参数方程为
的参数方程为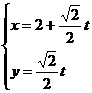 (
(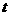 为参数,
为参数,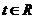 ).
).
(Ⅰ)求直线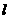 和曲线C的普通方程;
和曲线C的普通方程;
(Ⅱ)求点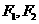 到直线
到直线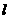 的距离之和.
的距离之和.
22.(本小题满分10分)
 选修4-1:几何证明选讲:
选修4-1:几何证明选讲:
如图,在Rt△ABC中,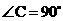 , BE平分∠ABC交AC于点E, 点D在AB上,
, BE平分∠ABC交AC于点E, 点D在AB上,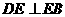 .
.
(Ⅰ)求证:AC是△BDE的外接圆的切线;
(Ⅱ)若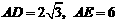 ,求EC的长.
,求EC的长.
21. (本小题满分12分)
已知函数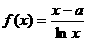 ,其中
,其中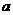 为实数.
为实数.
(1)当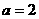 时,求曲线
时,求曲线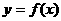 在点
在点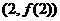 处的切线方程;
处的切线方程;
(2)是否存在实数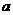 ,使得对任意
,使得对任意 ,
,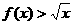 恒成立?若不存在,请说明理由,若存在,求出
恒成立?若不存在,请说明理由,若存在,求出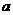 的值并加以证明.
的值并加以证明.
21解:(1)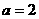 时,
时,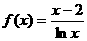 ,
,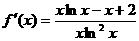 ,--------------------2分
,--------------------2分
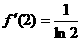 ,又
,又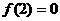 -----------------------------------------3分
-----------------------------------------3分
所以切线方程为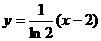 -------------------------------------5分
-------------------------------------5分
(2)1°当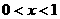 时,
时,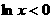 ,则
,则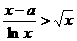
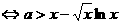
令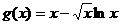 ,
,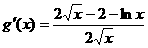 ,
,
再令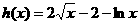 ,
,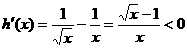
当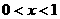 时
时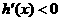 ,∴
,∴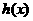 在
在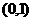 上递减,
上递减,
∴当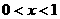 时,
时,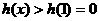 ,
,
∴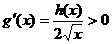 ,所以
,所以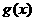 在
在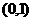 上递增,
上递增,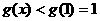 ,
,
所以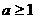 --------------------------------------------8分
--------------------------------------------8分
2°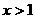 时,
时,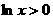 ,则
,则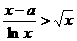
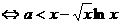
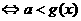
由1°知当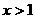 时
时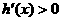 ,
,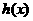 在
在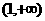 上递增
上递增
当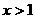 时,
时,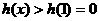 ,
,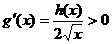
所以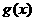 在
在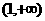 上递增,∴
上递增,∴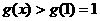
∴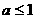 ;------------------------------------------------------11分
;------------------------------------------------------11分
由1°及2°得: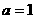 -------------------------------------------12分
-------------------------------------------12分
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分
20. (本小题满分12分)
如图,线段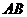 过y轴上一点
过y轴上一点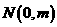 ,
,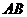 所在直线的斜率为
所在直线的斜率为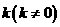 ,两端点
,两端点 、
、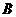 到y轴的距离之差为
到y轴的距离之差为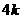 .
.
(Ⅰ)求出以y轴为对称轴,过 、
、 、
、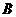 三点的抛物线方程;
三点的抛物线方程;
(Ⅱ)过抛物线的焦点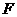 作动弦
作动弦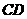 ,过
,过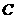 、
、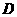 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为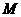 ,求点
,求点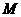 的轨迹方程,并求出
的轨迹方程,并求出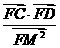 的值.
的值.
19. (本小题满分12分)
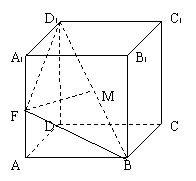 如图,已知棱柱
如图,已知棱柱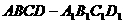 的底面是菱形,且
的底面是菱形,且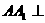 面
面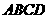 ,
,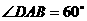 ,
,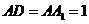 ,
,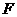 为棱
为棱 的中点,
的中点,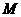 为线段
为线段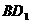 的中点,
的中点,
(Ⅰ)求证: 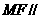 面
面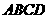 ;
;
(Ⅱ)判断直线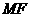 与平面
与平面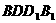 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(Ⅲ)求三棱锥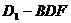 的体积.
的体积.
18. (本小题满分12分)
某大学高等数学老师这学期分别用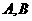 两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
|
|
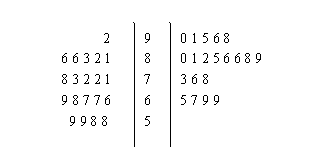

(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的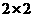 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
|
|
甲班 |
乙班 |
合计 |
|
优秀 |
|
|
|
|
不优秀 |
|
|
|
|
合计 |
|
|
|
下面临界值表仅供参考:
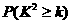 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
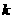 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: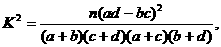 其中
其中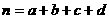 )
)
17. (本小题满分12分)
已知向量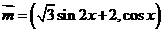 ,
,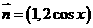 ,设函数
,设函数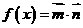 .
.
(1)求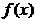 的最小正周期与单调递增区间。
的最小正周期与单调递增区间。
(2)在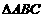 中,
中,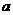 、
、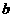 、
、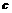 分别是角
分别是角 、
、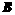 、
、 的对边,若
的对边,若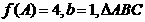 的面积为
的面积为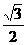 ,求
,求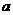 的值。
的值。
16. 已知F1、F2是椭圆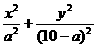 =1(5<a<10)的两个焦点,B是短轴的一个端点,设△F1BF2的面积为
=1(5<a<10)的两个焦点,B是短轴的一个端点,设△F1BF2的面积为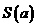 ,则
,则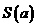 的最大值是
的最大值是
15. 在边长为2的正三角形ABC中,以A为圆心,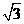 为半径画一弧,分别交AB,AC于D,E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是________.
为半径画一弧,分别交AB,AC于D,E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是________.
14. 若某程序框图如图所示,则该程序运行后输出的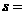 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com