
题目列表(包括答案和解析)
8.设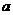 <b,函数
<b,函数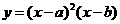 的图像可能是
的图像可能是
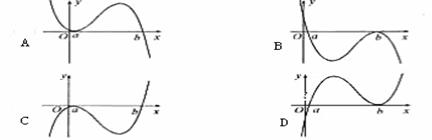
9 设函数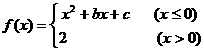 ,若
,若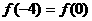 ,
,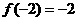 ,则函数
,则函数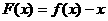 的零点个数为
的零点个数为
A. 1 B. 2 C. 3 D. 4
7.若{ }为等差数列,
}为等差数列,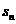 是其前n项的和,且
是其前n项的和,且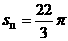 ,则
,则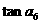 =
=
A.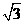 B.
B.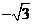 C.
C.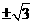 D.
D.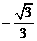
1 已知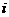 是虚数单位,
是虚数单位, 和
和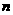 都是实数,且
都是实数,且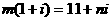 ,则
,则
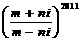 =
=
A.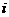 B.
B.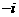 C.
C.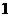 D.
D.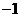
2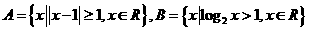 ,则“
,则“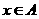 ”是“
”是“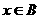 ”的
”的
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分也非必要条件
3 过点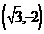 的直线
的直线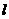 经过圆
经过圆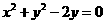 的圆心,则直线
的圆心,则直线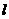 的倾斜角大小为
的倾斜角大小为
A.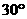 B.
B. C.
C. 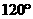 D.
D. 
4 设m,n是两条不同的直线,α、β、γ是三个不同的平面 给出下列四个命题:
①若m⊥α,n∥α,则m⊥n; ②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n; ④若α∥β,β∥γ,m⊥α,,则m⊥γ
其中正确命题的序号是:
A.①和② B.②和③ C.③和④ D.①和④
5 若点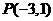 在双曲线
在双曲线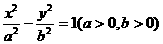 的左准线上,过点
的左准线上,过点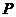 且方向向量为
且方向向量为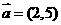 的光线,经直线
的光线,经直线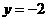 反射后通过双曲线的左焦点,则这个双曲线的离心率为
反射后通过双曲线的左焦点,则这个双曲线的离心率为
A.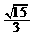 B.
B.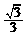 C.
C.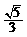 D.
D.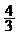
6.直线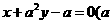 是常数),当此直线在
是常数),当此直线在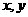 轴的截距和最小时,正数
轴的截距和最小时,正数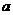 的值是
的值是
A.0
B.2
C.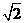 D.1
D.1
21.(本题满分14分)
已知函数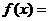
 ,
,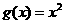 ,记
,记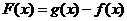
(Ⅰ)求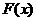 的单调区间;
的单调区间;
(Ⅱ)当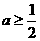 时,若
时,若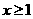 ,比较:
,比较: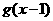 与
与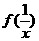 的大小;
的大小;
(Ⅲ)若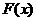 的极值为
的极值为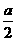 ,问是否存在实数
,问是否存在实数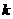 ,使方程
,使方程
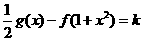 有四个不同实数根?若存在,求出实数
有四个不同实数根?若存在,求出实数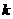 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
20. (本题满分13分)
(本题满分13分)
如图所示,在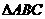 中,
中,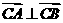 ,
,
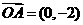 ,
,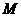 在
在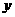 轴上,
轴上,
且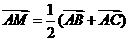 ,
,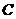 在
在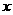 轴上移动。
轴上移动。
(Ⅰ)求点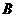 的轨迹
的轨迹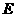 的方程;
的方程;
(Ⅱ)过点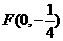 的直线
的直线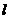 交轨迹
交轨迹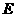 于
于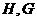 两点(
两点(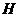 在
在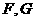 之间),若
之间),若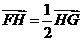 ,求直线
,求直线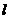 的斜率;
的斜率;
19.(本题满分12分)
已知等差数列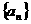 的公差大于0,且
的公差大于0,且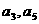 是方程
是方程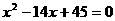 的两根,数列
的两根,数列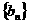 的前
的前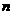 项和为
项和为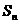 ,且
,且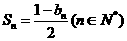 .
.
(Ⅰ) 求数列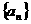 ,
,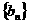 的通项公式;
的通项公式;
(Ⅱ) 记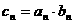 ,求数列
,求数列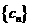 的前
的前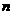 项和
项和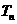 .
.
18.(本题满分12分)
如图,四棱锥P-ABCD的底面是平行四边形,PA⊥平面ABCD,
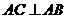 ,
,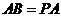 ,点
,点 是
是 上的点,且
上的点,且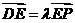 (0
(0
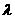
 1).
1).
 (Ⅰ) 求证:PB⊥AC;
(Ⅰ) 求证:PB⊥AC;
(Ⅱ) 求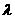 的值,使
的值,使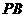 ∥平面
∥平面 ;
;
(Ⅲ)当 时,求二面角
时,求二面角
 的大小.
的大小.
17.(本题满分12分)
某种项目的射击比赛,开始时选手在距离目标100m处射击,若命中则记3分,且停止射击.若第一次射击未命中,可以进行第二次射击,但需在距离目标150m处,这时命中目标记2分,且停止射击.若第二次仍未命中,还可以进行第三次射击,此时需在距离目标200m处,若第三次命中则记1分,并停止射击.若三次都未命中则记0分,并停止射击.已知选手甲的命中率与目标的距离的平方成反比,他在100m处击中目标的概率为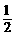 ,且各次射击都相互独立.
,且各次射击都相互独立.
(Ⅰ)求选手甲在三次射击中命中目标的概率;
(Ⅱ)设选手甲在比赛中的得分为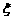 ,求
,求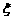 的分布列和数学期望.
的分布列和数学期望.
16.(本题满分12分)
在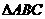 中,设
中,设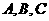 的对边分别为
的对边分别为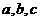 ,向量
,向量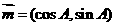 ,
,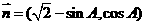 ,且
,且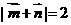 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若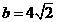 ,
, ,求
,求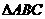 的面积.
的面积.
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
A.(不等式选做题)不等式 的解集是
.
的解集是
.
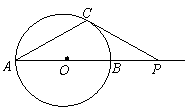 B. (几何证明选做题) 如图,
B. (几何证明选做题) 如图,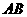 是⊙
是⊙ 的直径,
的直径,
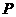 是
是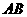 延长线上的一点,过
延长线上的一点,过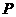 作⊙
作⊙ 的切线,
的切线,
切点为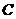 ,
,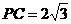 ,若
,若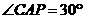 ,
,
则⊙ 的直径
的直径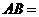 .
.
C. (极坐标系与参数方程选做题)若圆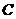 :
: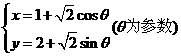 与直线
与直线 相切,则
相切,则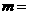 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com