
题目列表(包括答案和解析)
3.现有 个数,其平均数是
个数,其平均数是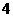 ,且这
,且这 个数的平方和是
个数的平方和是 ,那么这个数组的标准差是
,那么这个数组的标准差是
A.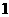 B.
B.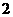 C.
C.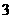 D.
D.
2.已知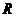 是实数集,
是实数集,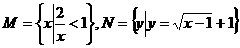 ,则
,则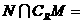
A.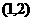 B.
B.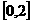 C.
C.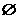 D.
D.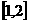
1.复数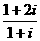 (
(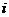 是虚数单位)的虚部是
是虚数单位)的虚部是
A.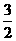 B.
B.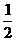 C.
C.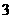 D.
D.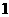
22. (本题满分14分)设函数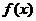
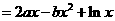 .给出下列条件,条件A:
.给出下列条件,条件A: 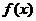 在
在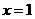 和
和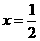 处取得极值;条件
处取得极值;条件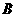 :
: 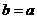
(Ⅰ)在A条件下,求出实数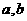 的值;
的值;
(Ⅱ) 在A条件下,对于在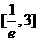 上的任意
上的任意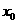 ,不等式
,不等式 恒成立,求实数
恒成立,求实数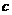 的最小值;
的最小值;
(Ⅲ) 在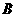 条件下, 若
条件下, 若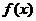 在
在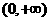 上是单调函数,求实数
上是单调函数,求实数 的取值范围.
的取值范围.
21.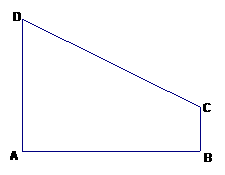 (满分12分)如图,在直角梯形
(满分12分)如图,在直角梯形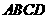 中,
中,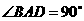 ,
,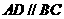 ,
,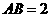 ,
,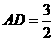 ,
,
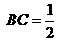 ,椭圆以
,椭圆以 、
、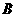 为焦点且经过点
为焦点且经过点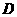 .
.
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(Ⅱ)以该椭圆的长轴为直径作圆,判断点C与该圆的位置关系。
20. (本题满分12分)已知等差数列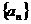 的公差大于0,且
的公差大于0,且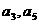 是方程
是方程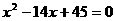 的两根,数列
的两根,数列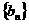 的前
的前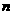 项的和为
项的和为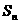 ,且
,且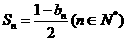 .
.
(Ⅰ) 求数列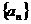 ,
,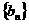 的通项公式;
的通项公式;
(Ⅱ) 记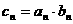 ,求证:
,求证: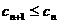 ;(Ⅲ)求数列
;(Ⅲ)求数列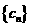 的前
的前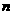 项和.
项和.
19.(本题满分12分)如图,已知三棱锥A-BPC中,AP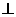 PC.AC
PC.AC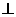 BC.M为AB中点.D为PB中点.且△PMB为正三角形.
BC.M为AB中点.D为PB中点.且△PMB为正三角形.
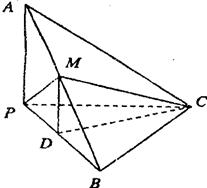 (1)求证:DM//平面APC;
(1)求证:DM//平面APC;
(2)求证:平面ABC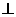 平面APC;
平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM体积
18. (本题满分12分)为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行出样检查,测得身高情况的统计图如下:
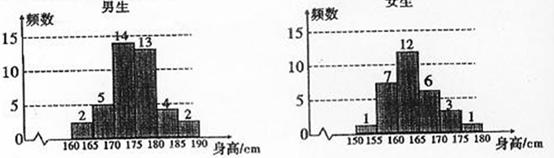
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
17.(本题满分12分)已知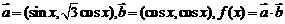 。
。
(1)若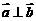 ,求
,求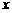 的取值集合;(2)求函数
的取值集合;(2)求函数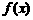 的周期及增区间。
的周期及增区间。
16、设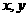 满足约束条件
满足约束条件 ,
,
若目标函数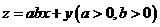 的最大值为8,则
的最大值为8,则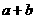 的最小值为____▲____
的最小值为____▲____
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com