
题目列表(包括答案和解析)
1、设集合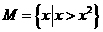 ,
,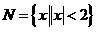 ,则( )
,则( )
A.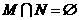 B.
B.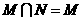 C.
C.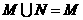 D.
D.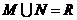
21.(本小题满分14分)己知函数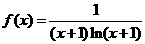 .
.
(1) 求函数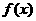 的定义域;(2) 求函数
的定义域;(2) 求函数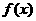 的增区间;
的增区间;
(3) 是否存在实数 ,使不等式
,使不等式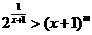 在
在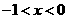 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
20.(本小题满分14分)已知圆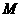 :
: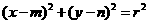 及定点
及定点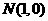 ,点
,点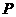 是圆
是圆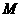 上的动点,点
上的动点,点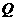 在
在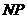 上,点
上,点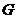 在
在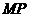 上,
上,
且满足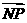 =2
=2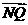 ,
,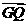 ·
·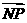 =
= .
.
(1)若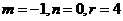 ,求点
,求点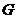 的轨迹
的轨迹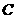 的方程;
的方程;
(2)若动圆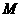 和(1)中所求轨迹
和(1)中所求轨迹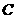 相交于不同两点
相交于不同两点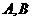 ,是否存在一组正实数
,是否存在一组正实数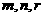 ,使得直线
,使得直线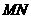 垂直平分线段
垂直平分线段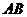 ,若存在,求出这组正实数;若不存在,说明理由.
,若存在,求出这组正实数;若不存在,说明理由.
19.(本小题满分14分)过点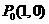 作曲线
作曲线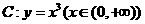 的切线,切点为
的切线,切点为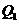 ,过
,过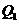 作
作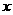 轴的垂线交
轴的垂线交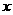 轴于点
轴于点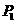 ,又过
,又过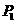 作曲线C的,切点为
作曲线C的,切点为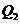 ,过
,过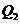 作
作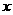 轴的垂线交
轴的垂线交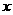 轴于点
轴于点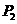 ,…,依次下去得到一系列点
,…,依次下去得到一系列点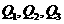 ,…,设点
,…,设点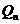 的横坐标为
的横坐标为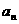 .(1)求数列
.(1)求数列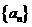 的通项公式;
的通项公式;
(2)求和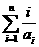 ;(3)求证:
;(3)求证: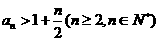 .
.
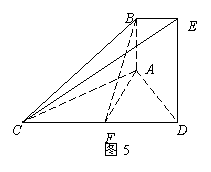
18.(本小题满分14分)如图5,已知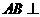 平面
平面 ,
,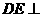 平面
平面 ,△
,△ 为等边三角形,
为等边三角形,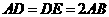 ,
,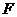 为
为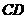 的中点.
的中点.
(1)求证: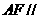 平面
平面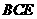 ;(2)求证:平面
;(2)求证:平面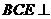 平面
平面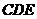 ;
;
 (3)求直线
(3)求直线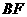 和平面
和平面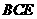 所成角的正弦值.
所成角的正弦值.
17.(本小题满分12分)第16届亚运会将于2010年11月在广州市举行,射击队运动员们正在积极备战. 若某运动员每次射击成绩为10环的概率为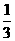 . 求该运动员在5次射击中,(1)恰有3次射击成绩为10环的概率;
. 求该运动员在5次射击中,(1)恰有3次射击成绩为10环的概率;
(2)至少有3次射击成绩为10环的概率;
(3)记“射击成绩为10环的次数”为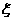 ,求
,求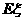 .(结果用分数表示)
.(结果用分数表示)
证明过程和演算步骤.
16.(本小题满分12分)已知平面上三点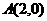 ,
,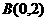 ,
,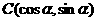 .
.
(1)若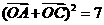 (O为坐标原点),求向量
(O为坐标原点),求向量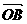 与
与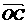 夹角的大小;
夹角的大小;
(2)若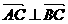 ,求
,求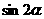 的值.
的值.
(二)选做题(14-15题,考生只能从中选做一题)
14.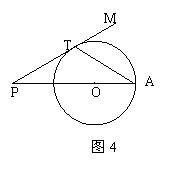 (几何证明选讲选做题)如图4,
(几何证明选讲选做题)如图4,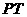 为圆
为圆 的切线,
的切线,
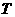 为切点,
为切点,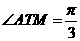 ,圆
,圆 的面积为
的面积为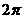 ,则
,则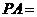 .
.
15.(坐标系与参数方程选做题)在极坐标系中,
曲线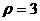 截直线
截直线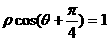 所得的弦长为 .
所得的弦长为 .
(一)必做题(9-13题)
9.在二项式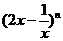 的展开式中,若第
的展开式中,若第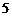 项是常数项,则
项是常数项,则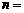 _______.
_______.
(用数字作答)
10.已知等差数列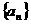 中,有
中,有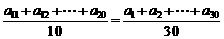 成立.
成立.
 类似地,在等比数列
类似地,在等比数列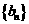 中,
中,
有_____________________成立.
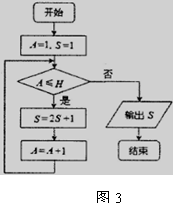
11.按如图3所示的程序框图运行程序后,
输出的结果是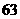 ,
,
则判断框中的整数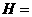 _________.
_________.
12.设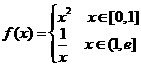 ,则
,则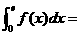 _____.
_____.
13.在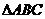 中,
中,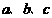 分别为内角
分别为内角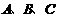 所对的边,且
所对的边,且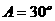 .
.
现给出三个条件:①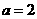 ; ②
; ②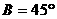 ;③
;③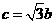 .试从中选出两个可以确定
.试从中选出两个可以确定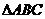 的条件,并以此为依据求
的条件,并以此为依据求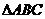 的面积.(只需写出一个选定方案即可)你选择的条件是
(用序号填写);由此得到的
的面积.(只需写出一个选定方案即可)你选择的条件是
(用序号填写);由此得到的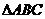 的面积为
.
的面积为
.
8.若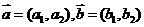 ,定义一种向量积:
,定义一种向量积: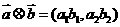 ,
,
已知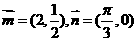 ,且点
,且点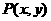 在函数
在函数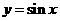 的图象上运动,点
的图象上运动,点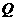 在函数
在函数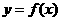 的图象上运动,且点
的图象上运动,且点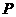 和点
和点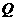 满足:
满足: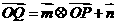 (其中O为坐标原点),则函数
(其中O为坐标原点),则函数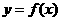 的最大值
的最大值 及最小正周期
及最小正周期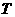 分别为?网 ☆
分别为?网 ☆
A.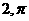 B.
B.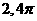 C.
C.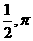 D.
D.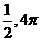
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com