
题目列表(包括答案和解析)
22.(本小题满分14分)
如图,已知椭圆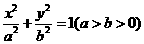 的左、右焦点分别为
的左、右焦点分别为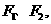 短轴两的端点为A、B,且四边形
短轴两的端点为A、B,且四边形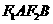 是边长为2的正方形.
是边长为2的正方形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若C、D分别是椭圆长轴的左、右端点,动点M满足MD 连结
连结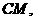 交椭圆于点
交椭圆于点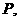 证明:
证明: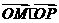 为定值;
为定值;
(Ⅲ)在(Ⅱ)的条件下,试问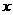 轴上是否存在异于点
轴上是否存在异于点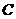 的定点
的定点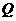 ,使得以
,使得以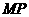 为直径的圆恒过直线
为直径的圆恒过直线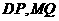 的交点,若存在,求出点
的交点,若存在,求出点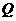 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
21.(本小题满分12分)
已知函数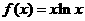 .
.
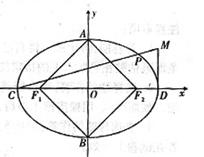
(Ⅰ)若直线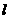 过点
过点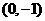 ,并且与曲线
,并且与曲线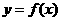 相切,求直线
相切,求直线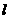 的方程;
的方程;
 (Ⅱ)设函数
(Ⅱ)设函数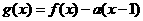 ,其中
,其中 ,求函数
,求函数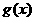 在区间
在区间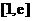 上的最小值.(其中
上的最小值.(其中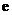 为自然对数的底数)
为自然对数的底数)
20. (本小题满分12分)
(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面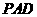 ⊥底面ABCD,Q为AD的中点,M是PC的中点,
⊥底面ABCD,Q为AD的中点,M是PC的中点,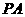 =PD,BC=
=PD,BC=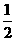 AD.
AD.
(Ⅰ)求证: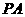
 平面BMQ;
平面BMQ;
(Ⅱ)求证:平面PQB⊥平面PAD.
19.(本小题满分12分)
车间将 名技工平均分为甲、乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
名技工平均分为甲、乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
|
|
1号 |
2号 |
3号 |
4号 |
5号 |
|
甲组 |
4 |
5 |
7 |
9 |
10 |
|
乙组 |
5 |
6 |
7 |
8 |
9 |
(Ⅰ)别求出甲、乙两组技工在单位时间内完成合成合格零件的平均数及方差,并由此比较两组技工的技术水平;
(Ⅱ)质检部门从该车间甲、乙两组中各随机抽取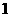 名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过
名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过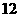 件,则称该车间“质量合格”,求该车间“质量合格”的概率.
件,则称该车间“质量合格”,求该车间“质量合格”的概率.
18.(本小题满分12分)
已知各项都不相等的等差数列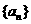 的前6项和为60,且
的前6项和为60,且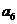 为
为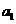 和
和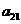 的等比中项.
(I ) 求数列
的等比中项.
(I ) 求数列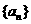 的通项公式;
的通项公式;
(II) 若数列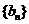 满足
满足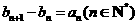 ,且
,且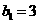 ,求数列
,求数列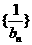 的前
的前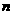 项和
项和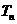 .
.
17.(本小题满分12分)
在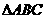 中,
中,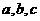 分别是角
分别是角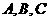 的对边,向量
的对边,向量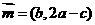 ,
,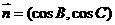 ,且
,且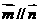 .
.
(Ⅰ)求角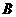 的大小;
的大小;
(Ⅱ)设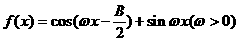 ,且
,且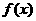 的最小正周期为
的最小正周期为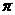 ,求
,求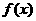 在区间
在区间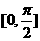 上的最大值和最小值.
上的最大值和最小值.
16.一个三角形数阵如下:
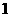
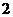
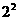
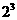
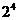
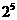
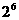
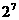
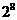
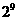
……
按照以上排列的规律,第n 行(n ≥3)从左向右的第3个数为________.
15. 对某学校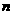 名学生的体重进行统计,得到频率分布直方图如图所示,则体重在75kg以上的学生人数为64人,则
名学生的体重进行统计,得到频率分布直方图如图所示,则体重在75kg以上的学生人数为64人,则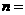 _______.
_______.
14.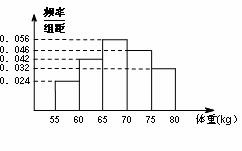 已知
已知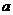 ,
,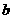 ,
,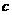 成等差数列,则直线
成等差数列,则直线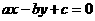 被曲线
被曲线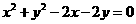 截得的弦长的最小值为_______.
截得的弦长的最小值为_______.
13. 复数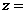
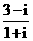 ,则
,则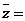 ________.
________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com