
题目列表(包括答案和解析)
7.已知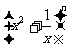 的展开式的各项系数和为32,则展开式中
的展开式的各项系数和为32,则展开式中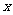 的系数为
的系数为
 A.5
B.10 C.20
D.40
A.5
B.10 C.20
D.40
5.若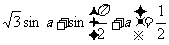 ,则
,则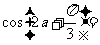
A.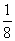 B.
B.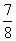 C.
C. 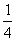 D.
D. 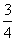
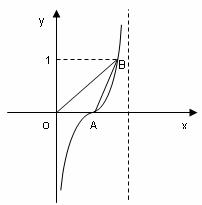
|
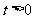 ,若
,若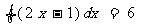 ,则
,则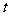 的值等于
的值等于
A.2 B.3 C.6 D.8
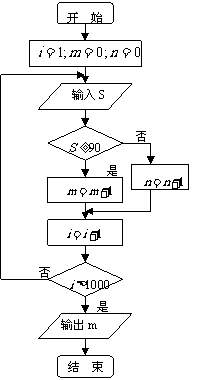
4.右图是统计高三年级1000名同学某次数学考试成绩的程序框图,若输出的结果是720,则这次考试数学分数不低于90分的同学的频率是
A.0.28 B.0.38 C.0.72 D.0.62
3.已知圆锥的母线长为2,母线与底面所成的角为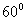 ,则该圆锥的表面积等于
,则该圆锥的表面积等于
A.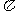 B.
B. 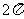 C.
C. 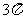 D.
D.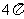
2.圆心在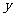 轴上,半径为1,且过点(1,2)的圆的方程是
轴上,半径为1,且过点(1,2)的圆的方程是
 A.
A.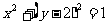 B.
B.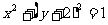
C.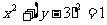 D.
D.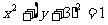
1.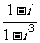 =
=
A.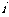 B.
B. C.
C.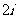 D.
D.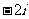
23、解:⑴设选手甲任答一题,正确的概率为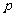 ,依题意
,依题意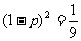 ,
,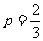 ,
,
甲选答3道题目后进入决赛的概率为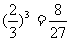 ,甲选答4道、5道题目后进入决赛的概率分别为
,甲选答4道、5道题目后进入决赛的概率分别为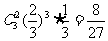 、
、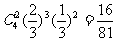 ,所以,选手甲可进入决赛的概率
,所以,选手甲可进入决赛的概率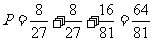 ……………………5分.
……………………5分.
⑵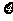 可取3,4,5,依题意
可取3,4,5,依题意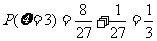 ,
,
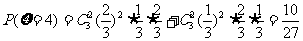 ,
,
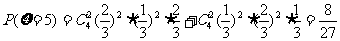 ……7分,
……7分,
(或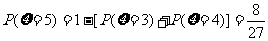 ……7分)
……7分)
所以,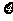 的分布列为:
的分布列为:
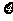
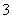
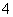
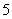
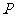
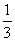
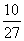
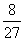
……8分
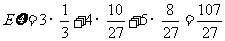 ……10分.
……10分.
20.解:(1)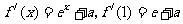 ,所以在
,所以在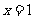 处的切线为
处的切线为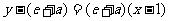
即: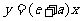 ………………………………2分
………………………………2分
与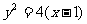 联立,消去
联立,消去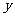 得
得 ,
,
由 知,
知,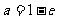 或
或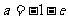 . ………………………………4分
. ………………………………4分
(2)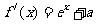
①当 时,
时,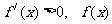 在
在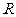 上单调递增,且当
上单调递增,且当 时,
时,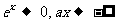 ,
,
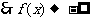 ,故
,故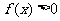 不恒成立,所以
不恒成立,所以 不合题意 ;………………6分
不合题意 ;………………6分
②当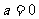 时,
时,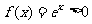 对
对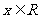 恒成立,所以
恒成立,所以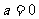 符合题意;
符合题意;
③当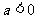 时令
时令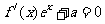 ,得
,得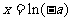 , 当
, 当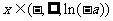 时,
时,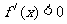 ,
,
当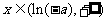 时,
时,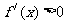 ,故
,故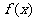 在
在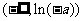 上是单调递减,在
上是单调递减,在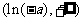 上是单调递增, 所以
上是单调递增, 所以 又
又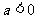 ,
,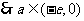 ,
,
综上: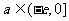 .
………………………………10分
.
………………………………10分
(3)当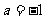 时,由(2)知
时,由(2)知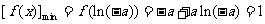 ,
,
设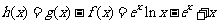 ,则
,则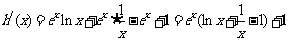 ,
,
假设存在实数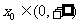 ,使曲线
,使曲线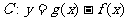 在点
在点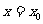 处的切线斜率与
处的切线斜率与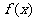 在
在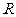 上的最小值相等,
上的最小值相等,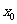 即为方程的解,………………………………13分
即为方程的解,………………………………13分
令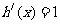 得:
得: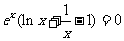 ,因为
,因为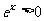 , 所以
, 所以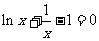 .
.
令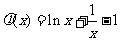 ,则
,则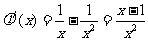 ,
,
当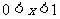 是
是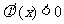 ,当
,当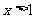 时
时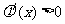 ,所以
,所以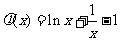 在
在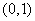 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,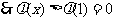 ,故方程
,故方程 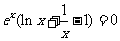 有唯一解为1,
有唯一解为1,
所以存在符合条件的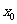 ,且仅有一个
,且仅有一个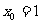 . ………………………………16分
. ………………………………16分
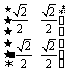
 =
=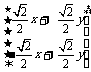 =
= ………………………2分
………………………2分
得到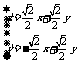 ,得到
,得到 代入
代入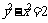 ,得
,得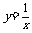 ………………………5分
………………………5分
(2)(法一)曲线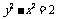 的焦点坐标是
的焦点坐标是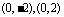 ,渐近线方程
,渐近线方程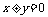 ,
,

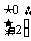 =
=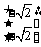

 =
=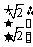 ,………………………
7分
,………………………
7分
设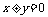 上任意点
上任意点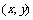 变换后对应的点为
变换后对应的点为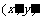

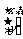 =
= ,得
,得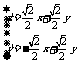 ,求得
,求得 代入
代入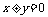 ,得到
,得到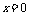 和
和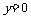 ……………9分
……………9分
矩阵变换后,曲线 的焦点坐标是
的焦点坐标是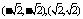 。曲线
。曲线 的渐近线方程为
的渐近线方程为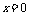 和
和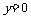 。…………10分
。…………10分
(法二)曲线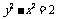 的焦点坐标是
的焦点坐标是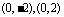 ,渐近线方程
,渐近线方程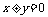 ,
,
将点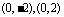 分别代入
分别代入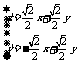 ,得到
,得到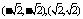 ………………………7分
………………………7分
将 代入
代入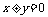 ,得到
,得到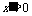 和
和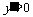 ;………………………9分
;………………………9分
矩阵变换后,曲线 的焦点坐标是
的焦点坐标是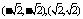 。曲线
。曲线 的渐近线方程为
的渐近线方程为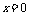 和
和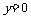 。
。
C.解:设直线为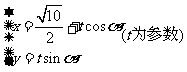 ,代入曲线并整理得
,代入曲线并整理得
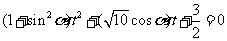 .
.
设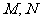 分别对应与
分别对应与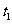 ,
,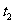 ,则
,则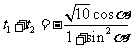 ,
,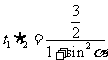 .…………4分
.…………4分
⑴若点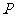 恰为弦
恰为弦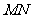 的中点,则
的中点,则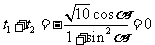 ,∴
,∴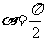 .
.
此时,直线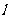 的方程为
的方程为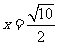 .………………………………………………………7分
.………………………………………………………7分
⑵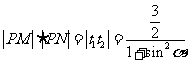 ,
,
当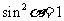 时,即
时,即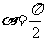 ,
,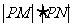 的最小值为
的最小值为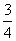 ,此时
,此时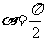 .………………10分
.………………10分
D. 证明: ∵a、b、c均为实数.
∴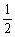 (
(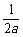 +
+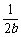 )≥
)≥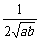 ≥
≥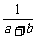 ,当a=b时等号成立;
,当a=b时等号成立;
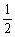 (
(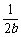 +
+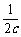 )≥
)≥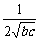 ≥
≥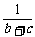 ,当b=c时等号成立;
,当b=c时等号成立;
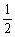 (
(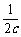 +
+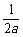 )≥
)≥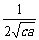 ≥
≥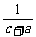 . ………………………………………………7分
. ………………………………………………7分
三个不等式相加即得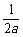 +
+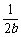 +
+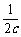 ≥
≥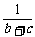 +
+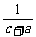 +
+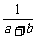 ,
,
当且仅当a=b=c时等号成立. ………………………………………………………10分22、以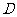 为原点,
为原点,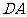 、
、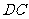 、
、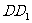 所在直线分别为
所在直线分别为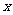 轴、
轴、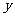 轴、
轴、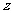 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则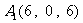 、
、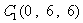 ,设
,设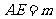 ,则
,则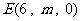 ,
,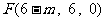 ,从而
,从而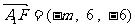 、
、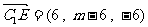 ,直接计算知
,直接计算知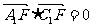 ,所以
,所以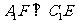 …………4分.
…………4分.
⑵①当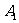 、
、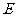 、
、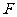 、
、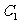 共面时,因为底面
共面时,因为底面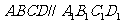 ,所以
,所以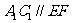 ,所以
,所以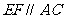 ,从而
,从而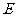 、
、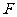 分别是
分别是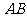 、
、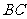 的中点……7分,设
的中点……7分,设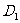 到直线
到直线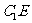 的距离为
的距离为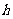 ,在
,在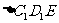 中,
中,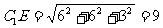 ,
,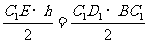 ,
,
解得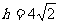 ……7分.
……7分.
②由①得,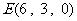 、
、 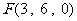 ,设平面
,设平面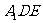 的一个法向量为
的一个法向量为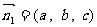 ,依题意
,依题意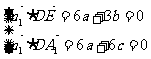 ,所以
,所以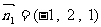 ,同理平面
,同理平面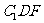 的一个法向量为
的一个法向量为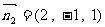 ,由图知,面
,由图知,面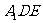 与面
与面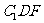 所成二面角的余弦值
所成二面角的余弦值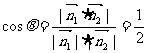 (即
(即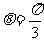 )……10分.
)……10分.
19.解:(1)因为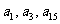 成等比数列,所以
成等比数列,所以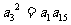 ,即
,即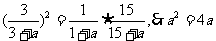 ,
,
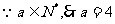 .
……………………5分
.
……………………5分
(2)若存在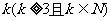 ,使得
,使得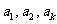 成等差数列,则有
成等差数列,则有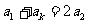 ,
,
即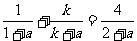 ,得
,得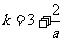 ,
,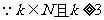 ,
,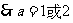 . …………8分
. …………8分
故存在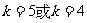 ,使得
,使得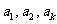 成等差数列,
成等差数列,
且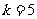 时,
时,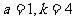 时,
时,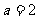 .
………11分
.
………11分
(3)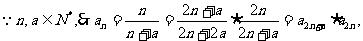 ………13分
………13分
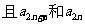 是数列
是数列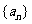 的不同于
的不同于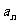 的两项,
的两项,
所以数列中的任意一项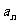 总可以表示成数列中其它两项之积. ……………16分
总可以表示成数列中其它两项之积. ……………16分
18.解:(1)由题意,甲厂排放的污水在流到乙厂时有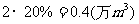 被净化,
被净化,
所以河流在经过乙厂后污水的总含量为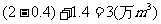 .
.
故河流在经过乙厂后污水含量的百分比约是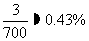 .…………………………6分
.…………………………6分
(2)设甲、乙两厂每天分别处理污水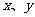 万
万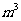 ,两厂处理污水的总费用为
,两厂处理污水的总费用为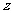 元.
元.
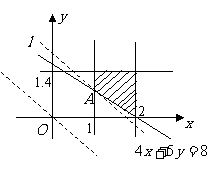 则
则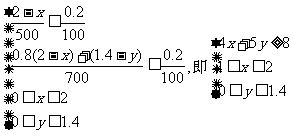 . 目标函数为
. 目标函数为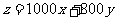 .……………………98分
.……………………98分
作可行域,如图. …………………………11分
平移直线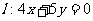 ,当直线经过点
,当直线经过点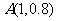 时,
时,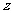 取最小值,
取最小值,
此时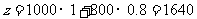 (元)
…………………………13分
(元)
…………………………13分
故甲、乙两厂每天应分别处理1万 、0.8万
、0.8万 污水,才能使两厂处理污水的总费用最小,且最小总费用是1640元.
…………………………15分
污水,才能使两厂处理污水的总费用最小,且最小总费用是1640元.
…………………………15分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com